Взаимодействия среды

Функция чувствительна к переменной окружения ORDER, который определяет количество по умолчанию условий в последовательных расчетах.

Пример 1

Мы вычисляем последовательное расширение sin (x) вокруг x = 0. Результатом является Ряд Тейлора:

s := series(sin(x), x)

Синтаксически, результатом является объект доменного типа Series::Puiseux:

domtype(s)

Математический тип последовательного расширения может быть запрошен с помощью выражения типа Type::Series:

testtype(s, Type::Series(Taylor))

Различные системные функции перегружаются, чтобы работать с серийными объектами. Например, функциональный coeff может использоваться, чтобы извлечь коэффициенты последовательного расширения:

coeff(s, 5)

Стандартные арифметические операторы могут использоваться, чтобы добавить или умножить последовательные расширения:

s + 2*s, s*s

delete s:

Пример 2

Этот пример вычисляет состав s отдельно, т.е. последовательное расширение sin (sin (x)).

s := series(sin(x), x): s @ s = series(sin(sin(x)), x)

delete s:

Пример 3

Мы вычисляем последовательное расширение функции тангенса вокруг источника двумя способами:

series(sin(x), x) / series(cos(x), x) = series(tan(x), x)

bool(%)

Пример 4

Мы вычисляем расширение Лорана вокруг точки 1:

s := series(1/(x^2 - 1), x = 1)

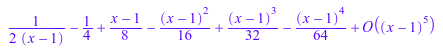
testtype(s, Type::Series(Taylor)),
testtype(s, Type::Series(Laurent))

Пример 5

Без дополнительного аргумента или с опцией Undirected, sign функция не расширена:

series(x*sign(x^2 + x), x) =
series(x*sign(x^2 + x), x, Undirected)

Некоторое упрощение происходит, если вы запрашиваете расширение, которое допустимо вдоль вещественной оси только:

series(x*sign(x^2 + x), x, Real)

sign исчезает от результата, если вы запрашиваете одностороннее расширение вдоль вещественной оси:

series(x*sign(x^2 + x), x, Right),
series(x*sign(x^2 + x), x, Left)

Пример 6

В MuPAD^®, heaviside функция задана только на вещественной оси. Таким образом неориентированное расширение в комплексной плоскости не целесообразно:

series(x*heaviside(x + 1), x)

Warning: Unable to find an undirected series expansion. Try the 'Left', 'Right', or 'Real' option. [Series::main]

После определения соответствующих опций система вычисляет расширение вдоль вещественной оси:

series(x*heaviside(x + 1), x, Real),
series(x*heaviside(x + 1), x, Right)

В точке I в комплексной плоскости, функциональном heaviside не задан, и ни один не последовательное расширение:

series(heaviside(x), x = I, Real)

Пример 7

Мы вычисляем последовательные расширения вокруг бесконечности:

s1 := series((x + 1)/(x - 1), x = complexInfinity)

s2 := series(psi(x), x = infinity)

domtype(s1), domtype(s2)

Несмотря на то, что оба расширения имеют доменный тип Series::PuiseuxS2 не ряд Пюизе в математическом смысле, поскольку первый срок содержит логарифм, который имеет существенную сингулярность в бесконечности:

testtype(s1, Type::Series(Puiseux)),
testtype(s2, Type::Series(Puiseux))

coeff(s2)

Следующее расширение имеет доменный тип Series::gseries:

s3 := series(exp(x)/(1 - x), x = infinity, 4)

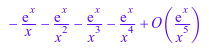
domtype(s3)

delete s1, s2, s3:

Пример 8

Колебание, но ограниченные функции может появиться в “коэффициентах” последовательного расширения также:

s := series(sin(x + 1/x), x = infinity)

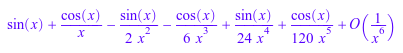
domtype(s), testtype(s, Type::Series(Puiseux))

coeff(s, -1)

Пример 9

Алгебраическое уравнение y ⁵ - y - x = 0 не может быть разрешено в терминах радикалов:

solve(y^5 - y - x, y)

Однако series может вычислить все серийные решения этого уравнения вокруг x = 0:

series(%, x = 0)

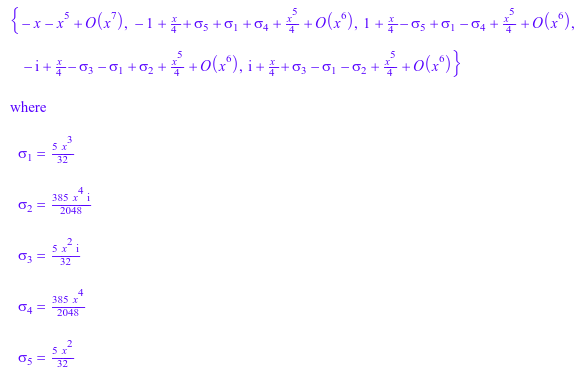
Это может произойти, что сами серийные решения выражаются в терминах RootOfs:

series(RootOf(y^5 -(x + 2*x^2)*y^3 - x^3*y^2
              + (x^3 + x^4)*y + x^4 + x^5, y), x)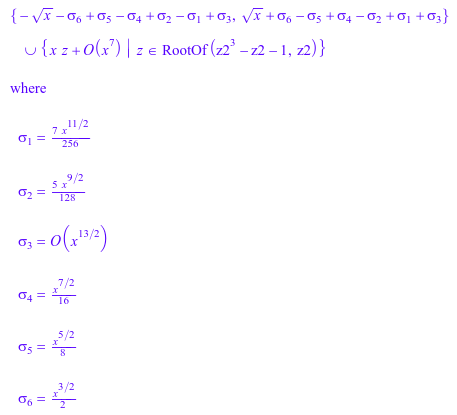

Коэффициентам алгебраического уравнения позволяют быть трансцендентальными. Они внутренне преобразованы в ряд Пюизе series:

series(RootOf(y^3 - y - exp(x - 1) + 1, y), x = 1, 4)

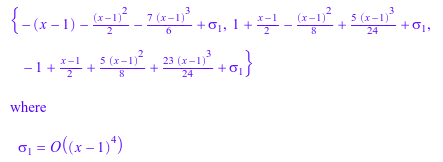
Ошибка происходит, если некоторый коэффициент не может быть расширен в ряд Пюизе:

series(RootOf(y^3 - y - exp(x), y), x = infinity)

Error: Unable to expand coefficients of 'RootOf(y^3 - y - exp(1/x), y)' into a series. [Series::algebraic]

Пример 10

В этом примере мы вычисляем формулу для n-th коэффициент a _n в Разложении Тейлора функции вокруг нуля путем определения infinity как order. Результатом является символьная сумма:

series(exp(-x), x, infinity)

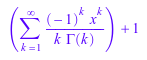
Если вход является многочленным выражением, то так выход:

series(x^5 - 1, x = 1, infinity)

Пример 11

Никакое асимптотическое расширение не существует для функции Бесселя Дж незаданного индекса и series возвращает символьный вызов функции:

series(besselJ(k, x), x=infinity)

domtype(%), type(%)

Пример 12

Разрез логарифма и квадратного корня является отрицательной вещественной осью. Для последовательного расширения на разрезе, series использует функциональный signIm чтобы возвратить расширение, которое допустимо в открытом диске вокруг точки расширения:

series(ln(x), x = -1, 3)

series(sqrt(x), x = -1, 3)

Ситуация более сложна, когда точка расширения является точкой разветвления. Следующее расширение функционального arcsin(x + 1) допустимо в открытом диске вокруг точки разветвления 0:

series(arcsin(x + 1), x, 4)

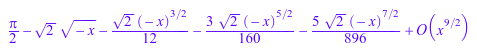
Однако расширение f = ln(x + I*x^3) вокруг точки разветвления 0, который возвращен series не аппроксимирует f для значений x это близко к отрицательной вещественной оси:

f := ln(x + I*x^3);
g := series(f, x, 4);

DIGITS := 20:
float(subs([f, expr(g)], x = -0.01 + 0.0000001*I));
delete DIGITS:

Ситуация подобна для алгебраических точек разветвления:

f := sqrt(x + I*x^3);
g := series(f, x, 4);

DIGITS := 20:
float(subs([f, expr(g)], x = -0.01 + 0.0000001*I));
delete DIGITS:

delete f, g:

Пример 13

Первые шесть сроков, включая обнуляет, следующих двух последовательных расширений согласитесь:

series(sin(tan(x)), x, 12);
series(tan(sin(x)), x, 12);

Если мы хотим вычислить последовательное расширение различия sin(tan(x)) - tan(sin(x)), отмена происходит и производит слишком мало условий в результате. series обнаруживает это автоматически и выполняет второй последовательный расчет с увеличенной точностью:

series(sin(tan(x)) - tan(sin(x)), x, 6)

Это может, тем не менее, произойти, что результат имеет слишком мало условий; cf. Пример 15.

Если рациональные экспоненты происходят в последовательном расширении, то это может даже произойти, что результат имеет больше, чем количество условий, которые требует третий аргумент:

series(x^2*exp(x) + x*sqrt(sin(x)), x, 3)

Пример 14

seriesуправление термина порядка основано на концепции 'относительного порядка', считая количество условий, начинающихся с самого низкоуровневого, которое присутствует в расширении. Управление 'абсолютной командой' может быть достигнуто путем простого добавления соответствующего термина порядка, чтобы ограничить результат, возвращенный series:

series(exp(x) + x*sqrt(sin(x)), x, 7)

series(exp(x) + x*sqrt(sin(x)), x, 7) + O(x^4)

Обратите внимание, однако, что ряд должен иметь достаточно условий для добавленного термина порядка, чтобы оказать любое влияние:

series(exp(x^2), x, 4)

series(exp(x^2), x, 4) + O(x^8)

Пример 15

Если заданный порядок для расширения слишком мал, чтобы вычислить обратную величину (из-за отмены), series отвечает на символьный звонок:

series(exp(x), x, 4)

series(1/(exp(x) - 1 - x - x^2/2 - x^3/6), x, 2)

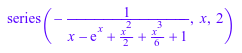
После увеличения порядка расширение вычисляется, но возможно с меньшим количеством условий:

series(1/(exp(x) - 1 - x - x^2/2 - x^3/6), x, 3);
series(1/(exp(x) - 1 - x - x^2/2 - x^3/6), x, 4)

Пример 16

series и int поддержите друг друга. С одной стороны, последовательные расширения могут быть интегрированы:

int(series(1/(2 - x), x), x = 0..1)

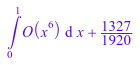
С другой стороны, series знает, как обработать символьные интегралы:

int(x^x, x)

series(%, x = 0, 3)

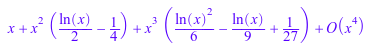
int(exp(-x*sin(t)), t = 0.. x)

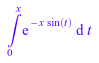
series(%, x = 0)

int(cos((x*t^2 + x^2*t))^(1/3), t = 0..2)

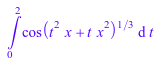
series(%, x)

Пример 17

Пользователи могут расширить степень series путем реализации series атрибуты (пазы) для их собственных специальных математических функций.

Мы иллюстрируем, как записать такой серийный атрибут, с помощью случая показательной функции. (Конечно, эта функция уже имеет series припишите в MuPAD, который можно смотреть через expose(exp::series).) Для того, чтобы не перезаписать уже существующий атрибут, мы работаем над копией показательной функции под названием Exp.

series атрибут должен быть процедурой с четырьмя аргументами. Эта процедура называется каждый раз, когда последовательное расширение Exp с произвольным аргументом должен быть вычислен. Первый аргумент является аргументом Exp в series вызвать. Второй аргумент является серийной переменной; точка расширения всегда является источником 0; другие точки расширения внутренне перемещены до начала координат заменой переменных. Третье и четвертый аргумент идентичны с order и dir аргумент series, соответственно.

Например, команда series(Exp(x^2 + 2), x, 5) внутренне преобразован в вызов Exp::series(x^2 + x, x, 5, Undirected). Вот пример series припишите для Exp.

// The series attribute for Exp. It handles the call
// series(Exp(f), x = 0, order, dir)
ExpSeries := proc(f, x, order, dir)
  local t, x0, s, r, i;
begin
  // Expand the argument into a series.
  t := series(f, x, order, dir);

  // Determine the order k of the lowest term in t, so that
  // t = c*x^k + higher order terms, for some non-zero c.
  k := ldegree(t);

  if k = FAIL then
    // t consists only of an error term O(..)
    return(FAIL);

  elif k < 0 then
    // This corresponds to an expansion of exp around infinity,
    // which does not exist for the exponential
    // function, since it has an essential singularity. Thus we
    // return FAIL, which makes series return unevaluatedly. For
    // other special functions, you may add an asymptotic
    // expansion here.
    return(FAIL);

  else // k >= 0
    // This corresponds to an expansion of exp around a
    // finite point x0. We write t = x0 + y, where all
    // terms in y have positive order, use the
    // formula exp(x0 + y) = exp(x0)*exp(y) and compute
    // the series expansion of exp(y) as the functional
    // composition of the Taylor series of exp(x) around
    // x = 0 with t - x0. If your special function has
    // any finite singularities, then they should be
    // treated here.
    x0 := coeff(t, x, 0);
    s := Series::Puiseux::create(1, 0, order,
           [1/i! $ i = 0..(order - 1)], x, 0, dir);
    return(Series::Puiseux::scalmult(s @ (t - x0), Exp(x0), 0))
  end_if
end_proc:

Эта специальная функция должна быть встроена в функциональную среду. Следующая команда задает Exp как функциональная среда и позволяет системной функции exp сделайте оценку. subs команда, примененная на результат, достигает того Exp с символьными аргументами возвращен как Exp и не как exp.

Exp := funcenv(x -> subs(exp(x), hold(exp)=hold(Exp))):
Exp(1), Exp(-1.0), Exp(x^2 + x)

series может уже обработать эту “новую” функцию, но она может только вычислить Разложение Тейлора с символьными производными:

ORDER := 3: series(Exp(x), x = 0)

Можно задать series атрибут Exp путем присвоения процедуры выше ее series паз:

Exp::series := ExpSeries:

Теперь мы можем протестировать новый атрибут:

series(Exp(x^2 + x), x = 0) = series(exp(x^2 + x), x = 0)

series(Exp(x^2 + x), x = 2) = series(exp(x^2 + x), x = 2)

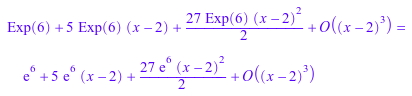
series(Exp(x^2 + x), x = 0, 1)

series(Exp(x^2 + x), x = infinity)

Другая возможность получить последовательные расширения пользовательских функций состоит в том, чтобы задать diff атрибут соответствующей функциональной среды. Это используется series вычислить Разложение Тейлора когда никакой series атрибут существует. Однако это только работает, когда Разложение Тейлора существует, пока series атрибут может обработать более общие типы последовательных расширений также.

delete ExpSeries, Exp:

Возвращаемые значения

Если order неотрицательное целое число, затем series возвращает любого объект доменного типа Series::Puiseux или Series::gseries, выражение типа "series", или, если f RootOf выражение, набор типа Type::Set. Если order = infinity, затем series возвращает арифметическое выражение.

Перегруженный

f