Series::PuiseuxУсеченные последовательные расширения Пюизе
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
Series::Puiseux(f,x, <order>, <dir>) Series::Puiseux(f,x = x0, <order>, <dir>)
Series::Puiseux область для усеченных последовательных расширений. Элементы этой области представляют начальные сегменты Тейлора, Лорана, или последовательных расширений Пюизе, а также немного более общих типов последовательных расширений.
Системная функция series главное приложение этой области. Это пытается вычислить Тейлора, Лорана, или ряд Пюизе или более общее последовательное расширение данного арифметического выражения, и результат возвращен как элемент Series::Puiseux или, возможно, более общего доменного Series::gseries.
Обычно нет никакой потребности в вас явным образом создать элементы этой области. Методы, описанные на этой странице справки, применяются, если вы хотите обработать результат, возвращенный series далее.
Если вы создаете элементы, явным образом аналогичные описанному выше, то какая-либо специальная математическая функция, такая как sin или exp, включение серийной переменной рассматривается как коэффициент. Используйте series расширять такие функции также и использовать конструктора только если f не содержит специальных математических функций. См. Пример 1.
Используйте спецификатор типа Type::Series определить для элемента этой области, какой вид последовательного расширения это.
Функция чувствительна к глобальной переменной ORDER, который определяет количество по умолчанию условий расширения.
Можно создать объекты Series::Puiseux в различных способах. Стандартный метод состоит в том, чтобы использовать конструктора. Второй аргумент задает серийную переменную и точку расширения со значением по умолчанию 0, если не использовано:
Series::Puiseux(x/(1 - x), x); Series::Puiseux(x/(1 - x), x = 2); Series::Puiseux(x/(1 - x), x = complexInfinity);
Третий аргумент, если есть задает желаемое количество условий. Если это не использовано, значение переменной окружения ORDER используется:
Series::Puiseux(x/(1 - x), x = 2, 4); ORDER := 2: Series::Puiseux(x/(1 - x), x); delete ORDER:
Методы const, one, и zero обеспечьте ярлыки для создания последовательных расширений только с постоянным термином или никаким ненулевым термином вообще. Определение порядка остаточного члена обязательно:
Series::Puiseux::const(PI, x, 4); Series::Puiseux::one(x = 2, 3); Series::Puiseux::zero(x = 0, 3/2); Series::Puiseux::zero(x = complexInfinity, 5);
Обратите внимание на то, что, например, O(x^(3/2)) не элемент Series::Puiseux, но может быть преобразован конструктором:
f := O(x^(3/2)); g := Series::Puiseux(f, x); domtype(f), domtype(g)
Оба конструктор Series::Puiseux и метод const расцените специальные математические функции, такие как exp или sin, как коэффициенты:
Series::Puiseux(sin(x)/(1 - x), x, 4); Series::Puiseux::const(cos(x), x = 1, 3);
Используйте системную функцию series если вы хотите расширить специальные функции также:
series(sin(x)/(1 - x), x, 4);
Конструктор возвращает FAIL, если это не может преобразовать вход в элемент Series::Puiseux. Затем series может смочь произвести более общее расширение:
delete a: Series::Puiseux(x^a/(1 - x), x); f := series(x^a/(1 - x), x); domtype(f);
Метод create чисто синтаксический конструктор, где операнды заданы явным образом. Шестые и седьмые аргументы являются дополнительными и по умолчанию к 0 и Undirected, соответственно:
Series::Puiseux::create(3, 1, 5, [1/2, 5], x) = Series::Puiseux::create(3, 1, 5, [1/2, 5], x, 0, Undirected)
Series::Puiseux::create(1, -2, 1, [ln(x), 0, 3], x, complexInfinity);
Мы демонстрируем внутреннюю структуру объектов типа Series::Puiseux:
f := series(exp(x), x = 1); g := series(sin(sqrt(1/x)), x = infinity); h := series(sin(sqrt(-x))/x, x = 0)
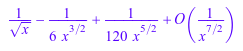
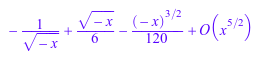
op(f); op(g); op(h)
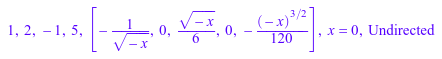
Серия f и g имеют тип 0, в то время как h имеет тип 1:
op(f, 1), op(g, 1), op(h, 1)
Порядок ветвления f 1, и порядок ветвления обоих g и h 2:
op(f, 2), op(g, 2), op(h, 2)
Третье и четвертый операнд определяют порядок ведущего термина и остаточного члена, соответственно:
ldegree(f) = op(f, 3)/op(f, 2), ldegree(g) = op(g, 3)/op(g, 2), ldegree(h) = op(h, 3)/op(h, 2); Series::Puiseux::order(f) = op(f, 4)/op(f, 2), Series::Puiseux::order(g) = op(g, 4)/op(g, 2), Series::Puiseux::order(h) = op(h, 4)/op(h, 2);
Для последовательных расширений типа 0 пятый операнд содержит коэффициенты расширения:
op(f, 5) = [coeff(f)]; op(g, 5) = [coeff(g)];
Однако h расширение типа 1, и затем пятый операнд хранит слагаемых:
op(h, 5); [coeff(h)];
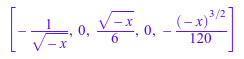
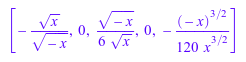
Шестой операнд содержит серийную переменную и точку расширения:
op(f, 6), Series::Puiseux::indet(f), Series::Puiseux::point(f); op(g, 6), Series::Puiseux::indet(g), Series::Puiseux::point(g); op(h, 6), Series::Puiseux::indet(h), Series::Puiseux::point(h);
Расширения f и h являются неориентированными, в то время как g направленное расширение слева вдоль действительной линии к положительной бесконечности:
op(f, 7) = Series::Puiseux::direction(f), op(g, 7) = Series::Puiseux::direction(g), op(h, 7) = Series::Puiseux::direction(h);
Поскольку внутренняя структура может подвергнуться изменениям, получив доступ к операндам и элементу Series::Puiseux через op должен избежаться. Используйте соответствующие методы доступа вместо этого.
Вокруг точек разветвления последовательные расширения типа 1 могут аппроксимировать функцию в более широкой области значений, чем те из типа 0:
f := x -> arcsin(x + 1): g := series(f(x), x, 2); h := series(f(x), x, 2, Right);
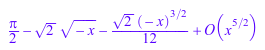
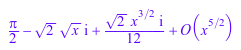
Расширение g, из типа 1, аппроксимирует f хорошо в открытом диске строится в начале координат. Однако расширение h, из типа 0, требовался для положительных действительных значений x только, и на самом деле это не аппроксимирует f на отрицательной вещественной оси и в верхней полуплоскости:
op(g); op(h);
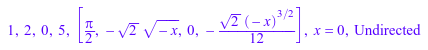
DIGITS := 4: [f(0.01), f(0.01*I), f(-0.01), f(-0.01*I)]; map([g(0.01), g(0.01*I), g(-0.01), g(-0.01*I)], float); map([h(0.01), h(0.01*I), h(-0.01), h(-0.01*I)], float); delete DIGITS:
Метод convert01 преобразует последовательное расширение типа 0 в один из типа 1:
h1 := Series::Puiseux::convert01(h); op(h1);
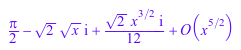
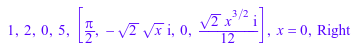
Обратная конверсия, с помощью метода convert10, находится в не всегда возможен:
op(Series::Puiseux::convert10(h1)); op(Series::Puiseux::convert10(g));
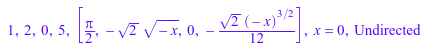
Можно осуществить преобразование при помощи свойств:
assume(x > 0): op(Series::Puiseux::convert10(g)); unassume(x):
Несмотря на имя, элементы Series::Puiseux может содержать коэффициентные функции в зависимости от серийной переменной:
f := series(psi(x), x = infinity, 4); domtype(f), coeff(f, 0)
Относительно дифференцирования, интегрирования и состава, такие расширения ведут себя как функции серийной переменной и не как формальный ряд:
diff(f, x) = series(diff(psi(x), x), x = infinity, 4)
int(f, x) = series(int(psi(x), x), x = infinity, 4)
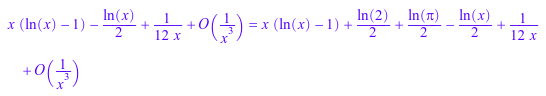
f @ series(2*x, x = infinity) = series(psi(2*x), x = infinity, 4)
Основные арифметические операции реализованы для элементов Series::Puiseux:
f := series(exp(x), x, 4); g := series(sqrt(x)/(1 - x), x, 4); h := series(cot(x), x, 4);
f + g + h; _plus(f, g, h)
f - h = _subtract(f, h); -g = _negate(g);
f*g*h; _mult(f, g, h)
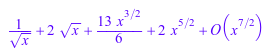
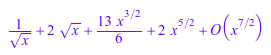
f/g = _divide(f, g); 1/h = _invert(h);
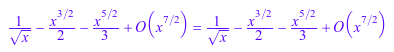
Операнды, которые не имеют типа Series::Puiseux неявно преобразованы в последовательные расширения с той же точкой расширения через конструктора, прежде чем арифметическая операция будет выполнена:
f - 1 - x; h * (sin(x) + x);
Ошибка происходит, когда точки расширения отличаются, или направления расширения несовместимы:
f := series(arccot(x), x = 0, Left); g := series(sqrt(sin(x)), x = 0, Right); f + g
Error: Inconsistent direction. [Series::Puiseux::plus]
h := series(1/x, x = 2, 4); f * h
Error: Both series must use the same variables and expansion points. [Series::Puiseux::mult]
Если направления совместимы, то направление результата указывает минимальный диапазон, где все операнды заданы:
s := series(tanh(x), x, Real);
f + s; Series::Puiseux::direction(%)
Метод scalmult умножение реализаций константой или одним термином:
f := series(1 + 2*x^3, x); Series::Puiseux::scalmult(f, 5) = 5*f; Series::Puiseux::scalmult(f, 5, 3) = 5*x^3*f;
g := series(1 + 2*x^3, x = 2, 3); Series::Puiseux::scalmult(g, 1, 3) = (x - 2)^3*g
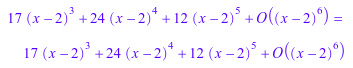
h := series(1 + 2*x^3, x = complexInfinity); Series::Puiseux::scalmult(h, 1, 1/2) = x^(-1/2)*h
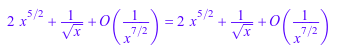
Возведение в степень реализовано для интегральных и рациональных экспонент:
f := series(exp(x), x, 3); f^2 = _power(f, 2); f^(1/3) = _power(f, 1/3)
Экспонентам позволяют быть нерациональными, если последовательное расширение запускается с постоянного слагаемого, независимого от серийной переменной:
f^I = series(exp(I*x), x, 3);
g := series(sin(-x), x); g^I
Error: Exponent must be a rational number. [Series::Puiseux::_power]
Если экспонента содержит серийную переменную, то ошибка происходит:
f^x
Error: Exponent must not contain the series variable. [Series::Puiseux::_power]
Для неориентированных расширений и рациональных экспонент, которые не являются неотъемлемой частью, результат имеет тип 1 в целом:
g^(1/2); op(%, 1);
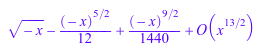
Результат упрощает, когда вы задаете одно из направлений Left или Right:
g := series(sin(-x), x, Left): g^(1/2); op(%, 1);
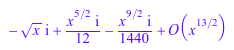
g := series(sin(-x), x, Right): g^(1/2);
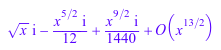
Функциональный состав элементов Series::Puiseux реализован методом _fconcat:
f := series(ln(x), x = 1, 4); g := series(cos(y), y = 0); f@g = _fconcat(f, g); series(ln(cos(y)), y = 0, 4);
Если левый аргумент не имеет типа Series::Puiseux, это неявно расширено вокруг предельной точки правильного аргумента перед составом:
f := series(sin(-x), x = 0); sqrt(y) @ f = Series::Puiseux(sqrt(y), y) @ f;
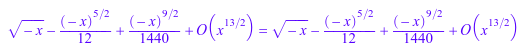
Если правильный аргумент не имеет типа Series::Puiseux, это неявно расширено вокруг источника через конструктора перед составом:
f @ sqrt(y) = f @ Series::Puiseux(sqrt(y), y)
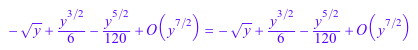
Это не может работать, если аргумент, который будет преобразован, содержит специальные математические функции, но можно явным образом расширить его в ряд через series в этом случае:
f @ tan(y)
f @ series(tan(y), y = 0)
Математически, состав последовательных расширений не задан, если предельная точка правильного аргумента не является точкой расширения левого аргумента:
g := series(y^2 - 1, y = 0); f @ g
f @ (y^2 - 1)
f @ series(y^2 - 1, y = 1, 4)
Метод revert вычисляет инверсию усеченного последовательного расширения относительно состава. Точка расширения инверсии является предельной точкой входа и наоборот:
f := series(ln(x), x = 1, 4); revert(f) = series(exp(x), x = 0, 5)
f := series(cot(x), x = 0); revert(f) = series(arccot(x), x = complexInfinity);
f @ revert(f), revert(f) @ f
Если серийная переменная происходит в коэффициентах, или флаг типа равняется 1, ошибка происходит:
f := series(ln(sin(x)), x); g := series(arcsin(x + 1), x, 2);
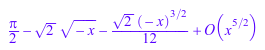
revert(f)
Error: Unable to compute the functional inverse. [Series::Puiseux::revert]
revert(g)
Error: Unable to compute the functional inverse. [Series::Puiseux::revert]
Методы diff и int реализуйте почленное дифференцирование и интегрирование:
f := series(ln(x), x = 1, 4); g := diff(f, x); series(1/x, x = 1, 4); int(g, x);
Если вы указываете диапазон интегрирования, то результатом является арифметическое выражение плюс символьный определенный интеграл O - термин:
int(f, x = 1..2);
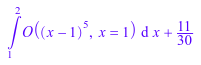
Большинство специальных математических функций перегружается для Series::Puiseux:
f := series(x/(1 - x), x, 4); exp(f) = series(exp(x/(1 - x)), x, 4); ln(f) = series(ln(x/(1 - x)), x, 4);
Если система не может вычислить состав, она возвращает символьный вызов функции с оцененными аргументами:
delete g: g(f)
exp(series(x + 1/x, x = infinity, 5))
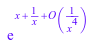
В этом случае можно попробовать series вычислить состав:
series(exp(x + 1/x), x = infinity, 5)
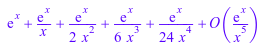
Системные функции Re\Im, и conjugate работайте на все действительные последовательные расширения:
f := series(exp(I*x), x, Real); Re(f) = series(cos(x), x, Real); Im(f) = series(sin(x), x, Real) + O(x^6); conjugate(f) = series(exp(-I*x), x, Real);
Кроме тривиальных случаев, символьный вызов функции возвращен для неориентированного расширения:
Re(series(PI, x)); Re(series(exp(I*x), x));
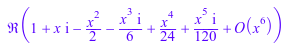
Метод contfrac преобразует последовательное расширение в непрерывную дробь:
f := series(exp(x), x, 10); contfrac(f);
g := series(tan(x), x = PI, 10); contfrac(g);
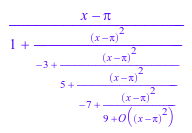
Если коэффициенты последовательного расширения зависят от серийной переменной, то также - коэффициенты соответствующей непрерывной дроби:
h := series(ln(x + 1/x), x = infinity); contfrac(h)
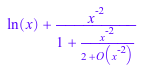
Для последовательных расширений вокруг источника, метод laplace, перегрузка laplace, вычисляет Преобразование Лапласа почленно, если второй аргумент является серийной переменной. Результатом является последовательное расширение вокруг бесконечности:
delete s: f := series(exp(x), x); g := laplace(f, x, s); series(laplace(exp(x), x, s), s = infinity);
Точно так же метод ilaplace вычисляет обратное Преобразование Лапласа почленно для последовательных расширений вокруг бесконечности, если второй аргумент является серийной переменной. Результатом является последовательное расширение приблизительно 0:
ilaplace(g, s, x)
Преобразование Лапласа и обратное Преобразование Лапласа, соответственно, ряда не целесообразны для точек расширения кроме 0 или бесконечность, соответственно, и в этих случаях возвращен символьный вызов функции:
laplace(series(ln(x), x = 1, 2), x, s);
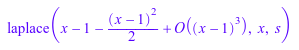
Если второй аргумент не является серийной переменной, то коэффициенты преобразовываются:
h := series(sin(x*y), x = 1, 2); laplace(h, y, s);
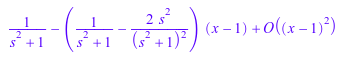
Когда названо одним аргументом, метод coeff возвращает последовательность всех коэффициентов последовательного расширения:
f := series(tan(x), x); coeff(f)
g := series(1/(x - 1)^2, x = infinity); coeff(g)
Когда названо двумя аргументами, coeff возвращает отдельный коэффициент:
coeff(f, -1), coeff(f, 1), coeff(f, 2), coeff(f, 13/2);
Если второй аргумент превышает порядок остаточного члена, coeff возвращает FAIL:
coeff(f, 10)
Когда точкой расширения является complexInfinity, coeff(s, n) возвращает коэффициент
, где x серийная переменная s:
coeff(g, 2), coeff(g, -3), coeff(g, -15/2)
При определении серийной переменной, когда второй или третий аргумент, соответственно, является дополнительным:
coeff(f) = coeff(f, x); coeff(f, 3) = coeff(f, x, 3)
Для последовательных расширений типа 1 “коэффициенты” в целом включают серийную переменную:
h := series(sin(sqrt(-x)), x); coeff(h); coeff(h, 3/2);
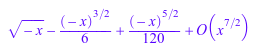
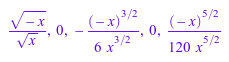
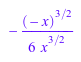
Метод ldegree возвращает порядок ведущего срока последовательного расширения. Когда точкой расширения является complexInfinity и ведущий термин
, затем это - n:
f := series(x*sin(sqrt(-x)), x); g := series(cot(x), x = PI); h := series(2*arccot(x), x = infinity);
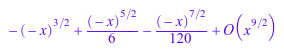
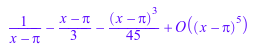
ldegree(f), ldegree(g), ldegree(h)
Метод lcoeff возвращает коэффициент ведущего термина. Для расширения типа 1 это обычно включает серийную переменную:
lcoeff(f), lcoeff(g), lcoeff(h)
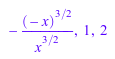
Метод lterm возвращает сам ведущий термин:
lterm(f), lterm(g), lterm(h)
Наконец, метод lmonomial возвращает целое слагаемое:
lmonomial(f) = lcoeff(f)*lterm(f); lmonomial(g) = lcoeff(g)*lterm(g); lmonomial(h) = lcoeff(h)*lterm(h);
Если последовательное расширение состоит только из O - термин, все четыре метода возвращают FAIL:
s := Series::Puiseux::zero(x, 6); ldegree(s), lcoeff(s), lterm(s), lmonomial(s)
Методы nthcoeff, nthmonomial, и nthterm возвратите n th ненулевой коэффициент, одночлен или термин, соответственно, последовательного расширения. В отличие от полиномов, они рассчитывают от термина самых низкоуровневых на, т.е. упорядоченное расположение возрастает экспонентой для конечных точек расширения и убывает экспонентой, когда точкой расширения является complexInfinity:
f := series(x*sin(sqrt(-x)), x); g := series(cot(x), x = PI); h := series(2*arccot(x), x = infinity);
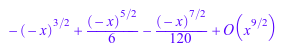
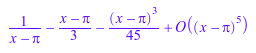
nthcoeff(f, 1) = lcoeff(f); nthmonomial(g, 1) = lmonomial(g); nthterm(h, 1) = lterm(h);
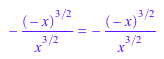
nthcoeff(f, 3), nthmonomial(f, 3), nthterm(f, 3); nthcoeff(g, 3), nthmonomial(g, 3), nthterm(g, 3); nthcoeff(h, 3), nthmonomial(h, 3), nthterm(h, 3);
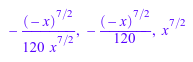
Если второй аргумент не положителен или превышает количество ненулевых слагаемых, все три метода возвращают FAIL:
nthcoeff(f, -4), nthterm(g, 0), nthmonomial(h, 4)
Мы иллюстрируем различие между упорядоченным расположением условий в последовательными расширениями и полиномах. Упорядоченное расположение условий в полиноме согласовывает с упорядоченным расположением условий в последовательном расширении с точкой расширения complexInfinity:
f := poly(2*(x^2 + x)^3); g := series(f, x = complexInfinity); [lcoeff(f), lmonomial(f), lterm(f)]; [lcoeff(g), lmonomial(g), lterm(g)];
[nthcoeff(f, 2), nthmonomial(f, 3), nthterm(f, 4)]; [nthcoeff(g, 2), nthmonomial(g, 3), nthterm(g, 4)];
Для конечных точек расширения, однако, упорядоченное расположение условий в последовательном расширении является реверсом упорядоченного расположения условий в соответствующем полиноме:
h := series(f, x = 0); [lcoeff(h), lmonomial(h), lterm(h)]; [nthcoeff(h, 2), nthmonomial(h, 3), nthterm(h, 4)];
Метод iszero проверки, не имеет ли последовательное расширение никаких ненулевых слагаемых кроме O - термин:
f := series(exp(x), x); g := Series::Puiseux(0, x = 2, 4); iszero(f), iszero(g)
Методы convert попытки преобразовать произвольный объект в элемент Series::Puiseux. Если вход не предлагает точку расширения, convert использование источник:
f := asympt(1/(x + 1), x = infinity); g := sin(x)/(1 - x); h := poly((x + 1)^10); u := O((x - 1)^3, x = 1);
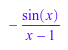
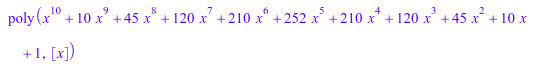
domtype(f), domtype(g), domtype(h), domtype(u)
F := Series::Puiseux::convert(f); G := Series::Puiseux::convert(g); H := Series::Puiseux::convert(h); U := Series::Puiseux::convert(u);
convert возвращает FAIL, если это не может преобразовать вход, например, потому что вход содержит не или больше чем один неопределенный:
Series::Puiseux::convert(sin(1)), Series::Puiseux::convert([1, y, 3])
Метод convert_to попытки преобразовать элемент Series::Puiseux в заданный тип:
Series::Puiseux::convert_to(F, Series::gseries); Series::Puiseux::convert_to(F, contfrac); Series::Puiseux::convert_to(G, DOM_EXPR); Series::Puiseux::convert_to(H, DOM_POLY); Series::Puiseux::convert_to(H, O); Series::Puiseux::convert_to(U, O);
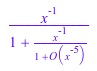
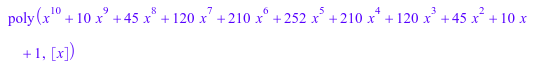
convert_to возвращает FAIL, если это не может выполнить требуемое преобразование:
Series::Puiseux::convert_to(F, O), Series::Puiseux::convert_to(F, DOM_LIST)
Метод expr преобразует элемент Series::Puiseux в арифметическое выражение, отбрасывая O - термин. В общем случае упорядоченное расположение слагаемых не сохраняется:
f := series(exp(x*y), x); g := series(ln(x), x = 1, 3);
expr(f); expr(g);
Метод float применяет системную функцию float ко всем коэффициентам:
float(f); float(g);
Методы combineрасширение, и normal примените соответствующие системные функции ко всем коэффициентам:
delete a, y: f := series(y/(x + y^a), x, 4); g := combine(f); expand(g);
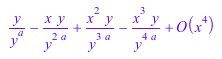
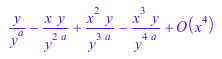
По причинам КПД, арифметическим методам Series::Puiseux обычно не выполняйте символьные упрощения. Используйте expand или normal упростить результаты:
h := series(exp(x), x, 4)^a; expand(h); normal(h);
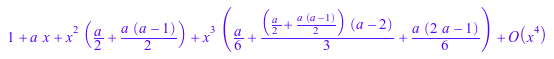
u := series(arctanh(x + y), x, 4); normal(u);
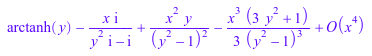
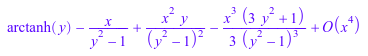
Помимо нормализации коэффициентов, метод normal также удаляет продвижение и конечные нули из списка коэффициентов:
v := Series::Puiseux::create(1, 3, 10,
[0, 1/2, 0, 5, 0, 0], x, 2);
coeff(v);
normal(v);
coeff(%);
Метод map применяет заданную функцию ко всем коэффициентам. Например, системная функция factor не перегружается для Series::Puiseux, но можно использовать map выражать все коэффициенты в учтенной форме:
map(u, factor);
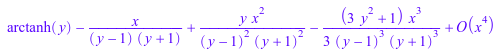
В следующем примере мы используем map умножить все коэффициенты последовательного расширения константой:
w := series(exp(x), x, 3); map(w, _mult, PI) = PI*w
Для последовательных расширений типа 1, map применяет функцию ко всем ненулевым коэффициентам, как возвращено coeff:
z := series(sin(sqrt(-x)), x); coeff(z); map(z, cos);
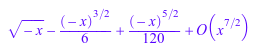
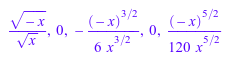
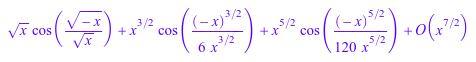
Три различных метода могут использоваться, чтобы заменить серийную переменную: _fconcat, func_call, и subs. Предположим f элемент Series::Puiseux и мы хотим заменить выражением t для серийной переменной x. Затем _fconcat преобразует t в последовательное расширение вокруг источника через конструктора, вычисляет функциональный состав и возвращает результат как элемент Series::Puiseux:
f := series(exp(x), x = 0, 5); Series::Puiseux::_fconcat(f, y) = f @ y; f @ (y^2 + y);
Состав может перестать работать если предельная точка t вокруг источника отличается от точки расширения f или если t содержит специальные математические функции:
f @ (y + 1);
f @ sin(y);
Кроме того, состав не работает если выражение t является постоянным или содержит больше чем один неопределенный:
f @ PI;
Error: Unable to compute composition. [Series::Puiseux::_fconcat]
f @ (x + y);
Error: Unable to compute composition. [Series::Puiseux::_fconcat]
Можно осуществить состав путем явного преобразования t в ряд:
f @ series(y + 1, y = -1); f @ series(sin(y), y = 0); f @ series(x + y, x = -y);
Замена с func_call всегда работает. Это отбрасывает остаточный член, t подставлен буквально, и результатом является выражение и не объект типа Series::Puiseux:
f(5) = Series::Puiseux::func_call(f, 5); f(y) = Series::Puiseux::func_call(f, y);
f(y^2 + y); f(y + 1); f(sin(y)); f(PI); f(x + y);
Наконец, если subs используется, чтобы заменить серийную переменную, только совершенно особые замены позволены (см. описание subs выше для получения дополнительной информации). Затем замена переменной выполняется, и результат снова имеет тип Series::Puiseux:
subs(f, x = y^2 + y)
Error: Invalid substitution. [Series::Puiseux::subs]
subs(f, x = y + 1)
subs(f, x = sin(y))
Error: Invalid substitution. [Series::Puiseux::subs]
subs(f, x = PI)
Error: Invalid substitution. Exactly one indeterminate expected. [Series::Puiseux::subs]
subs(f, x = x + y)
Error: Invalid substitution. Exactly one indeterminate expected. [Series::Puiseux::subs]
Все три метода могут обработать случай, где серийная переменная происходит в коэффициентах:
s := series(ln(x^2 + x), x); s @ (2*y); s(2*y); subs(s, x = 2*y);
Конечно, subs может также использоваться, чтобы заменить другие объекты, чем серийная переменная в коэффициентах и в точке расширения:
g := series(cos(x + y), x, 4); h := series(1/x, x = y, 4);
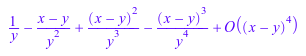
subs(g, y = PI) = series(cos(x + PI), x, 4); subs(h, y = 2) = series(1/x, x = 2, 4);
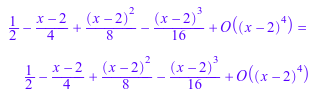
Даже одновременные замены возможны в коэффициентах:
subs(g, [hold(sin) = cos, hold(cos) = sin, y = 2])
Ошибка происходит, если правая сторона содержит серийную переменную:
subs(h, y = x)
Error: Invalid substitution. Right side must not contain the series variable. [Series::Puiseux::subs]
Метод has проверки, происходит ли объект синтаксически в коэффициентах, серийной переменной, точке расширения или направлении элемента Series::Puiseux:
f := series(sin(x + 2*y), x = PI, 2); has(f, x), has(f, y), has(f, PI), has(f, 2), has(f, Undirected); has(f, hold(sin)), has(f, 3), has(f, sin(2*y)), has(f, x - PI);
Последняя возможность возвращает FALSE начиная с выражения x - PI происходит только на экране выход, но не на внутреннем представлении f.
g := series(sign(x), x, Right); has(g, Right), has(g, Undirected);
Метод truncate слагаемые отбрасываний до данного распоряжения:
f := series(x*sin(sqrt(x)), x); Series::Puiseux::truncate(f, 10); Series::Puiseux::truncate(f, 9/2); Series::Puiseux::truncate(f, 7/2); Series::Puiseux::truncate(f, 3); Series::Puiseux::truncate(f, 3/2); Series::Puiseux::truncate(f, 1);
|
Арифметическое выражение, представляющее функцию в |
|
Идентификатор |
|
Точка расширения: арифметическое выражение. Если не заданный, точка 0 расширения по умолчанию используется. |
|
Количество условий, которые будут вычислены: неотрицательное целое число. Распоряжение по умолчанию дано переменной окружения |
|
Любой |
объект доменного типа Series::Puiseux, или значение FAIL, если f не может быть преобразован, например, если степени с нерациональными экспонентами происходят в f.
Вызов элемента Series::Puiseux когда функция отбрасывает остаточный член и заменяет первым аргументом серийную переменную. См. описание метода "func_call" и Пример 22.
Series::Puiseux реализует основную арифметику усеченных последовательных расширений. Используйте обычные арифметические операторы +, -, *, /, ^, и @ для состава.
Арифметические методы Series::Puiseux обычно не выполняйте символьные упрощения. Используйте combineрасширение, или normal запрашивать такие упрощения явным образом.
Смотрите пример 5 и пример 21.
Специальные математические функции, такие как exp или sin, перегружаются для элементов Series::Puiseux; cf. Пример 10.
Системные функции coeff, lcoeff, nthcoeff, ldegree, lmonomial, nthmonomial, lterm, и nthterm работайте над усеченными последовательными расширениями. Обратите внимание на то, что в отличие от полиномов, коэффициенты, одночлены и условия считаются от термина термина самого низкоуровневого на. См. Пример 17.
Используйте функциональный expr преобразовывать последовательное расширение на арифметическое выражение (как элемент области ядра).
Серия доменного типа Series::Puiseux имеет следующие семь операндов:
тип flagt ∈ {0, 1},
ответвление orderb, положительное целое число,
целочисленный v, таким образом, который
порядок ведущего термина,
целочисленный e ≥ v, таким образом, который
порядок остаточного члена,
список коэффициентов l 1, …, l n,
ряд variablex и расширение pointx0 в форме уравнения x = x 0; точкой расширения x 0 может быть complexInfinity также,
направление, Undirectedдействительный, Left, или Right.
Флаг типа различает два различных внутренних представления.
Если t = 0, то операнды выше представляют усеченное последовательное расширение
.
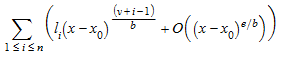Если точкой расширения x 0 является complexInfinity, затем операнды представляют усеченное расширение
.
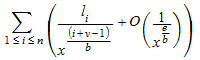Слагаемое
(или
, соответственно) называется одночленом расширения,
степень
(или
, соответственно) называется термином,
l i является соответствующим коэффициентом, и
экспонента
является порядком соответствующего термина или одночлена.
Если t = 1, то операнды выше представляют расширение
.
В этом случае степени x - x 0 явным образом хранится в списке и l, i содержит только условия порядка роста
. Соответствующее расширение для x0 = complexInfinity
,
и l i содержит только условия порядка роста
.
Термин понятий и порядок эквивалентны для t = 0, слагаемое l, i называется одночленом, и соответствующий коэффициент
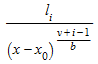
(или
,
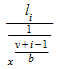соответственно).
Последний тип представления служит для правильных расширений вокруг точек разветвления. Например, если мы хотим расшириться
вокруг x = 0, затем усеченный ряд Пюизе
не аппроксимирует f (x) в более низкой половине комплексной плоскости. С t = 1, расширение
, которое аппроксимирует f (x) также в более низкой части комплексной плоскости около источника, может быть представлено как объект доменного типа Series::Puiseux.
Направление d имеет то же значение как параметр dir из конструктора. Если d = Undirected, операнды выше представляют расширение, допустимое в некотором окружении точки расширения в комплексной плоскости. Обычно, это - открытый диск, сосредоточенный в x0. Если d ≠ Undirected и x 0 представляет вещественное число, это означает, что расширение допустимо для действительных значений x только. Если d = Left или d = Right, то расширение допустимо для x <x 0 или x> x 0, соответственно.
В случае x_0 = complexInfinity, и если d = Undirected, у нас есть расширение, допустимое в окружении Северного полюса Римановой сферы, т.е. для всего
достаточно большого абсолютного значения. Если d = Left, у нас есть расширение вокруг положительной действительной бесконечности, допустимой для достаточно больших действительных значений x. Точно так же, если d = Right, у нас есть расширение вокруг отрицательной действительной бесконечности, допустимой для достаточно больших отрицательных действительных значений x. Наконец, если d = Real, расширение допустимо и вокруг infinity и вокруг - ∞.
См. пример 2.
Как правило, объекты типа Series::Puiseux сгенерированы вызовами series или taylor.