Взаимодействия среды

Эта функция чувствительна к свойствам набора идентификаторов через assume.

Пример 1

Действительная часть 2 e1 ^{+ i}:

Re(2*exp(1 + I))

Пример 2

Re не может извлечь действительную часть символьных выражений, содержащих идентификаторы без значения. Однако в некоторых случаях это может все еще упростить входное выражение, как в следующем двум примерам:

Re(u + v*I)

Re(z + 2*I)

По умолчанию идентификаторы без значения приняты, чтобы представлять произвольные комплексные числа. Можно использовать assume изменить это. Следующая команда говорит систему что z представляет только вещественные числа:

assume(z, Type::Real):
Re(z + 2)

unassume(z)

Пример 3

Если Re не может извлечь действительную часть символьного выражения, попытаться использовать функциональный rectform. Это разделяет сложное выражение z в его действительную и мнимую часть и более мощно, чем Re:

Re(exp(I*sin(z)));
r := rectform(exp(I*sin(z)))

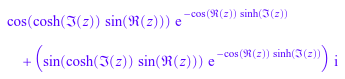
Затем используйте Re(r) извлекать действительную часть r:

Re(r)

Пример 4

Символьные выражения типа "Re" всегда имейте свойство Type::Real, даже если никакой идентификатор символьного выражения не имеет свойство:

is(Re(sin(2*x)), Type::Real)

Пример 5

Можно расширить функции Re и Im к их собственным специальным математическим функциям. Смотрите раздел “Algorithms”. Для этого встройте свою математическую функцию в функцию environmentf и реализуйте поведение функций Re и Im для этой функции как пазы "Re" и "Im" из функциональной среды.

Если подвыражение формы f(u,..) происходит в z, затем Re и Im издайте приказ f::Re(u,..) и f::Im(u,..), соответственно, к стандартной программе паза, чтобы определить действительное и мнимую часть f(u,..), соответственно.

Например, расширьте функциональный Re для синусоидальной функции. Конечно, функциональная среда sin уже имеет "Re" паз. Вызовите свою функциональную среду Sin для того, чтобы не перезаписать существующую системную функцию sin:

Sin := funcenv(Sin):
Sin::Re := proc(u) // compute Re(Sin(u))
  local r, s;
begin
  r := Re(u);
  if r = u then
    return(Sin(u))
  elif not has(r, {hold(Im), hold(Re)}) then
    s := Im(u);
    if not has(s, {hold(Im), hold(Re)}) then
      return(Sin(r)*cosh(s))
    end_if
  end_if;
  return(FAIL)
end:

Re(Sin(2)), Im(Sin(3*I)), Re(Sin(2 + 3*I))

Возвращаемое значение FAIL говорит функциональный Re тот Sin::Re не могло определить действительную часть входного выражения. Результатом является затем символьный Re вызов:

Re(2 + Sin(f(z)))

Возвращаемые значения

арифметическое выражение или контейнерный объект, содержащий такие выражения

Перегруженный

z