Взаимодействия среды

Функция чувствительна к свойствам набора идентификаторов через assume. Смотрите пример 3.

Пример 1

Прямоугольная форма sin (z) для комплексных чисел z:

delete z: r := rectform(sin(z))

Действительное и мнимая часть могут быть извлечены можно следующим образом:

Re(r), Im(r)

Сопряженное комплексное число r может быть получен непосредственно:

conjugate(r)

Пример 2

Действительное и мнимая часть постоянного арифметического выражения могут быть определены функциями Re и Im, как в следующем примере:

Re(ln(-4)) + I*Im(ln(-4))

На самом деле они работают намного быстрее, чем rectform. Однако им не удается вычислить действительное и мнимую часть произвольных символьных выражений, такой что касается термина e ^{i  sin (z)}:

delete z: f := exp(I*sin(z)):
Re(f), Im(f)

Функциональный rectform более мощно. Это может разделить выражение выше в его действительную и мнимую часть:

r := rectform(f)

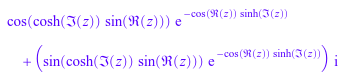
Теперь мы можем извлечь действительное и мнимую часть f:

Re(r)

Im(r)

Пример 3

Идентификаторы без свойств считаются комплексными переменными:

delete z: rectform(ln(z))

Однако можно влиять на поведение rectform путем присоединения свойств к идентификаторам. Например, если z принимает, что только действительные отрицательные величины, действительное и мнимая часть значительно упрощают:

assume(z < 0): rectform(ln(z))

Пример 4

Мы вычисляем прямоугольную форму комплексной переменной x:

delete x: a := rectform(x)

Затем мы делаем то же самое для действительной переменной y:

delete y: assume(y, Type::Real): b := rectform(y)

domtype(a), domtype(b)

Мы сохранили результаты, т.е. элементы доменного типа rectform, в этих двух идентификаторах a и b. Мы вычисляем сумму a и b, который снова имеет доменный тип rectform, т.е. это уже splitted в его действительную и мнимую часть:

c := a + b

domtype(c)

Результат арифметической операции между элементом доменного типа rectform и произвольное арифметическое выражение имеет доменный тип rectform также:

delete z: d := a + 2*b + exp(z)

domtype(d)

Используйте функциональный expr преобразовывать элемент доменного типа rectform в элемент основной области:

expr(d)

domtype(%)

Пример 5

rectform также работает на полиномы и последовательные расширения, а именно, индивидуально на каждом коэффициенте:

delete x, y: p := poly(ln(-4) + y*x, [x]):
rectform(p)

Точно так же rectform работает на списки, наборы или массивы, где это применяется к каждой отдельной записи:

a := array(1..2, [x, y]):
rectform(a)

hfarrays возвращены неизменные:

a := hfarray(1..2, [1.0, 2.0]):
rectform(a)

Обратите внимание на то, что rectform не работает непосредственно на другие типы основных данных. Например, если входное выражение является таблицей арифметических выражений, то rectform отвечает сообщением об ошибке:

a := table("1st" = x, "2nd" = y): 
rectform(a)

Error: Arithmetical expression expected. [rectform::new]

Используйте map применять rectform к операндам такого объекта:

map(a, rectform)

Пример 6

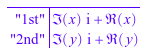
Этот пример иллюстрирует значение трех операндов объекта, возвращенного rectform.

Мы запускаем с выражения x + sin (y), для который rectform может вычислить полное разложение в действительную и мнимую часть:

delete x, y: r := rectform(x + sin(y))

Первые два операнда r действительная и мнимая часть выражения, и третий операнд 0:

op(r)

Затем мы считаем выражение x + f (y), где f (y) представляет неизвестную функцию в комплексной переменной. rectform может разделить x в его действительную и мнимую часть, но не удается сделать это для подвыражения f (y):

delete f: r := rectform(x + f(y))

Первые два операнда возвращенного объекта являются действительным и мнимой частью x, и третий операнд является остатком f (y), для который rectform не смог извлечь любую информацию о ее действительной и мнимой части:

op(r)

Re(r), Im(r)

Иногда rectform не может извлечь любую информацию о действительной и мнимой части входного выражения. Затем третий операнд содержит целое входное выражение, возможно в переписанной форме, из-за рекурсивного режима работы rectform. Первые два операнда 0. Вот пример:

r := rectform(sin(x + f(y)))

op(r)

Re(r), Im(r)

Пример 7

Опытные пользователи могут расширить rectform к их собственным специальным математическим функциям (см. раздел “Backgrounds” ниже). С этой целью встройте свою математическую функцию в функцию environmentf и реализуйте поведение rectform для этой функции как "rectform" паз функциональной среды.

Если подвыражение формы f(u,..) происходит в z, затем rectform издает приказ f::rectform(u,..) к стандартной программе паза, чтобы определить прямоугольную форму f(u,..).

Для рисунка мы показываем, как это работает на синусоидальную функцию. Конечно, функциональная среда sin уже имеет "rectform" паз. Мы вызываем нашу функциональную среду Sin для того, чтобы не перезаписать существующую системную функцию sin:

Sin := funcenv(Sin):
Sin::rectform := proc(u) // compute rectform(Sin(u))
  local r, a, b;
begin
  // recursively compute rectform of u
  r := rectform(u);

   if op(r, 3) <> 0 then
    // we cannot split Sin(u)
    new(rectform, 0, 0, Sin(u))
  else
    a := op(r, 1); // real part of u
    b := op(r, 2); // imaginary part of u
    new(rectform, Sin(a)*cosh(b), cos(a)*sinh(b), 0)
  end_if
end:

delete z: rectform(Sin(z))

Если if условие верно, затем rectform не может разделить u полностью в его действительную и мнимую часть. В этом случае, Sin::rectform не может разделить Sin(u) в его действительную и мнимую часть и указывает на это путем хранения целого выражения Sin(u) в третьем операнде получившегося rectform объект:

delete f: rectform(Sin(f(z)))

op(%)

Возвращаемые значения

Элемент доменного rectform если z арифметическое выражение и объект того же типа как z в противном случае.

Вызовы функции

Вызов элемента rectform когда функция дает к самому объекту, независимо от аргументов. Аргументы не оценены.

Операции

Можно применить (почти) любую функцию к элементам rectform который преобразовывает выражение с комплексным знаком в выражение с комплексным знаком.

Например, можно добавить или умножить те элементы или применить функции, такие как expand и diff им. Результат такой операции, которая не является explicitely, перегруженным методом rectform (см. ниже), элемент rectform.

Эта “автоматическая перегрузка” работает можно следующим образом: Каждый аргумент операции, которая является элементом rectform, преобразован в выражение с помощью метода "expr" (см. ниже). Затем операция применяется, и результат повторно преобразован в элемент rectform.

Используйте функциональный expr преобразовывать элемент rectform к арифметическому выражению (как элемент области ядра).

Функции Re и Im возвратите действительную и мнимую часть элементов rectform.

Операнды

Элемент z rectform состоит из трех операндов: