ViewingBox, ViewingBoxXMin, ViewingBoxXMax, ViewingBoxXRange, ViewingBoxYMin, ViewingBoxYMax, ViewingBoxYRange, ViewingBoxZMin, ViewingBoxZMax, ViewingBoxZRangeВидимая координатная область значений
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
ViewingBox | Обертка библиотеки для “[ViewingBoxXMin .. ViewingBoxXMax, ViewingBoxYMin .. ViewingBoxYMax]” (2D), “[ViewingBoxXMin .. ViewingBoxXMax, ViewingBoxYMin .. ViewingBoxYMax, ViewingBoxZMin .. ViewingBoxZMax]” (3D) | Смотрите ниже |
ViewingBoxXMax, ViewingBoxXMin, ViewingBoxYMax, ViewingBoxYMin, ViewingBoxZMax, ViewingBoxZMin | Дополнительный | Выражение MuPAD® |
ViewingBoxXRange | [ViewingBoxXMin .. ViewingBoxXMax] | Смотрите ниже |
ViewingBoxYRange | [ViewingBoxYMin .. ViewingBoxYMax] | Смотрите ниже |
ViewingBoxZRange | [ViewingBoxZMin .. ViewingBoxZMax] | Смотрите ниже |
| Объекты | Значения по умолчанию |
|---|---|
plot::CoordinateSystem2d |
|
plot::CoordinateSystem3d |
|
ViewingBox атрибуты устанавливают координатную область значений, которая отображается в графике.
ViewingBoxXMin = xmin, ViewingBoxXMax = xmax, эквивалентный ViewingBoxXRange = xmin .. xmax, ограничивает видимость значениями x между xmin и xmax. ViewingBoxYMin и т.д. работайте аналогично.
Установка ViewingBox = [xmin .. xmax, ymin .. ymax] в 2D и ViewingBox = [xmin .. xmax, ymin .. ymax, zmin .. zmax] в 3D
соответственно, служит коротким путем для установки однократных въездов ViewingBoxXMin и т.д.
ViewingBox из графика вычисляется автоматически по умолчанию. Это выбрано в качестве самого маленького поля, содержащего все графические объекты в системе координат.
Значения xmin и т.д. ViewingBox атрибуты должны быть действительными числовыми выражениями или специальным флагом Automatic. С Automatic, система выбирает соответствующие значения автоматически.
Когда графический вывод функции или кривой с сингулярностью, эвристика используется, чтобы установить “разумное” ограниченное поле просмотра для графика. Этому эвристика иногда не удается произвести приятное изображение. Мы рекомендовали запросить явный ViewingBox в таком случае.
При использовании plot::Rotate2d или plot::Rotate3d, ViewingBox может быть больше, чем необходимый. Его размер вычисляется путем вращения общего поля просмотра всех объектов в объекте вращения. Смотрите Пример 4.
ViewingBox из анимации автоматически выбран в качестве объединения всех полей просмотра систем координат анимации.
ViewingBox самостоятельно не может быть анимирован. Однако объект plot::ClippingBox может использоваться, чтобы реализовать анимированные области видимости.
В следующем графике горизонтальная ось помещается в minmal y - значение, произведенное функцией:
f := plot::Function2d(exp(-x^2), x = -1.7 .. 1.7): plot(f)
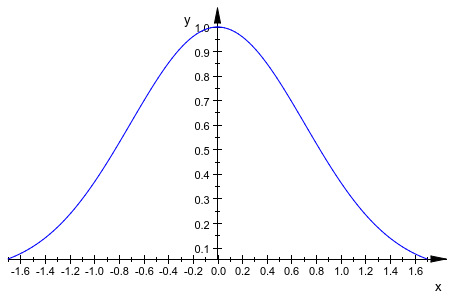
Мы хотим сделать x - ось появляется в y = 0. С этой целью мы запрашиваем область значений y запуститься с y = 0 и использовать Automatic позволять MuPAD найти максимальный y - значение автоматически:
plot(f, ViewingBoxYRange = 0..Automatic)
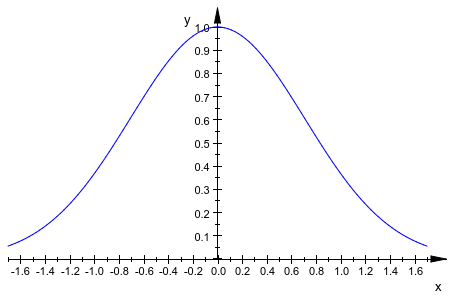
Предыдущая команда эквивалентна:
plot(f, ViewingBoxYMin = 0)
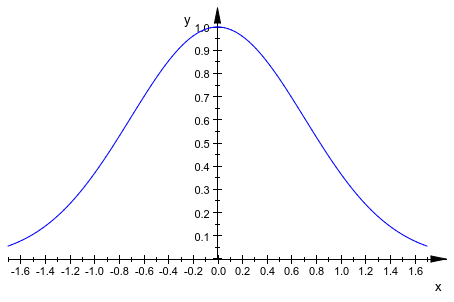
delete f:
Вот 3D график сингулярной функции:
f := plot::Function3d((sin(x) + cos(y))/(x^2 + y^2),
x = -PI..PI, y = -PI..PI):
plot(f)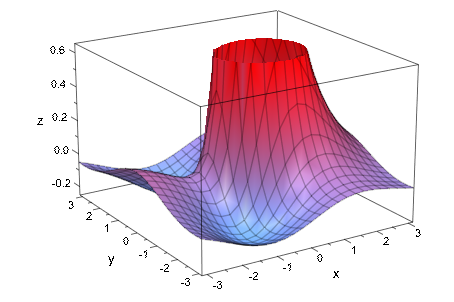
Мы задаем верхнее значение z видимого объема:
plot(f, ViewingBoxZRange = Automatic..3)
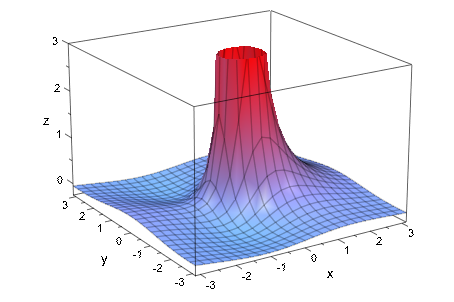
delete f:
Обычно, график использует целый рисунок aera:
f := plot::Function2d(ln(x), x = 0..2): plot(f)
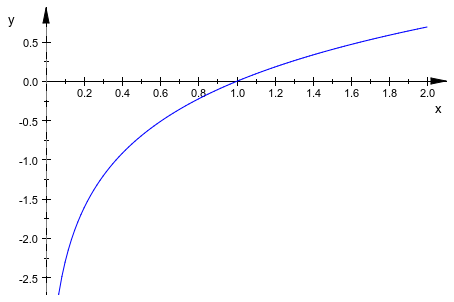
Мы расширяем просмотр, окружают направление x, чтобы сделать его симметричным w.r.t. x:
plot(f, ViewingBoxXRange = -2..2)
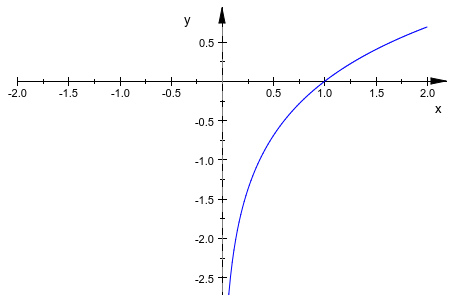
Мы задаем поле просмотра и в x и в направлении y:
plot(f, ViewingBox = [-2..2, -2..2])
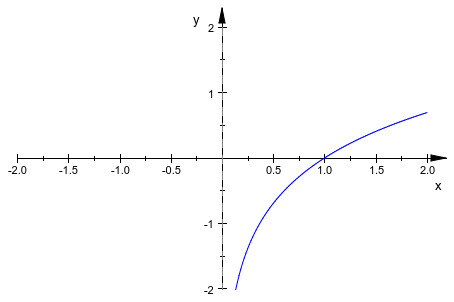
delete f:
Следующее поле просмотра больше, чем ожидалось:
c := plot::Ellipse2d(1, 0.5, [0, 0]): r := plot::Rotate2d(c, PI/3): plot(r)
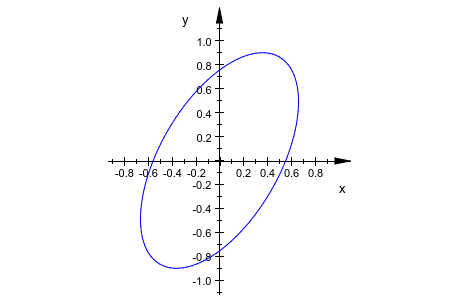
Причина состоит в том, как поле просмотра вращения вычисляется. Синий прямоугольник является полем просмотра эллипса. Вращаемое поле просмотра является черным прямоугольником. Поле просмотра вращения является наименьшим прямоугольником, содержащим вращаемое поле просмотра эллипса (пунктирный черный прямоугольник):
rect1 := plot::Rectangle(-1..1, -0.5..0.5, Color = RGB::Black):
rect2 := plot::modify(rect1, Color = RGB::Blue):
r := plot::Rotate2d(c, rect1, a, a = 0..PI/2):
X := cos(a) + 0.5*sin(a):
Y := 0.5*cos(a) + sin(a):
rect3 := plot::Rectangle(-X..X, -Y..Y, a = 0..PI/2,
Color = RGB::Black,
LineStyle = Dashed):
plot(r, rect2, rect3)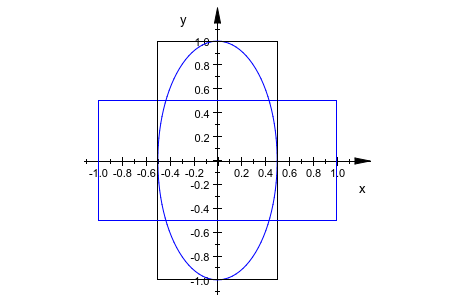
delete c, r, rect1, rect2, rect3, X, Y:
x - располагается от - π к π, сгенерирован всеми системами координат следующей анимации и не изменяется от системы координат до системы координат:
plot(plot::Function2d(sin(x), x = -PI + a .. a, a = 0 .. PI)):