Документация

Вычислите LU-факторизацию

LU-факторизация выражает m ×n матричный A можно следующим образом: P*A = L*U. Здесь L m ×m нижняя треугольная матрица, которая содержит 1 с на основной диагонали, U m ×n матричная верхняя треугольная матрица и P матрица перестановок. Чтобы вычислить LU-разложение матрицы, используйте linalg::factorLU функция. Например, вычислите LU-разложение следующей квадратной матрицы:

A := matrix([[0, 0, 1], [1, 2, 3], [0, 1, 2]]):
[L, U, p] := linalg::factorLU(A)

Вместо того, чтобы возвратить матрицу перестановок P, MuPAD^® возвращает список p с числами, соответствующими строке, обменивается в матричном A. Для n ×n матрица, список p представляет следующую матрицу перестановок с индексами i и j в пределах от 1 к n:

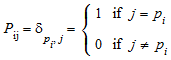Используя это выражение, восстановите матрицу перестановок P из списка p:

P := matrix(3, 3):
for i from 1 to 3 do
   P[i, p[i]] := 1
end_for:
P

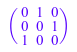
Более эффективно вычислите результат применения матрицы перестановок к A не восстанавливая саму матрицу перестановок:

PA := matrix(3, 3):
for i from 1 to 3 do
  PA[i, 1..3] := A[p[i], 1..3]
end_for:
PA

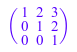
Продукт нижнего треугольного матричного L и верхняя треугольная матрица U исходный матричный A со строками, которыми обмениваются согласно матрице перестановок P:

testeq(PA = L*U)

Теперь вычислите LU-разложение для 3 ×2 матричных B:

B := matrix([[1, 2], [3, 4], [5, 6]]):
[L, U, p] := linalg::factorLU(B)

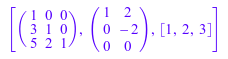
Матрица перестановок для этой LU-факторизации показывает, что порядок строк не изменяется. Поэтому продукт нижнего треугольного матричного L и верхняя треугольная матрица U дает исходный матричный A:

testeq(B = L*U)