Документация

Одномерная линейная регрессия

Регрессия является процессом того, чтобы подбирать модели к данным. Линейная регрессия принимает, что отношение между зависимой переменной y _i и независимой переменной x _i линейно: y _i = a + b  x_i. Здесь a смещение и b наклон линейного соотношения.

Для линейной регрессии выборки данных с одной независимой переменной MuPAD^® обеспечивает stats::linReg функция. Эта функция использует подход наименьших квадратов в вычислении линейной регрессии. stats::linReg выбирает параметры a и b путем минимизации квадратичной ошибки:

Функция также может выполнить линейную регрессию метода взвешенных наименьших квадратов, которая минимизирует

с положительным весом w _i. По умолчанию веса равны 1.

Помимо наклонного a и смещение b из подбиравшей линейной модели, stats::linReg также возвращает значение квадратичного отклонения χ ². Например, подбирайте линейную модель к следующим данным:

x := [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]:
y := [11, 13, 15, 17, 19, 21, 23, 25, 27, 29]:
stats::linReg(x, y)

Линейная модель y _i = 9 + 2 x_i соответствует этим данным отлично. Квадратичная ошибка для этой модели является нулем. Чтобы визуализировать данные и получившуюся модель, отобразите данные на графике при помощи plot::Scatterplot функция. График показывает линии регрессии y _i = 9 + 2 x_i вычисленный stats::linReg:

plot(plot::Scatterplot(x, y))

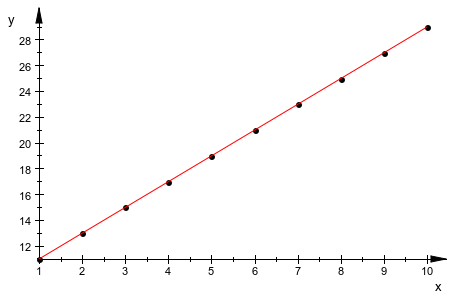
Когда вы работаете с выборками экспериментальных данных, данные почти никогда полностью не подбирают линейной модели. Значение квадратичной ошибки указывает, как далеко фактические данные отклоняются от подобранной модели. Например, измените данные из предыдущего примера путем добавления маленьких случайных значений с плавающей точкой в записи списка y. Затем выполните линейную регрессию для записей списков x и y1 и отобразите данные на графике:

y1 := y + [10*frandom() $ i = 1..10]:
stats::linReg(x, y1);
plot(plot::Scatterplot(x, y1))

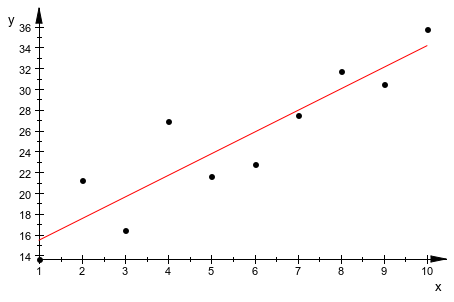
Факт, что stats::linReg находит, что линейная модель, чтобы соответствовать вашим данным не гарантирует, что линейная модель является подходящим вариантом. Например, можно найти, что линейная модель соответствует следующим равномерно распределенным случайным точкам данных:

x := [frandom() $ i = 1..100]:
y := [frandom() $ i = 1..100]:
stats::linReg(x, y);
plot(plot::Scatterplot(x, y))

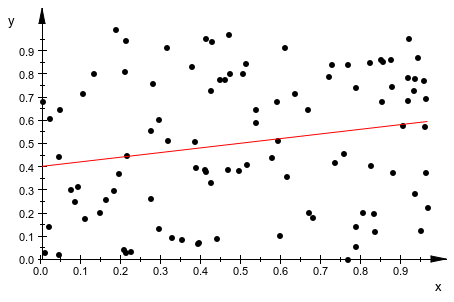
Большое значение квадратичной ошибки указывает, что линейная модель является бедными, в форме для этих данных.

delete x, y, y1