Пример 1

Мы вычисляем средства оценки наименьшего квадрата четырех пар значений, данных в двух списках. Обратите внимание на то, что существует линейное отношение y = 1 + 2 x между записями списков. Минимизированное квадратичное отклонение является 0 указаниями на совершенную подгонку:

stats::linReg([0, 1, 2, 3], [1, 3, 5, 7])

В качестве альтернативы данные могут быть заданы списком пар:

stats::linReg([[1, 1.0], [2, 1.2], [3, 1.3], [4, 1.5]])

Мы принимаем, что переменной y в предыдущем примере является Poissonian, т.е. что измерениям (y _i) = (1.0, 1.2, 1.3, 1.5) дало ошибки стандартное отклонение. Мы обеспечиваем соответствующие веса и оцениваем доверительные интервалы для оценочных функций методом наименьших квадратов при помощи опции CovarianceMatrix:

stats::linReg([[1, 1.0, 1/1.0], [2, 1.2, 1/1.2], 
               [3, 1.3, 1/1.3], [4, 1.5, 1/1.5]], CovarianceMatrix)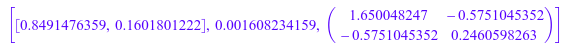

Квадратные корни из диагональных элементов ковариационной матрицы обеспечивают стандартные отклонения для предполагаемых параметров:

sqrt(%[3][1,1]), sqrt(%[3][2,2])

Таким образом мы получаем оценки.

Пример 2

Мы создаем выборку, состоящую из одного столбца строки и двух столбцов нестроки:

stats::sample([["1", 0, 0], ["2", 10, 15], ["3", 20, 30]])

"1"   0   0
"2"  10  15
"3"  20  30

Средства оценки наименьшего квадрата вычисляются с помощью столбцов данных 2 и 3. В этом примере существует только два столбца нестроки, таким образом, индексы столбца не должны быть заданы:

stats::linReg(%)

Пример 3

Мы создаем выборку, состоящую из трех столбцов данных:

stats::sample([[1, 0, 0], [2, 10, 15], [3, 20, 30]])

1   0   0
2  10  15
3  20  30

Мы вычисляем средства оценки наименьшего квадрата для пар данных, данных первым и вторым столбцом:

stats::linReg(%, 1, 2)

Пример 4

Мы создаем выборку трех столбцов, содержащих символьные данные:

stats::sample([[x, y, 0], [2, 4, 15], [3, 20, 30]])

x   y   0
2   4  15
3  20  30

Мы вычисляем символьные средства оценки наименьшего квадрата для пар данных, данных первым и вторым столбцом. Здесь мы задаем эти столбцы списком индексов столбца:

map(stats::linReg(%, [1, 2], CovarianceMatrix), normal)

Пример 5

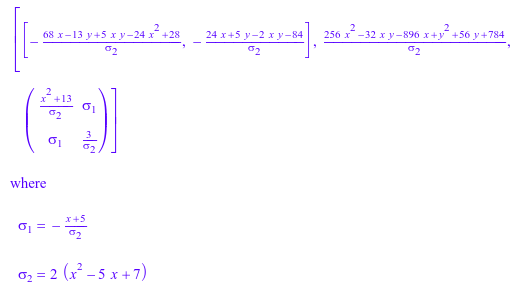
Мы создаем данные (x _i, y _i) с рандомизированным отношением y _i = a + b  x_i:

DIGITS := 5:
r := stats::normalRandom(0, 5):
X := [i $ i = 0..100]:
Y := [12 + 17*x + r() $ x in X]:

Конструкцией отклонения σ (y _i) ² для данных y _i в списке Y равняется 5. Мы используем веса во всех данных:

W := [1/5 $ i = 0..100]:
[ab, chisquared, C]:= stats::linReg(X, Y, W, CovarianceMatrix)

Стандартные отклонения средств оценки a, b является квадратными корнями из диагональных элементов C:

sqrt(float(C[1,1])), sqrt(float(C[2,2]))

Таким образом оценка для a, оценка для b.

delete r, X, Y, W, ab, chisquared, C:

Возвращаемые значения

Без опции CovarianceMatrix, список [[a, b], chisquared] возвращен. Арифметические выражения a и b являются средствами оценки смещение и наклон линейного отношения. Арифметическое выражение chisquared квадратичное отклонение

где a, b является оптимизированными средствами оценки.

С опцией CovarianceMatrix, список [[a, b], chisquared, C] возвращен. Матричный C ковариационная матрица оптимизированных средств оценки a и b.

FAIL возвращен, если средства оценки a и b не существуют.