Geometric camera calibration, также называемый camera resectioning, оценивает параметры линзы и датчика изображения изображения или видеокамеры. Можно использовать эти параметры, чтобы откорректировать для искажения объектива, измерить размер объекта в мировых единицах измерения или определить местоположение камеры в сцене. Эти задачи используются в приложениях, таких как машинное зрение, чтобы обнаружить и измерить объекты. Они также используются в робототехнике для систем навигации и 3-D реконструкции сцены.
Примеры того, что можно сделать после калибровки камеры:

Параметры камеры включают внутренние параметры, значения внешних параметров и коэффициенты искажения. Чтобы оценить параметры камеры, у вас должны быть 3-D мировые точки и их соответствующие 2D точки изображений. Можно получить эти соответствия с помощью повторных изображений калибровочного шаблона, таких как шахматная доска. Используя соответствия, можно решить для параметров камеры. После того, как вы калибруете камеру, чтобы оценить точность предполагаемых параметров, вы можете:
Постройте относительные местоположения камеры и калибровочного шаблона
Вычислите ошибки перепроекции.
Вычислите ошибки оценки параметра.
Используйте Camera Calibrator, чтобы выполнить калибровку фотоаппарата и оценить точность предполагаемых параметров.
Калибровочный алгоритм Computer Vision Toolbox™ использует модель камеры, предложенную Жан-Ивом Буге [3]. Модель включает:
Модель [1] камеры с точечной диафрагмой.
Искажение объектива [2].
Модель камеры с точечной диафрагмой не составляет искажение объектива, потому что идеальная камера с точечной диафрагмой не имеет линзы. Чтобы точно представлять действительную камеру, полная модель камеры, используемая алгоритмом, включает радиальное и тангенциальное искажение объектива.
Камера с точечной диафрагмой является простой камерой без линзы и с одной маленькой апертурой. Световые лучи проходят через апертуру и проецируют перевернутое изображение на противоположной стороне камеры. Думайте о виртуальной плоскости изображения, как являющейся перед камерой и содержащей вертикальное изображение сцены.
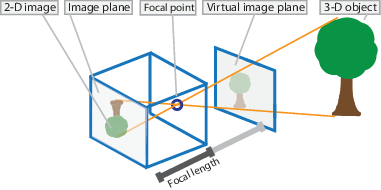
Параметры камеры с точечной диафрагмой представлены в 4 3, матрица вызвала camera matrix. Эта матрица сопоставляет 3-D мировую сцену в плоскость изображения. Калибровочный алгоритм вычисляет матрицу камеры использование внешних и внутренних параметров. Внешние параметры представляют местоположение камеры в 3-D сцене. Внутренние параметры представляют оптическое центральное и фокусное расстояние камеры.
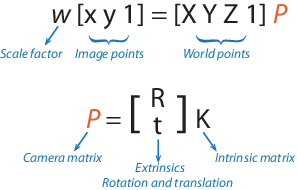
Мировые точки преобразовываются к координатам камеры с помощью параметров значений внешних параметров. Координаты камеры сопоставлены в плоскость изображения с помощью параметров внутренних параметров.
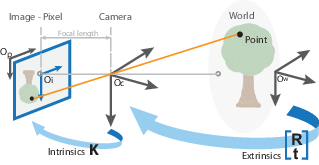
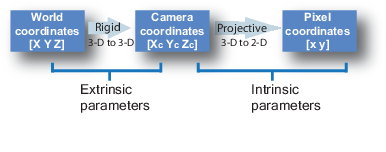
Калибровочный алгоритм вычисляет матрицу камеры использование внешних и внутренних параметров. Внешние параметры представляют твердое преобразование от 3-D системы мировой координаты до системы координат 3-D камеры. Внутренние параметры представляют проективное преобразование от координат 3-D камеры в 2D координаты изображений.
Внешние параметры состоят из вращения, R, и перевода, t. Источник системы координат камеры в ее оптическом центре, и ее x- и ось y- задают плоскость изображения.

Внутренние параметры включают фокусное расстояние, оптический центр, также известный как principal point и скошенный коэффициент. Матрица внутреннего параметра камеры, K, задана как:
Пиксельный скос задан как:
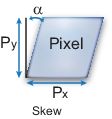
| — Оптический центр (основная точка), в пикселях. |
| — Фокусное расстояние в пикселях. — Фокусное расстояние в мировых единицах измерения, обычно выраженных в миллиметрах. — Размер пикселя в мировых единицах измерения. |
| — Скошенный коэффициент, который является ненулевым, если оси изображений не перпендикулярны. |
Матрица камеры не составляет искажение объектива, потому что идеальная камера с точечной диафрагмой не имеет линзы. Чтобы точно представлять действительную камеру, модель камеры включает радиальное и тангенциальное искажение объектива.
Радиальное искажение происходит, когда световые лучи изгибаются более близкий ребра линзы, чем они делают в ее оптическом центре. Чем меньший линза, тем больше искажение.

Радиальные коэффициенты искажения моделируют этот тип искажения. Искаженные точки обозначаются как (искаженный x, искаженный y):
x, искаженный = x (1 + k 1*r2 + k 2*r4 + k 3*r6)
y, искаженный = y (1 + k 1*r2 + k 2*r4 + k 3*r6)
x, y Неискаженные пиксельные местоположения. x и y находятся в нормированных координатах изображений. Нормированные координаты изображений вычисляются от пиксельных координат путем перевода в оптический центр и деления на фокусное расстояние в пикселях. Таким образом x и y являются безразмерными.
k 1, k 2, и k 3 — Радиальные коэффициенты искажения линзы.
r2 : x 2 + y 2
Как правило, два коэффициента достаточны для калибровки. Для серьезного искажения, такой как в широкоугольных объективах, можно выбрать 3 коэффициента, чтобы включать k 3.
Тангенциальное искажение происходит, когда линза и плоскость изображения не параллельны. Тангенциальные коэффициенты искажения моделируют этот тип искажения.

Искаженные точки обозначаются как (искаженный x, искаженный y):
x, искаженный = x + [2 * p 1 * x * y + p 2 * (r 2 + 2 * x 2)]
y, искаженный = y + [p 1 * (r 2 + 2 *y 2) + 2 * p 2 * x * y]
x, y Неискаженные пиксельные местоположения. x и y находятся в нормированных координатах изображений. Нормированные координаты изображений вычисляются от пиксельных координат путем перевода в оптический центр и деления на фокусное расстояние в пикселях. Таким образом x и y являются безразмерными.
p 1 и p 2 — Тангенциальные коэффициенты искажения линзы.
r2 : x 2 + y 2
[1] Чжан, Z. “Гибкий Новый техник для Калибровки фотоаппарата”. Транзакции IEEE согласно Анализу Шаблона и Искусственному интеллекту. Издание 22, № 11, 2000, стр 1330–1334.
[2] Heikkila, J. и О. Сильвен. “Процедура калибровки фотоаппарата с четырьмя шагами с неявной коррекцией изображений”. Международная конференция IEEE по вопросам распознавания 1997 компьютерного зрения и шаблона.
[3] Bouguet, J. Y. “Тулбокс калибровки фотоаппарата для MATLAB”. Вычислительное видение в Калифорнийском технологическом институте. Тулбокс калибровки фотоаппарата для MATLAB.
[4] Брадский, G. и А. Кэехлер. Изучение OpenCV: компьютерное зрение с библиотекой OpenCV. Севастополь, CA: О'Райли, 2008.