Неустановившиеся системы координат Габора позволяют вам реализовать адаптивный временем или адаптивный частотой анализ сигналов. Функции cqt и icqt используйте неустановившиеся системы координат Габора, чтобы получить постоянное-Q (адаптивное частотой) преобразование (CQT) сигнала. Известная сила неустановившихся систем координат Габора - то, что они включают конструкцию устойчивых инверсий, давая к совершенной реконструкции.
Теория неустановившихся систем координат Габора и эффективные алгоритмы для их реализации происходят из-за Dörfler, Holighaus, Гриля и Velasco [1][2]. Алгоритмы в [1] и [2] реализуют заблокированную фазой версию CQT, который не сохраняет те же фазы, которые были бы получены наивной сверткой. В [3], Schörkhuber, Klapuri, Holighaus и Dörfler разрабатывают эффективные алгоритмы для CQT и обратных CQT, которые действительно подражают коэффициентам, полученным наивной сверткой. Большой Тулбокс Частотно-временного анализа [4] обеспечивает обширный набор алгоритмов для неустановившегося анализа Габора и синтеза.
В стандарте анализ Габора окно фиксированного размера размещает плоскость частоты времени рядом. Неустановившаяся система координат Габора является набором функций работы с окнами различных размеров, которые используются, чтобы разместить плоскость частоты времени рядом. Анализ вейвлета размещает плоскость частоты времени рядом подобным образом. У вас есть гибкость, чтобы изменить плотность выборки вовремя или частоту. Неустановившиеся системы координат Габора полезны в областях, таких как обработка звукового сигнала, где окна частоты времени фиксированного размера не оптимальны. В отличие от кратковременного преобразования Фурье, окна, используемые в постоянном-Q преобразовании, имеют адаптируемую пропускную способность и плотность выборки. В пространстве частоты окна сосредоточены на логарифмически расположенных с интервалами центральных частотах.
Преобразование Фурье f (t) является корреляцией f (t) с ej ω t:
С тех пор ej ω t не имеет компактной поддержки, преобразование Фурье не является идеальным выбором для изучения неустановившихся сигналов. Если содержимое частоты сигнала изменяется в зависимости от времени, преобразование Фурье не получает то, что те изменения или когда те изменения происходят. Раздел плоскости частоты времени, показанной здесь, представляет это поведение преобразования Фурье.
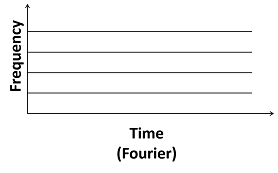
Чтобы выполнить частотно-временной анализ неустановившегося сигнала, запустите с ровной функции работы с окнами с действительным знаком, , который является эффективно ненулевым только на конечном интервале и имеет норму, равную одной. Кроме того, преобразование Фурье сосредоточен в нуле и lowpass. Затем окно f (t) с переводит . Затем возьмите преобразование Фурье результата
Корреляция f (t) с атомами Габора, , стандартный анализ Габора. Путем варьирования u, вы рассматриваете только значения f (t) около времени u. Поддержка определяет размер окружения около времени u. Преобразование Фурье перевод ζ преобразования Фурье и дают
Энергетическая концентрация имеет отклонение σω и сосредоточен в ζ. Если окно, , сдвиги на обычной сетке, преобразовании Фурье продукта переключенного окна и f (t) являются кратковременным преобразованием Фурье (STFT). Мозаичное размещение STFT плоскости частоты времени может быть представлено как сетка полей, каждый сосредоточенный в (u, ζ):
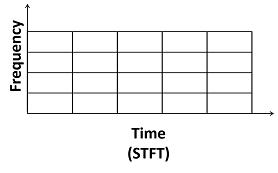
Набор функций известен как систему координат Габора. Элементы этого набора называются атомами Габора. Система координат является набором функций, {hk (t)}, которые удовлетворяют следующему условию: там существуйте константы A> 0, B> 0 таким образом это для любой функции f (t),
Энергетическая концентрация , вовремя, имеет отклонение σt. Энергетическая концентрация , в частоте, имеет отклонение σω. Энергетическая концентрация определяет, как хорошо окно локализует сигнал вовремя и частоту. Принципом неопределенности частоты времени существует предел относительно того, как хорошо можно одновременно локализовать в обоих временных и частотных диапазонах, как обозначено
Сужение окна в одной области приводит к более плохой локализации в другой области. Габор показал, что область окна минимальна когда является Гауссовым.
В CQT варьируются пропускная способность и плотность выборки в частоте. Окна создаются и применяются непосредственно в частотном диапазоне. Различные окна имеют различные центральные частоты и пропускную способность, но отношение центральной частоты к пропускной способности остается постоянным. Поддержание постоянного отношения подразумевает:
Разрешение вовремя улучшается на более высоких частотах.
Разрешение в частоте улучшается на более низких частотах.
Временные сдвиги для каждого окна зависят от пропускной способности, из-за принципа неопределенности.
CQT зависит от:
GK функций окна является четными функциями с действительным знаком. В частотном диапазоне преобразование Фурье GK задано на интервале, [-Fs/2, Фс/2].
Уровень выборки, ζs.
Количество интервалов на октаву, b.
Минимальные и максимальные частоты, ζmin и ζmax.
Выберите минимальную частоту ζmin и количество интервалов на октаву b. Затем сформируйте последовательность из геометрически расположенных с интервалами частот,
ζk = ζmin × 2k/b
для k = 0..., K, где K является целым числом, таким образом, что ζK является самой большой частотой строго меньше, чем частота Найквиста ζs/2. Пропускная способность на kth частоте установлена в Ωk = ζk+1-ζk-1. Учитывая эту выборку, отношение частоты центра kth к пропускной способности окна независимо от k:
Q = ζk/Δk = (21/b-2-1/b)-1.
Чтобы гарантировать совершенную реконструкцию, компонент DC и частота Найквиста предварительно ожидаются и добавляются, соответственно, к последовательности.
W (ω) формирует GK функций окна. W (ω) является с действительным знаком, даже непрерывная функция, которая сосредоточена в 0, положительный в интервале [-½,½], и 0 в другом месте. W (ω) переводится в каждую центральную частоту ζk затем масштабируемый. При оценке масштабированной и переведенной версии W (ω) дает к содействующему GK фильтра [m], данный
GK [m] = W ((m ζs/L - ζk)/Ωk)
для m = 0, …, L-1, где L является длиной сигнала. По умолчанию, cqt использует 'hann' окно.
Принципом неопределенности размер пропускной способности ограничивает значение временных сдвигов. Чтобы удовлетворить неравенству системы координат, сдвиг akof GK должен удовлетворить
ak ≤ ζk/Ωk.
Как упомянуто ранее, окно применяется в частотном диапазоне. Фильтры, GK, сосредоточенный в ζk, сформированы и применены преобразование Фурье сигнала. Взятие обратного преобразования получает постоянные-Q коэффициенты.
[1] Holighaus, N., М. Дерфлер, Г.А. Веласко и Т. Грилл. "Среда для обратимых постоянных-Q преобразований в реальном времени". Транзакции IEEE на Аудио, Речи и Обработке Языка. Издание 21, № 4, 2013, стр 775–785.
[2] Веласко, G. A. Н. Холайос, М. Дерфлер и Т. Грилл. "Создавая обратимое постоянное-Q преобразование с неустановившимися системами координат Габора". В Продолжениях 14-й Международной конференции по вопросам Эффектов Цифрового аудио (DAFx-11). Париж, Франция: 2011.
[3] Schörkhuber, C., А. Клапури, Н. Холайос и М. Дерфлер. "Тулбокс MATLAB для Эффективных Совершенных Преобразований Частоты Времени Реконструкции с Разрешением Логарифмической Частоты". Представленный AES 53-я Международная конференция по вопросам Семантического Аудио. Лондон, Великобритания: 2014.
[4] Průša, Z., П. Л. Сындергэард, Н. Холайос, К. Висмеир и П. Бэлэзс. Большой Тулбокс Частотно-временного анализа 2.0. Звук, Музыка, и Движение, Примечания Лекции в Информатике 2014, стр 419-442. https://github.com/ltfat