Сжатие мультисигнала 1-D с помощью вейвлетов
[XC,DECCMP,THRESH] = mswcmp('cmp',DEC,METH)
[XC,DECCMP,THRESH] = mswcmp('cmp',DEC,METH,PARAM)
[XC,THRESH] = mswcmp('cmpsig',...)
[DECCMP,THRESH] = mswcmp('cmpdec',...)
THRESH = mswcmp('thr',...)
[...] = mswcmp(OPTION,DIRDEC,X,WNAME,LEV,METH)
[...] = mswcmp(OPTION,DIRDEC,X,WNAME,LEV,METH,PARAM)
[...] = mswcmp(...,S_OR_H)
[...] = mswcmp(...,S_OR_H,KEEPAPP)
[...] = mswcmp(...,S_OR_H,KEEPAPP,IDXSIG)
mswcmp вычисляет пороги и, в зависимости от выбранной опции, выполняет сжатие 1D сигналов с помощью вейвлетов.
[XC,DECCMP,THRESH] = mswcmp('cmp',DEC,METH) или
[XC,DECCMP,THRESH] = mswcmp('cmp',DEC,METH,PARAM) возвращает сжатое (обозначенный 'cmp' введите), версия XC из исходного матричного X мультисигнала, чьей структурой разложения вейвлета является DEC. Выход XC получен пороговой обработкой коэффициенты вейвлета: DECCMP, который является разложением вейвлета, сопоставленным с XC (см. mdwtdec), и THRESH матрица пороговых значений. Вход METH имя метода сжатия и PARAM связанный параметр, при необходимости.
Допустимые методы сжатия METH показывают в следующих таблицах. Для методов, которые используют связанный параметр, область значений допустимого PARAM значения также показывают.
'rem_n0' | Удалите близкий 0 |
'bal_sn' | Сбалансируйте норму разреженности |
'sqrtbal_sn' | Сбалансируйте норму разреженности ( |
'scarce' | Недостаточный, |
'scarcehi' | Недостаточный высокий, |
'scarceme' | Недостаточный носитель, |
'scarcelo' | Недостаточный низкий, |
PARAM параметр разреженности, и это должно быть таково что: 1 ≤ PARAM≤ 10 . Для недостаточного метода не сделано никакое управление.
'L2_perf' | Энергетическое отношение |
'N0_perf' | Нулевое содействующее отношение |
PARAM вещественное число, которое представляет необходимую производительность:
0 ≤ PARAM≤ 100 .
'glb_thr' | Глобальный порог |
PARAM действительное положительное число.
'man_thr' | Ручной метод |
PARAM NbSIG- NbLEV матрица или NbSIG- (NbLEV+1) матрицируйте таким образом что:
- PARAM(i,j) порог для коэффициентов детали уровня j для сигнала ith (1 ≤ j ≤ NbLEV).
- PARAM(i,NbLEV+1) порог для коэффициентов приближения для iсигнал th (если KEEPAPP 0).
Где NbSIG количество сигналов и NbLEV количество уровней разложения.
[XC,THRESH] = mswcmp('cmpsig',...) или
[DECCMP,THRESH] = mswcmp('cmpdec',...) или
THRESH = mswcmp('thr',...) Вместо 'cmp' вход OPTION, можно использовать 'cmpsig', 'cmpdec' или 'thr' выбрать другие выходные аргументы. 'thr' возвращает вычисленные пороги, но сжатие не выполняется.
[...] = mswcmp(OPTION,DIRDEC,X,WNAME,LEV,METH) Входной параметр структуры разложения
[...] = mswcmp(OPTION,DIRDEC,X,WNAME,LEV,METH,PARAM) DEC может быть заменен четырьмя аргументами: DIRDECX, WNAME, и LEV. Прежде, чем выполнить сжатие или вычислить пороги, матричный X мультисигнала анализируется на уровне LEV использование вейвлета WNAME, в направлении DIRDEC.
[...] = mswcmp(...,S_OR_H) Могут использоваться еще три дополнительных входных параметров:
[...] = mswcmp(...,S_OR_H,KEEPAPP)
[...] = mswcmp(...,S_OR_H,KEEPAPP,IDXSIG)
S_OR_H ('s' or 'h') обозначает мягкую или трудную пороговую обработку (см. mswthresh для получения дополнительной информации). Значением по умолчанию является 'h'.
KEEPAPP (true or false) указывает, сохранить ли коэффициенты приближения (true) или не (false). Значением по умолчанию является false.
IDXSIG вектор, который содержит индексы начальных сигналов или 'all'. Значением по умолчанию является 'all'.
% Load original 1D-multisignal.
load thinker
% Perform a decomposition at level 2 using wavelet db2.
dec = mdwtdec('r',X,2,'db2');
% Compress the signals to obtain a percentage of zeros
% near 95% for the wavelet coefficients.
[XC,decCMP,THRESH] = mswcmp('cmp',dec,'N0_perf',95);
[Ecmp,PECcmp,PECFScmp] = wdecenergy(decCMP);
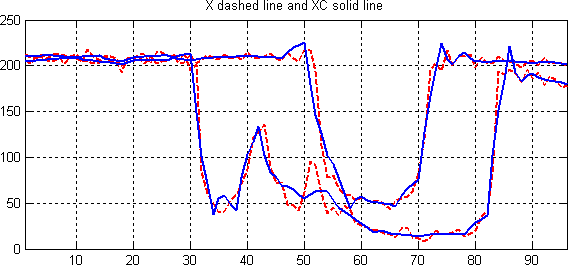
% Plot the original signals 1 and 31, and
% the corresponding compressed signals.
figure;
plot(X([1 31],:)','r--','linewidth',2); hold on
plot(XC([1 31],:)','b','linewidth',2);
grid; set(gca,'Xlim',[1,96])
title('X dashed line and XC solid line')
Бирге Л.; П. Мэссарт (1997), “От Выбора Модели до Адаптивной Оценки”, в Д. Полларде (редактор), Festchrift для Ль. Ле Кама, Спрингера, стр 55–88.
DeVore, Р.А.; Б. Джейрт, Б.Дж. Лукир (1992), “Сжатие изображения Посредством Кодирования Преобразования Вейвлета”, Сделка IEEE на Inf. Теория, издание 38, № 2, стр 719–746.
Donoho, D.L. (1993), “Прогресс Анализа Вейвлета и WVD: Десятиминутный Тур”, происходящий в Анализе Вейвлета и Приложениях, И. Мейере. Роке, стр 109–128. Фронтиерес Эд.
Donoho, Д.Л.; И.М. Джонстон (1994), “Идеальная Пространственная Адаптация Уменьшением Вейвлета”, Biometrika, издание 81, стр 425–455.
Donoho, Д.Л.; И.М. Джонстон, Г. Керкьячариэн, Д. Пикар (1995), “Уменьшение Вейвлета: Asymptopia?” Подмастерье. Рой. Закон Soc., серии B, издание 57 № 2, стр 301–369.
Donoho, Д.Л.; И.М. Джонстон, “Идеальное Шумоподавление в Ортонормированном базисе, Выбранном из Библиотеки Основ”, C.R.A.S. Париж, t. 319, Сер. Я, стр 1317–1322.
Donoho, D.L. (1995), “Шумоподавление Мягкой пороговой обработкой”, Сделка IEEE на Inf. Теория, 41, 3, стр 613–627.