Оцените полиномиальные памятью коэффициенты для цифрового предварительного искажения
Communications Toolbox / Коррекция Нарушений РФ
Оцените полиномиальные памятью коэффициенты для цифрового предварительного искажения (DPD) нелинейного усилителя мощности.
Этот значок показывает блок со всеми включенными портами.
Типы данных |
|
Многомерные сигналы |
|
Сигналы переменного размера |
|
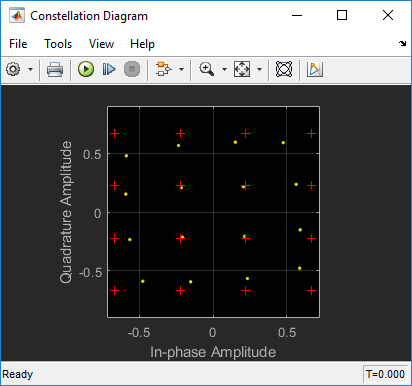
Передачи радиосвязи обычно требуют широкой передачи сигнала пропускной способности по широкому динамическому диапазону сигнала. Чтобы передать сигналы по широкому динамическому диапазону и достигнуть высокой эффективности, усилители ВЧ-мощности (ПЕРВЕНСТВО) обычно действуют в их нелинейной области. Когда эта схема созвездия показывает, нелинейное поведение PA вызывает искажения сигнального созвездия, которые зажимают амплитуду (искажение AM-AM) и скручивают фазу (искажение AM-PM) созвездия указывает пропорциональный амплитуде точки созвездия.
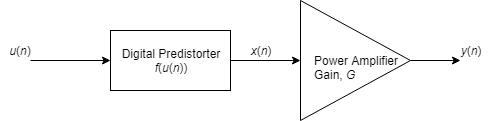
Цель цифрового предварительного искажения состоит в том, чтобы найти нелинейную функцию, которая линеаризует результирующий эффект PA нелинейное поведение в PA выход через рабочий диапазон PA. Когда входом PA является x (n), и функцией перед искажением является f (u (n)), где u (n) является истинным сигналом, который будет усилен, PA, выход приблизительно равен G ×u (n), где G является желаемым амплитудным усилением PA.
Цифровое предыскажение может быть сконфигурировано, чтобы использовать полином памяти с или без перекрестных условий.
Полином памяти с перекрестными условиями предварительно искажает входной сигнал как
Полином памяти с перекрестными условиями имеет (M +M×M× (K-1)) коэффициенты для cm и a mjk.
Полином памяти без перекрестных условий предварительно искажает входной сигнал как
Полином без перекрестных условий имеет M ×K коэффициенты для amk.
Оценка функции перед искажением и коэффициентов
Содействующая оценка DPD использует косвенную архитектуру изучения, чтобы найти, что функциональный f (u (n)) предварительно искажает входной сигнал u (n), который предшествует входу PA.
Содействующие модели алгоритма оценки DPD нелинейные эффекты памяти PA на основе работы в ссылочных статьях Моргана, и др. [1 год], и Schetzen [2], с помощью теоретической основы разрабатываются для систем Волтерры.
А именно, обратное отображение от PA выход, нормированный усилением PA, {y (n)/G}, к входу PA, {x (n)}, предоставляет хорошее приближение функциональному f (u (n)), должен был предварительно исказить {u (n)}, чтобы произвести {x (n)}.
Что касается уравнений полинома памяти выше, оценки вычисляются для полиномиальных памятью коэффициентов:
cm и amjk для полинома памяти с перекрестными условиями
amk для полинома памяти без перекрестных условий
Полиномиальные памятью коэффициенты оцениваются при помощи алгоритма метода наименьших квадратов или рекурсивного алгоритма наименьших квадратов. Алгоритм метода наименьших квадратов или рекурсивные алгоритмы наименьших квадратов использует уравнения полинома памяти выше в полиноме памяти с или без перекрестных условий, заменяя {u (n)} с {y (n)/G}. Функциональный порядок и размерность матрицы коэффициентов заданы степенью и глубиной полинома памяти.
Для примера, который детализирует процесс точной оценки полиномиальных памятью коэффициентов и предварительного искажения входного сигнала PA, смотрите Характеристику Усилителя мощности с DPD для Уменьшаемого Искажения Сигнала.
Для фонового материала ссылки смотрите работы, перечисленные в [1] и [2].
[1] Морган, Деннис Р., Чжэнсян Ма, Джэехиеонг Ким, Михаэль Г. Цирдт и Джон Пэсталан. "Обобщенная Модель Полинома Памяти для Цифрового Предварительного искажения Усилителей мощности". IEEE® Transactions на Обработке сигналов. Издание 54, Номер 10, октябрь 2006, стр 3852–3860.
[2] М. Шецен. Волтерра и винеровские теории нелинейных систем. Нью-Йорк: Вайли, 1980.
