Этот пример показывает вам, как спроектировать контроллер сервомотора для следующей системы.
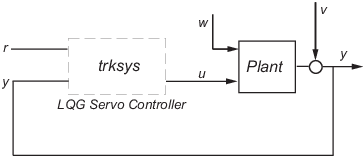
Объект имеет три состояния (x), два входных параметров управления (u), два случайных входных параметров (w), один выход (y), шум измерения для выхода (v), и следующее состояние и уравнения измерения:
где
Система имеет следующие шумовые данные о ковариации:
Используйте следующую функцию стоимости, чтобы задать компромисс между производительностью средства отслеживания и усилием по управлению:
Спроектировать контроллер сервомотора LQG для этой системы:
Создайте систему пространства состояний путем ввода следующего в Окне Команды MATLAB:
A = [0 1 0;0 0 1;1 0 0]; B = [0.3 1;0 1;-0.3 0.9]; G = [-0.7 1.12; -1.17 1; .14 1.5]; C = [1.9 1.3 1]; D = [0.53 -0.61]; H = [-1.2 -0.89]; sys = ss(A,[B G],C,[D H]);
Создайте оптимальное усиление обратной связи состояния с помощью данной функции стоимости путем ввода следующих команд:
nx = 3; %Number of states ny = 1; %Number of outputs Q = blkdiag(0.1*eye(nx),eye(ny)); R = [1 0;0 2]; K = lqi(ss(A,B,C,D),Q,R);
Создайте средство оценки состояния Кальмана с помощью данных шумовых данных о ковариации путем ввода следующих команд:
Qn = [4 2;2 1]; Rn = 0.7; kest = kalman(sys,Qn,Rn);
Соедините средство оценки состояния Кальмана и оптимальное усиление обратной связи состояния, чтобы сформировать контроллер сервомотора LQG путем ввода следующей команды:
trksys = lqgtrack(kest,K)
>> trksys = lqgtrack(kest,K)
a =
x1_e x2_e x3_e xi1
x1_e -2.373 -1.062 -1.649 0.772
x2_e -3.443 -2.876 -1.335 0.6351
x3_e -1.963 -2.483 -2.043 0.4049
xi1 0 0 0 0
b =
r1 y1
x1_e 0 0.2849
x2_e 0 0.7727
x3_e 0 0.7058
xi1 1 -1
c =
x1_e x2_e x3_e xi1
u1 -0.5388 -0.4173 -0.2481 0.5578
u2 -1.492 -1.388 -1.131 0.5869
d =
r1 y1
u1 0 0
u2 0 0
Input groups:
Name Channels
Setpoint 1
Measurement 2
Output groups:
Name Channels
Controls 1,2
Continuous-time model.