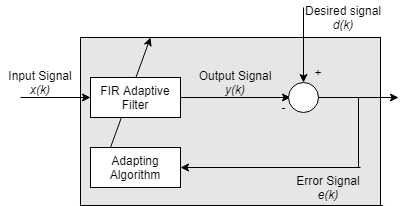
Адаптивные фильтры являются цифровыми фильтрами чье содействующее изменение с целью заставить фильтр сходиться к оптимальному состоянию. Критерий оптимизации является функцией стоимости, которая является обычно средним квадратичным сигнала ошибки между выходом адаптивного фильтра и желаемым сигналом. Когда фильтр адаптирует свои коэффициенты, среднеквадратичная погрешность (MSE) сходится к своему минимальному значению. В этом состоянии адаптируется фильтр, и коэффициенты сходились к решению. Фильтр вывел, y(k), как затем говорят, соответствует очень тесно к желаемому сигналу, d(k). Когда вы изменяете характеристики входных данных, иногда названные средой фильтра, фильтр адаптируется к новой среде путем генерации нового набора коэффициентов для новых данных.
Общий адаптивный алгоритм фильтра
Адаптивный объект фильтра | Адаптация алгоритма |
|---|---|
Блокируйте КИХ LMS адаптивный алгоритм фильтра | |
Фильтрованный-x КИХ LMS адаптивный алгоритм фильтра | |
КИХ LMS адаптивный алгоритм фильтра Нормированный КИХ LMS адаптивный алгоритм фильтра КИХ Sign-data LMS адаптивный алгоритм фильтра КИХ Sign-error LMS адаптивный алгоритм фильтра КИХ Sign-sign LMS адаптивный алгоритм фильтра |
Адаптивный блок фильтра | Адаптация алгоритма |
|---|---|
Блокируйте КИХ LMS адаптивный алгоритм фильтра | |
Блокируйте КИХ LMS адаптивный алгоритм фильтра в частотном диапазоне | |
КИХ LMS адаптивный алгоритм фильтра Нормированный КИХ LMS адаптивный алгоритм фильтра КИХ Sign-data LMS адаптивный алгоритм фильтра КИХ Sign-error LMS адаптивный алгоритм фильтра КИХ Sign-sign LMS адаптивный алгоритм фильтра | |
| LMS Update | КИХ-вес LMS обновляет алгоритм Нормированный КИХ-вес LMS обновляет алгоритм КИХ-вес Sign-data LMS обновляет алгоритм КИХ-вес Sign-error LMS обновляет алгоритм КИХ-вес Sign-sign LMS обновляет алгоритм |
Адаптивный объект фильтра | Адаптация алгоритма |
|---|---|
Быстро трансверсальный алгоритм адаптации наименьших квадратов Раздвижное окно алгоритм адаптации FTF | |
Алгоритм адаптации QR-decomposition RLS Домовладелец алгоритм адаптации RLS Домовладелец алгоритм адаптации SWRLS Алгоритм адаптации рекурсивных наименьших квадратов (RLS) Раздвижное окно (SW) алгоритм адаптации RLS |
Адаптивный блок фильтра | Адаптация алгоритма |
|---|---|
Экспоненциально взвешенный алгоритм рекурсивных наименьших квадратов (RLS) |
Адаптивный объект фильтра | Адаптация алгоритма |
|---|---|
Аффинный алгоритм проекции, который использует прямую матричную инверсию Аффинный алгоритм проекции, который использует рекурсивное матричное обновление Блокируйте аффинный алгоритм адаптации проекции |
Адаптивный объект фильтра | Адаптация алгоритма |
|---|---|
Ограниченный алгоритм адаптации частотного диапазона Неограниченный алгоритм адаптации частотного диапазона Разделенный и ограниченный алгоритм адаптации частотного диапазона Разделенный и неограниченный алгоритм адаптации частотного диапазона |
Адаптивный блок фильтра | Адаптация алгоритма |
|---|---|
Ограниченный алгоритм адаптации частотного диапазона Неограниченный алгоритм адаптации частотного диапазона Разделенный и ограниченный алгоритм адаптации частотного диапазона Разделенный и неограниченный алгоритм адаптации частотного диапазона |
Адаптивный объект фильтра | Адаптация алгоритма |
|---|---|
Градиент адаптивный алгоритм адаптации фильтра решетки Наименьшие квадраты образовывают решетку алгоритм адаптации Разложение QR алгоритм адаптации RLS |
Для получения дополнительной информации об этих алгоритмах обратитесь к разделу алгоритма соответствующих страниц с описанием. Полные описания теории появляются в адаптивных ссылках фильтра [1] и [2].
В устойчивом состоянии, когда фильтр адаптировался, ошибка между фильтром, выход и желаемый сигнал минимальны, не нуль. Эта ошибка известна как установившуюся ошибку. Скорость, с которой фильтр сходится к оптимальному состоянию, известному как быстроту сходимости, зависит от нескольких факторов такая природа входного сигнала, выбор адаптивного алгоритма фильтра и размер шага алгоритма. Выбор алгоритма фильтра обычно зависит факторы, такие как производительность сходимости, требуемая для приложения, вычислительной сложности алгоритма, устойчивости фильтра в среде и любых других ограничений.
LMS-алгоритм прост реализовать, но имеет проблемы устойчивости. Нормированная версия LMS-алгоритма идет с улучшенной быстротой сходимости, большей устойчивостью, но увеличила вычислительную сложность. Для примера, который сравнивает эти два, смотрите, Сравнивают Производительность Сходимости Между LMS-алгоритмом и Нормированным LMS-алгоритмом. Алгоритмы RLS очень устойчивы, сделайте очень хорошо в изменяющихся во времени средах, но являются в вычислительном отношении более комплексными, чем LMS-алгоритмы. Для сравнения смотрите, Сравнивают RLS и Адаптивные Алгоритмы Фильтра LMS. Аффинные фильтры проекции преуспевают, когда вход окрашен, и имейте очень хорошую производительность сходимости. Адаптивные фильтры решетки обеспечивают хорошую сходимость, но идут с увеличенной вычислительной стоимостью. Выбор алгоритма зависит от среды и специфических особенностей приложения.
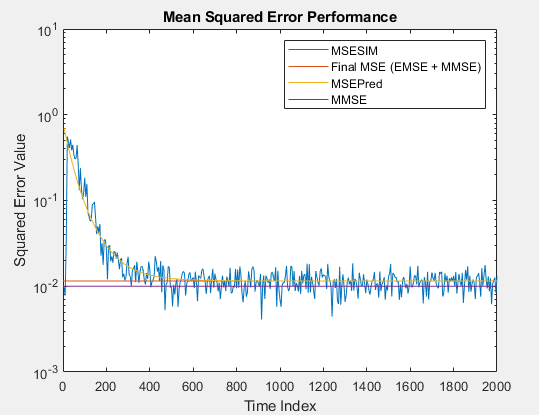
Минимизация среднего квадратичного сигнала ошибки между выходом адаптивного фильтра и желаемым сигналом является наиболее распространенным критерием оптимизации адаптивных фильтров. Фактический MSE (MSESIM) адаптивного фильтра, который вы реализуете, может быть определен с помощью msesim функция. Траектория этого MSE, как ожидают, будет следовать за тем из предсказанных MSE (MSEPred), который вычисляется с помощью msepred функция. Минимальная среднеквадратичная погрешность (MMSE) оценивается msepred функция с помощью Винеровского фильтра. Фильтр Вайнера минимизирует среднеквадратическую ошибку между желаемым сигналом и входным сигналом, отфильтрованным Винеровским фильтром. Большое значение среднеквадратической ошибки указывает, что адаптивный фильтр не может точно отследить желаемый сигнал. Минимальное значение среднеквадратической ошибки гарантирует, что адаптивный фильтр оптимален. Избыточная среднеквадратичная погрешность (EMSE), определенная msepred функционируйте, различие между MSE, введенным адаптивными фильтрами и MMSE, произведенным соответствующим Винеровским фильтром. Итоговый MSE, показанный ниже, является суммой EMSE и MMSE, и равняется предсказанному MSE после сходимости.
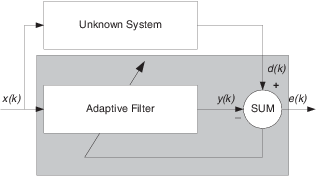
Одно общее адаптивное приложение фильтра должно использовать адаптивные фильтры, чтобы идентифицировать неизвестную систему, такую как ответ неизвестного коммуникационного канала или частотная характеристика аудитории, выбрать довольно расходящиеся приложения. Другие приложения включают отмену эха и идентификацию канала.
В фигуре неизвестная система помещается параллельно с адаптивным фильтром. Это размещение представляет только одну из многих возможных структур. Заштрихованная область содержит адаптивную систему фильтра.
Безусловно, когда e (k) очень мал, адаптивный ответ фильтра близко к ответу неизвестной системы. В этом случае тот же вход питает и адаптивный фильтр и неизвестное. Если, например, неизвестная система является модемом, вход часто представляет белый шум и является частью звука, вы получаете известие от своего модема, когда вы входите в систему своего поставщика интернет-услуг.
Путем размещения неизвестной системы последовательно с адаптивным фильтром фильтр адаптируется, чтобы стать инверсией неизвестной системы, когда e (k) становится очень маленьким. Как показано в фигуре, процесс требует, чтобы задержка, вставленная в желаемый путь к сигналу d (k), сохранила данные при суммировании синхронизируемыми. Добавление задержки сохраняет систему причинной.
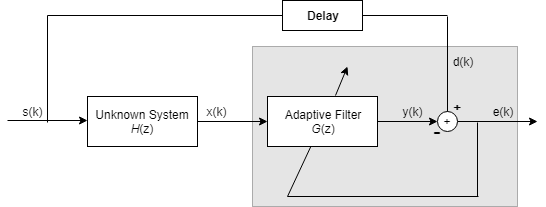
Включая задержку, чтобы составлять задержку, вызванную неизвестной системой, предотвращает это условие.
Простые телефонные сети (POTS) обычно используют обратную систему идентификации, чтобы компенсировать медный носитель передачи. Когда вы отправляете данные или речь по телефонным линиям, медные провода ведут себя как фильтр, имея ответ, который прокручивается прочь на более высоких частотах (или скорости передачи данных) и наличие других аномалий также.
Добавление адаптивного фильтра, который имеет ответ, который является инверсией проводного ответа и конфигурирования фильтра, чтобы адаптироваться в режиме реального времени, позволяет фильтру компенсировать спад и аномалии, увеличивая доступную область значений частотного вывода и скорость передачи данных для телефонной сети.
В подавлении помех адаптивные фильтры позволяют вам удалить шум из сигнала в режиме реального времени. Здесь, желаемый сигнал, тот, чтобы вымыться, комбинирует шум и желаемую информацию. Чтобы удалить шум, накормите сигналом n' (k) адаптивный фильтр, который коррелируется к шуму, который будет удален из желаемого сигнала.
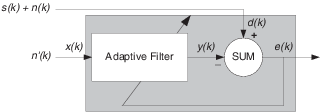
Пока входной шум к фильтру остается коррелированым к нежелательному шуму, сопровождающему желаемый сигнал, адаптивный фильтр настраивает свои коэффициенты, чтобы уменьшать значение различия между y (k) и d (k), удаляя шум и приводя к чистому сигналу в e (k). Заметьте, что в этом приложении, сигнал ошибки на самом деле сходится к сигналу входных данных, вместо того, чтобы сходиться, чтобы обнулить.
Предсказание сигналов требует, чтобы вы сделали некоторые ключевые предположения. Примите, что сигнал является или устойчивым или медленно различным в зависимости от времени и периодическим в зависимости от времени также.
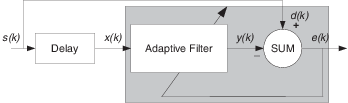
Принимая эти предположения, адаптивный фильтр должен предсказать будущие значения желаемого сигнала на основе прошлых значений. Когда s (k) является периодическим, и фильтр достаточно длинен, чтобы помнить, что предыдущие значения, эта структура с задержкой входного сигнала, могут выполнить предсказание. Вы можете использовать эту структуру, чтобы удалить периодический сигнал из стохастических шумовых сигналов.
Наконец, заметьте, что большинство систем интереса содержит элементы больше чем одной из четырех адаптивных структур фильтра. Тщательно рассмотрение действительной структуры может потребоваться, чтобы определять то, к чему адаптируется адаптивный фильтр.
Кроме того, для ясности в фигурах не появляются аналого-цифровое (A/D) и цифро-аналоговые компоненты (D/A). Поскольку адаптивные фильтры приняты, чтобы быть цифровыми по своей природе, и многие проблемы производят аналоговые данные, преобразование входных сигналов к и от аналоговой области, вероятно, необходимо.
[1] Hayes, Монсон Х., Статистическая Цифровая обработка сигналов и Моделирование. Хобокен, NJ: John Wiley & Sons, 1996, pp.493–552.
[2] Haykin, Саймон, адаптивная теория фильтра. Верхний Сэддл-Ривер, NJ: Prentice-Hall, Inc., 1996.