iradon функционируйте инвертирует Радон, преобразовывают и может поэтому использоваться, чтобы восстановить изображения.
Как описано в Преобразовании Радона, учитывая изображение I и набор углов theta, radon функция может использоваться, чтобы вычислить, Радон преобразовывают.
R = radon(I,theta);
Функциональный iradon может затем быть назван, чтобы восстановить изображение I из данных о проекции.
IR = iradon(R,theta);
В примере выше, проекции вычисляются от оригинального изображения I.
Обратите внимание, однако, что в большинстве областей применения, нет никакого оригинального изображения, из которого формируются проекции. Например, обратный Радон преобразовывают, обычно используется в приложениях томографии. В томографии поглощения рентгена проекции формируются путем измерения затухания излучения, которое проходит через физический экземпляр под различными углами. Оригинальное изображение может считаться сечением через экземпляр, в котором значения интенсивности представляют плотность экземпляра. Проекции собраны с помощью оборудования особого назначения, и затем внутреннее изображение экземпляра восстановлено iradon. Это допускает неразрушающую обработку изображений внутренней части живого организма или другого непрозрачного объекта.
iradon восстанавливает изображение от проекций параллельного луча. В геометрии параллельного луча каждая проекция формируется путем объединения набора линейных интегралов через изображение под определенным углом.
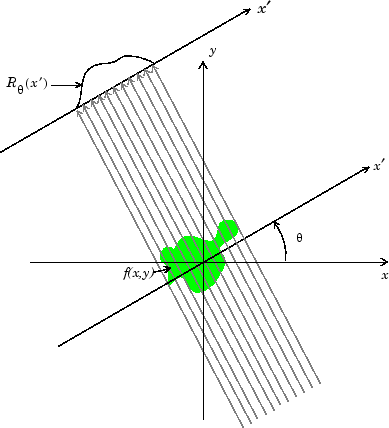
Следующая фигура иллюстрирует, как геометрия параллельного луча применяется в томографии поглощения рентгена. Обратите внимание на то, что существует равное количество n-эмиттеров и n датчиков. Каждый датчик измеряет излучение, испускаемое от его соответствующего эмиттера, и затухание в излучении дает меру интегрированной плотности или массу, объекта. Это соответствует линейному интегралу, который вычисляется в Радоне, преобразовывают.
Геометрия параллельного луча, используемая в фигуре, совпадает с геометрией, которая была описана в Преобразовании Радона. f(x,y) обозначает яркость изображения и проекция в угловой тете.
Проекции параллельного луча через объект
Другая геометрия, которая обычно используется, является геометрией луча вентилятора, в которой существует один источник и n датчики. Для получения дополнительной информации смотрите Проекцию Луча Вентилятора. Чтобы преобразовать данные о проекции параллельного луча в данные о проекции луча вентилятора, используйте para2fan функция.
iradon использование отфильтрованный алгоритм задней проекции, чтобы вычислить обратный Радон преобразовывает. Этот алгоритм формирует приближение изображения I на основе проекций в столбцах R. Более точный результат может быть получен при помощи большего количества проекций в реконструкции. Как количество проекций (длина theta) увеличения, восстановленное изображение IR более точно аппроксимирует оригинальное изображение I. Векторный theta должен содержать монотонно увеличивающие угловые значения с постоянным инкрементным углом Dtheta. Когда скалярный Dtheta известен, это может быть передано iradon вместо массива значений теты. Вот пример.
IR = iradon(R,Dtheta);
Отфильтрованный алгоритм задней проекции фильтрует проекции в R и затем восстанавливает изображение с помощью отфильтрованных проекций. В некоторых случаях шум может присутствовать в проекциях. Чтобы удалить высокочастотный шум, примените окно к фильтру, чтобы ослабить шум. Много таких оконных фильтров доступны в iradon. Вызов в качестве примера iradon ниже применяет Окно Хэмминга к фильтру. Смотрите iradon страница с описанием для получения дополнительной информации. Чтобы получить неотфильтрованные данные о задней проекции, задайте 'none' для параметра фильтра.
IR = iradon(R,theta,'Hamming');
iradon также позволяет вам задать нормированную частоту, D, выше которого фильтр имеет нулевой ответ. D должен быть скаляр в области значений [0,1]. При использовании этой опции перемасштабируется ось частоты так, чтобы целый фильтр был сжат, чтобы поместиться в частотный диапазон [0,D]. Это может быть полезно в случаях, где проекции содержат мало высокочастотной информации, но существует высокочастотный шум. В этом случае шум может быть полностью подавлен, не ставя под угрозу реконструкцию. Следующий вызов iradon устанавливает нормированное значение частоты 0,85.
IR = iradon(R,theta,0.85);
Команды ниже иллюстрируют, как восстановить изображение из параллельных данных о проекции. Тестовое изображение является фантомом главы Shepp-Логана, который может быть сгенерирован с помощью phantom функция. Фантомное изображение иллюстрирует многие качества, которые найдены в реальной томографической обработке изображений человеческих голов. Яркий эллиптический интерпретатор вдоль внешнего вида походит на череп, и много замещающих знаков внутри походят на мозговые функции.
Создайте главное фантомное изображение Shepp-Логана.
P = phantom(256); imshow(P)

Вычислите преобразование Радона фантомного мозга для трех различных наборов значений теты. R1 имеет 18 проекций, R2 имеет 36 проекций и R3 имеет 90 проекций.
theta1 = 0:10:170; [R1,xp] = radon(P,theta1); theta2 = 0:5:175; [R2,xp] = radon(P,theta2); theta3 = 0:2:178; [R3,xp] = radon(P,theta3);
Отобразитесь график одного из преобразований Радона Shepp-Логана возглавляют фантом. Следующий рисунок показывает R3, преобразование с 90 проекциями.
figure, imagesc(theta3,xp,R3); colormap(hot); colorbar
xlabel('\theta'); ylabel('x\prime');Преобразование радона главного фантома Используя 90 проекций
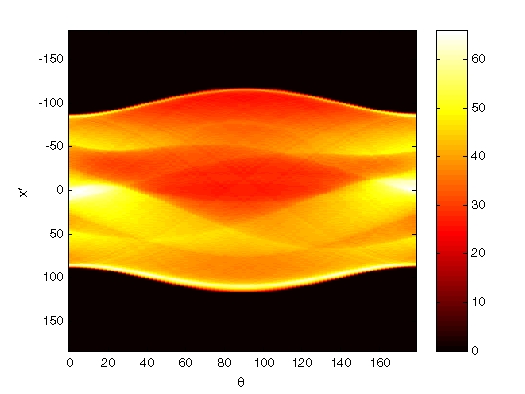
Отметьте, как некоторые функции входного изображения появляются в этом изображении преобразования. Первый столбец в Радоне преобразовывает, соответствует проекции в 0º, который объединяется в вертикальном направлении. Ближайший к центру столбец соответствует проекции в 90º, который объединяется в горизонтальном направлении. Проекция в 90º имеет более широкий профиль, чем проекция в 0º из-за большей вертикальной полуоси наиболее удаленного эллипса фантома.
Восстановите главное фантомное изображение из данных о проекции, созданных на шаге 2, и отобразите результаты.
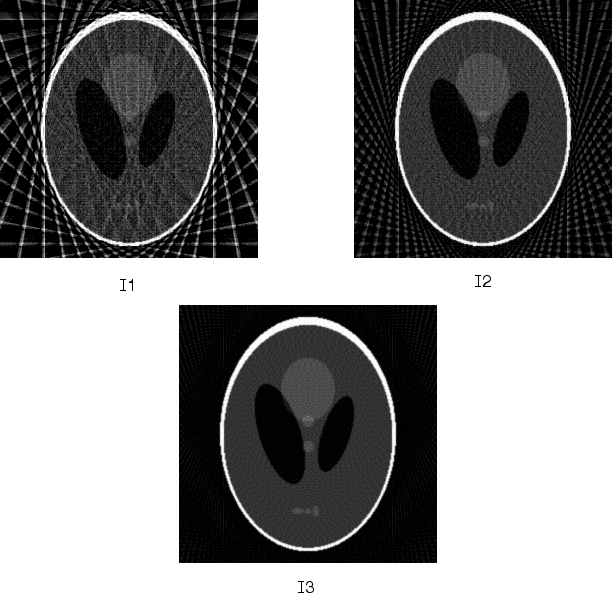
I1 = iradon(R1,10); I2 = iradon(R2,5); I3 = iradon(R3,2); imshow(I1) figure, imshow(I2) figure, imshow(I3)
Следующий рисунок показывает результаты всех трех реконструкций. Заметьте как изображение I1, то, которое было восстановлено только от 18 проекций, является наименее точной реконструкцией. Отобразите I2, то, которое было восстановлено от 36 проекций, лучше, но это все еще не достаточно ясно различить ясно маленькие замещающие знаки в более низком фрагменте изображения. I3, восстановленное использование 90 проекций, наиболее тесно напоминает оригинальное изображение. Заметьте это, когда количество проекций относительно будет мало (как в I1 и I2), реконструкция может включать некоторые артефакты от задней проекции.
Обратные преобразования радона фантома главы Shepp-Логана