Настройте линейную программу, основанную на решателе

Преобразуйте задачу в форму решателя

Этот пример показывает, как преобразовать задачу из математической формы в синтаксис решателя Optimization Toolbox™, используя основанный на решателе подход. Пока задачей является линейная программа, техники применяются ко всем решателям.

Переменные и выражения в проблеме представляют модель работы химического завода из примера в Эдгаре и Химмельблау [1]. Существует два видео, которые описывают проблему.

Математическое Моделирование с Оптимизацией, Часть 1 показывает задачу в графической форме. Это показывает, как сгенерировать математические выражения Образцового Описания из графика.
Моделирование оптимизации, Часть 2: Преобразование в Форму Решателя описывает, как преобразовать эти математические выражения в синтаксис решателя Optimization Toolbox. Это видео показывает, как решить задачу, и как интерпретировать результаты.

Оставшаяся часть этого примера затронута только с преобразованием задачи к синтаксису решателя. Пример сопровождает видео Моделирование Оптимизации, Часть 2: Преобразование в Форму Решателя. Основное различие между видео и примером - то, что этот пример показывает, как использовать именованные переменные или индексные переменные, которые подобны хешированию ключей. Это различие находится в Переменных Объединения В Один Вектор.

Описание модели

Видео Математическое Моделирование с Оптимизацией, Часть 1 предполагает, что один способ преобразовать проблему в математическую форму к:

Получите полную идею проблемы
Идентифицируйте цель (максимизация или минимизация чего-то)
Идентифицируйте (назовите) переменные
Идентифицируйте ограничения
Определите, какими переменными можно управлять
Задайте все величины в математическом обозначении
Проверяйте модель на полноту и правильность

Для значения переменных в этом разделе смотрите видео Математическое Моделирование с Оптимизацией, Частью 1.

Задача оптимизации должна минимизировать целевую функцию согласно всем другим выражениям как ограничения.

Целевая функция:

0.002614 HPS + 0.0239 PP + 0.009825 EP.

Ограничения:

2500 ≤ P1≤ 6250
I1≤ 192,000
C≤ 62,000
I1 - HE1≤ 132,000
I1 = LE1 + HE1 + C
1359.8 I1 = 1267.8 HE1 + 1251.4 LE1 + 192 C + 3413 P1
3000 ≤ P2≤ 9000
I2≤ 244,000
LE2≤ 142,000
I2 = LE2 + HE2
1359.8 I2 = 1267.8 HE2 + 1251.4 LE2 + 3413 P2
HPS = I1 + I2 + BF1
HPS = C + MPS + LPS
LPS = LE1 + LE2 + BF2
MPS = HE1 + HE2 + BF1 - BF2
P1 + P2 + PP≥ 24,550
EP + PP≥ 12,000
MPS≥ 271,536
LPS≥ 100,623
Все переменные положительны.

Метод решения

Чтобы решить задачу оптимизации, возьмите следующие шаги.

Выберите решатель
Объедините переменные в один вектор
Запишите связанные ограничения
Запишите линейные ограничения неравенства
Запишите линейные ограничения равенства
Запишите цель
Решите задачу с linprog
Исследуйте решение

Шаги также показывают в видео Моделировании Оптимизации, Части 2: Преобразование в Форму Решателя.

Выберите решатель

Чтобы найти соответствующий решатель для этой проблемы, консультируйтесь с Таблицей решений Оптимизации. Таблица просит, чтобы вы категоризировали свою проблему типом целевой функции и типами ограничений. Для этой проблемы целевая функция линейна, и ограничения линейны. Таблица решений рекомендует использовать linprog решатель.

Когда вы видите в проблемах, Обработанных Функциями Optimization Toolbox или linprog страница ссылки на функцию, linprog решатель решает задачи формы

\min_{x} f^{T} x таким образом , что {\begin{matrix} A \cdot x \leq b, \\ A e q \cdot x = b e q, \\ l b \leq x \leq u b . \end{matrix}

(1)

^fTx означает вектор-строку из констант f, умножающий вектор-столбец переменных x. Другими словами,
^fTx = f (1) x (1) + f (2) x (2) +... + f (n) x (n),
где n является длиной f.
A x ≤ b представляет линейные неравенства. A является k-by-n матрица, где k является количеством неравенств, и n является количеством переменных (размер x). b является вектором длины k. Для получения дополнительной информации смотрите Линейные Ограничения неравенства.
Aeq x = beq представляет линейные равенства. Aeq является m-by-n матрица, где m является количеством равенств, и n является количеством переменных (размер x). beq является вектором длины m. Для получения дополнительной информации смотрите Линейные Ограничения равенства.
lb ≤ x ≤ ub означает, что каждый элемент в векторном x должен быть больше соответствующего элемента lb и должен быть меньшим, чем соответствующий элемент ub. Для получения дополнительной информации смотрите Связанные Ограничения.

Синтаксис linprog решатель, как показано на его странице ссылки на функцию,

[x fval] = linprog(f,A,b,Aeq,beq,lb,ub);

Входные параметры к linprog решатель является матрицами и векторами в уравнении 1.

Объедините переменные в один вектор

Существует 16 переменных в уравнениях Описания Модели. Поместите эти переменные в один вектор. Именем вектора переменных является x в уравнении 1. Выберите порядок и создайте компоненты x из переменных.

Следующий код создает вектор с помощью массива ячеек имен для переменных.

variables = {'I1','I2','HE1','HE2','LE1','LE2','C','BF1',...
    'BF2','HPS','MPS','LPS','P1','P2','PP','EP'};
N = length(variables); 
% create variables for indexing 
for v = 1:N 
   eval([variables{v},' = ', num2str(v),';']); 
end

Выполнение этих команд создает следующие именованные переменные в вашей рабочей области:

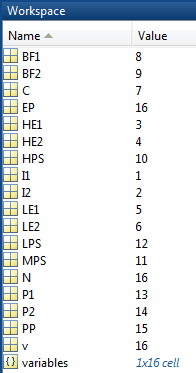
Эти именованные переменные представляют индексы для компонентов x. Вы не должны создавать именованные переменные. Видео Моделирование Оптимизации, Часть 2: Преобразование в Форму Решателя показывает, как решить задачу просто с помощью индексов компонентов x.

Запишите связанные ограничения

Существует четыре переменные с нижними границами, и шесть с верхними границами в уравнениях Описания Модели. Нижние границы:

P1≥ 2500
P2≥ 3000
MPS≥ 271,536
LPS≥ 100,623 .

Кроме того, все переменные положительны, что означает, что у них есть нижняя граница в нуле.

Создайте вектор нижней границы lb как вектор 0, затем добавьте четыре других нижних границы.

lb = zeros(size(variables));
lb([P1,P2,MPS,LPS]) = ...
    [2500,3000,271536,100623];

Переменные с верхними границами:

P1≤ 6250
P2≤ 9000
I1≤ 192,000
I2≤ 244,000
C≤ 62,000
LE2≤ 142000 .

Создайте вектор верхней границы как вектор Inf, затем добавьте эти шесть верхних границ.

ub = Inf(size(variables));
ub([P1,P2,I1,I2,C,LE2]) = ...
   [6250,9000,192000,244000,62000,142000];

Запишите линейные ограничения неравенства

Существует три линейных неравенства в уравнениях Описания Модели:

I1 - HE1≤ 132,000
EP + PP≥ 12,000
P1 + P2 + PP≥ 24,550 .

Для того, чтобы иметь уравнения в форме A x ≤b, поместите все переменные на левую часть неравенства. Все эти уравнения уже имеют ту форму. Убедитесь, что каждое неравенство находится в “меньше, чем” форма путем умножения через на –1 везде, где соответствующий:

I1 - HE1≤ 132,000
-EP - PP≤ -12,000
-P1 - P2 - PP≤ -24,550 .

В вашей рабочей области MATLAB^® создайте A матрица как 3-на-16 нулевая матрица, соответствующая 3 линейным неравенствам с 16 переменными. Создайте b вектор с тремя компонентами.

A = zeros(3,16);
A(1,I1) = 1; A(1,HE1) = -1; b(1) = 132000;
A(2,EP) = -1; A(2,PP) = -1; b(2) = -12000;
A(3,[P1,P2,PP]) = [-1,-1,-1];
b(3) = -24550;

Запишите линейные ограничения равенства

Существует восемь линейных уравнений в уравнениях Описания Модели:

I2 = LE2 + HE2
LPS = LE1 + LE2 + BF2
HPS = I1 + I2 + BF1
HPS = C + MPS + LPS
I1 = LE1 + HE1 + C
MPS = HE1 + HE2 + BF1 - BF2
1359.8 I1 = 1267.8 HE1 + 1251.4 LE1 + 192 C + 3413 P1
1359.8 I2 = 1267.8 HE2 + 1251.4 LE2 + 3413 P2.

Для того, чтобы иметь уравнения в форме Aeq x =beq, поместите все переменные на одну сторону уравнения. Уравнения становятся:

LE2 + HE2 - I2 = 0
LE1 + LE2 + BF2 - LPS = 0
I1 + I2 + BF1 - HPS = 0
C + MPS + LPS - HPS = 0
LE1 + HE1 + C - I1 = 0
HE1 + HE2 + BF1 - BF2 - MPS = 0
1267.8 HE1 + 1251.4 LE1 + 192 C + 3413 P1 - 1359.8 I1 = 0
1267.8 HE2 + 1251.4 LE2 + 3413 P2 - 1359.8 I2 = 0.

Теперь запишите Aeq матрица и beq вектор, соответствующий этим уравнениям. В вашем рабочем пространстве MATLAB создайте Aeq матрица как 8 16 нулевая матрица, соответствуя 8 линейным уравнениям в 16 переменных. Создайте beq вектор с восемью компонентами, всем нулем.

Aeq = zeros(8,16); beq = zeros(8,1);
Aeq(1,[LE2,HE2,I2]) = [1,1,-1];
Aeq(2,[LE1,LE2,BF2,LPS]) = [1,1,1,-1];
Aeq(3,[I1,I2,BF1,HPS]) = [1,1,1,-1];
Aeq(4,[C,MPS,LPS,HPS]) = [1,1,1,-1];
Aeq(5,[LE1,HE1,C,I1]) = [1,1,1,-1];
Aeq(6,[HE1,HE2,BF1,BF2,MPS]) = [1,1,1,-1,-1];
Aeq(7,[HE1,LE1,C,P1,I1]) = [1267.8,1251.4,192,3413,-1359.8];
Aeq(8,[HE2,LE2,P2,I2]) = [1267.8,1251.4,3413,-1359.8];

Запишите цель

Целевая функция

^fTx = 0.002614 HPS + 0.0239 PP + 0.009825 EP.

Запишите это выражение как векторный f из множителей вектора x:

f = zeros(size(variables));
f([HPS PP EP]) = [0.002614 0.0239 0.009825];

Решите задачу с linprog

У вас теперь есть входные параметры, требуемые linprog решатель. Вызовите решатель и распечатайте выходные параметры в отформатированной форме:

options = optimoptions('linprog','Algorithm','dual-simplex');
[x fval] = linprog(f,A,b,Aeq,beq,lb,ub,options);
for d = 1:N
  fprintf('%12.2f \t%s\n',x(d),variables{d}) 
end
fval

Результат:

Optimal solution found.
   136328.74 	I1
   244000.00 	I2
   128159.00 	HE1
   143377.00 	HE2
        0.00 	LE1
   100623.00 	LE2
     8169.74 	C
        0.00 	BF1
        0.00 	BF2
   380328.74 	HPS
   271536.00 	MPS
   100623.00 	LPS
     6250.00 	P1
     7060.71 	P2
    11239.29 	PP
      760.71 	EP

fval =
  1.2703e+03

Исследуйте решение

fval выведите дает наименьшее значение целевой функции при любой допустимой точке.

Вектор решения x точка, где целевая функция имеет наименьшее значение. Заметьте что:

BF1, BF2, и LE1 0, их нижние границы.
I2 244,000, его верхняя граница.
Ненулевые компоненты f вектор
- HPS— 380,328.74
- PP— 11,239.29
- EP— 760.71

Видео Моделирование Оптимизации, Часть 2: Преобразование в Форму Решателя дает интерпретации этих характеристик в терминах исходной проблемы.

Библиография

[1] Эдгар, Томас Ф. и Дэвид М. Химмельблау. Оптимизация химических процессов. McGraw-Hill, Нью-Йорк, 1988.

Документация