Exponenta Banner

phased.UCA

Универсальный круговой массив

расширьте все на странице

Описание

phased.UCA Система object™ создает uniform circular array (UCA). UCA формируется из идентичных элементов датчика, равномерно распределенных вокруг круга.

Вычислить ответ для массива для заданных направлений:

  1. Задайте и настройте свой универсальный круговой массив. Смотрите Конструкцию.

  2. Вызовите step вычислить ответ согласно свойствам phased.UCA. Поведение step характерно для каждого объекта в тулбоксе.

Примечание

Запуск в R2016b, вместо того, чтобы использовать step метод, чтобы выполнить операцию, заданную Системным объектом, можно вызвать объект с аргументами, как будто это была функция. Например, y = step(obj,x) и y = obj(x) выполните эквивалентные операции.

Конструкция

sUCA = phased.UCA создает Системный объект универсального кругового массива (UCA), sUCA, состоя из пяти идентичных изотропных элементов антенны, phased.IsotropicAntennaElement. Элементы равномерно распределены вокруг круга радиуса 0,5 метра.

sUCA = phased.UCA(Name,Value) создает Системный объект, sUCA, с каждым заданным набором имени свойства к заданному значению. Можно задать дополнительные аргументы пары "имя-значение" в любом порядке как (Name1,Value1..., NameN,ValueN).

sUCA = phased.UCA(N,R) создает Системный объект UCA, sUCA, с NumElements набор свойств к N и Radius набор свойств к R. Этот синтаксис создает UCA, состоящий из изотропных элементов антенны, phased.IsotropicAntennaElement.

sUCA = phased.UCA(N,R,Name,Value) создает Системный объект UCA, sUCA, с NumElements набор свойств к N, Radius набор свойств к R, и другой заданный набор имен свойства к заданным значениям.

Свойства

развернуть все

Элемент сенсорной матрицы в виде антенны Phased Array System Toolbox или Системного объекта элемента микрофона. Можно указать элементы антенны, которые делают или не поддерживают поляризацию.

Пример: phased.ShortDipoleAntennaElement()

Количество элементов массива в виде целого числа, больше, чем одно.

Пример 3

Радиус массивов в виде положительной скалярной величины в метрах.

Пример: 2.5

Массив нормальное направление в виде одного из 'x'Y, или 'z'. Элементы UCA лежат в плоскости, ортогональной к массиву нормальное направление. Векторы опорного направления элемента лежат в той же плоскости и указывают радиально исходящий от источника.

Значение свойства ArrayNormalПоложения элемента и направления опорного направления
'x'Элементы массива лежат на yz - плоскость. Все векторы опорного направления элемента лежат в yz - плоскость и точка, исходящая от центра массивов.
'y'Элементы массива лежат на zx - плоскость. Все векторы опорного направления элемента лежат в zx - плоскость и точка, исходящая от центра массивов.
'z'Элементы массива лежат на xy - плоскость. Все векторы опорного направления элемента лежат в xy - плоскость и точка, исходящая от центра массивов.

Пример: 'y'

Сужение элемента или взвешивание в виде скаляра с комплексным знаком, 1 N вектором-строкой или N-by-1 вектор-столбец. Количество N представляет число элементов массива. Заострения, также известные как веса, применяются к каждому элементу датчика в сенсорной матрице и изменяют и амплитуду и фазу полученных данных. Если 'Taper' скаляр, то же значение заострения применяется ко всему элементу. Если 'Taper' вектор, каждое значение заострения применяется к соответствующему элементу датчика.

Пример: [1 2 3 2 1]

Методы

collectPlaneWaveСимулируйте полученные плоские волны
направленностьНаправленность универсального кругового массива
getElementNormalВекторы нормали для элементов массива
getElementPositionПоложения элементов массива
getElementSpacingИнтервал между элементами массива
getNumElementsЧисло элементов в массиве
getTaperЗаострения элемента массива
isPolarizationCapableВозможность поляризации
шаблонПостройте шаблон массивов UCA
patternAzimuthПостройте направленность массивов UCA или шаблон по сравнению с азимутом
patternElevationПостройте направленность массивов UCA или шаблон по сравнению с вертикальным изменением
шагВыведите ответы элементов массива
viewArrayПросмотрите геометрию массивов
Характерный для всех системных объектов
release

Позвольте изменения значения свойства Системного объекта

Примеры

свернуть все

Скрипт Open Live Script

Создайте универсальный круговой массив (UCA) с 11 элементами, имеющий радиус на 1,5 м и действующий на уровне 500 МГц. Массив состоит из элементов антенны короткого диполя. Во-первых, отобразите вертикальную составляющую ответа в 45 азимутах степеней и 0 вертикальных изменениях степеней. Затем постройте направленность вертикального изменения и азимут.

antenna = phased.ShortDipoleAntennaElement(...
    'FrequencyRange',[50e6,1000e6],...
    'AxisDirection','Z');
array = phased.UCA('NumElements',11,'Radius',1.5,'Element',antenna);
fc = 500e6;
ang = [45;0];
resp = array(fc,ang);
disp(resp.V)
   -1.2247
   -1.2247
   -1.2247
   -1.2247
   -1.2247
   -1.2247
   -1.2247
   -1.2247
   -1.2247
   -1.2247
   -1.2247

Отобразите шаблон направленности азимута на уровне 500 МГц для углов азимута между-180 и 180 градусами.

c = physconst('LightSpeed');
pattern(array,fc,[-180:180],0,'Type','directivity','PropagationSpeed',c)

Отобразите шаблон направленности вертикального изменения на уровне 500 МГц для углов вертикального изменения между-90 и 90 градусами.

pattern(array,fc,[0],[-90:90],'Type','directivity','PropagationSpeed',c)

Алгоритмы

UCA формируется из N идентичные элементы датчика, равномерно распределенные вокруг круга радиуса R. Круг находится в xy - плоскость системы локальной координаты, источник которой находится в центре круга. Положения элементов заданы относительно системы координат локального массива. Круговой массив находится в xy - плоскость системы координат. Нормальное к плоскости UCA простирается вдоль положительного z - ось. Элементы ориентированы так, чтобы их основные направления ответа (нормали) указали радиально исходящий в xy - плоскость.

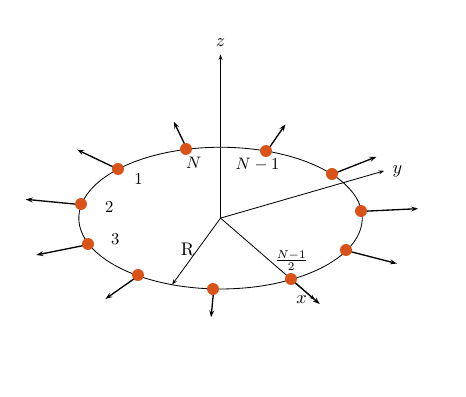
Если число элементов массива является нечетным, средний элемент находится на x - ось. Если число элементов является четным, средняя точка между двумя средними элементами находится на x - ось. Для массива элементов N углом азимута положения элемента nth дают

φn=(−(N−1)/2+n−1)⋅360/N    n=1,…,N

Угол азимута задан как угол, в xy - плоскости, от x - оси к y - ось. Угол вертикального изменения задан как угол от xy - плоскости к z - ось. Угловое расстояние между любыми двумя смежными элементами является степенями 360/N. Угловые значения азимута в градусах. Углы вертикального изменения для всех элементов массива являются нулем.

Ссылки

[1] Brookner, E., Радарная Технология редактора. Лексингтон, MA: LexBook, 1996.

[2] Деревья фургона, H. Оптимальная Обработка матриц. Нью-Йорк: Wiley-межнаука, 2002, стр 274–304.

Расширенные возможности

Смотрите также

| | | | | | | | |

Темы

Представленный в R2015a

Документация Phased Array System Toolbox
Поддержка