Создайте пустой iconnect (соединение) объекты
H = iconnect
Соединительные объекты (класс iconnect) альтернатива sysic, и используются, чтобы создать комплексные соединения неопределенных матриц и систем.
iconnect объект имеет 3 поля, которые будут установлены пользователем, Inputвывод и Equationвходной параметр и Output icsignal объекты, в то время как Equation.is массив ячеек ограничений равенства (использующий equate) на icsignal объекты. Если они заданы, затем System свойство является моделью ввода/вывода, подразумеваемой ограничениями в Equation. связь переменных задана в Input и Output.
iconnect может использоваться, чтобы создать матрицу передачи M как описано в следующей фигуре.
![]()
Создайте три скалярных icsignal: r, e и y. Создайте пустой iconnect объект, M. Задайте выход соединения, чтобы быть [e; y], и вход, чтобы быть r. Задайте два ограничения среди переменных: e = r-y, и y = (2/s) e. Получите представление передаточной функции отношения между входом (r) и выход [e; y].
r = icsignal(1);
e = icsignal(1);
y = icsignal(1);
M = iconnect;
M.Input = r;
M.Output = [e;y];
M.Equation{1} = equate(e,r-y);
M.Equation{2} = equate(y,tf(2,[1 0])*e);
tf(M.System)
Передаточные функции от входа до выходных параметров
s
#1: -----
s + 2
2
#2: -----
s + 2
Путем не явным образом представления e, это может быть сделано более кратко только с одним ограничением равенства.
r = icsignal(1);
y = icsignal(1);
N = iconnect;
N.Input = r;
N.Output = [r-y;y];
N.Equation{1} = equate(y,tf(2,[1 0])*(r-y));
tf(N.System)
Вы создали те же передаточные функции от входа до выходных параметров.
s
#1: -----
s + 2
2
#2: -----
s + 2
Можно также задать неопределенные, многомерные соединения с помощью iconnect. Рассмотрите два неопределенных ограничения двигателя/генератора среди 4 переменных [V;I;T;W], V-R*I-K*W=0, и T=K*I. Найдите неопределенный 2x2 матричный B так, чтобы [V;T] = B*[W;I].
R = ureal('R',1,'Percentage',[-10 40]);
K = ureal('K',2e-3,'Percentage',[-30 30]);
V = icsignal(1);
I = icsignal(1);
T = icsignal(1);
W = icsignal(1);
M = iconnect;
M.Input = [W;I];
M.Output = [V;T];
M.Equation{1} = equate(V-R*I-K*W,iczero(1));
M.Equation{2} = equate(T,K*I);
B = M.System
UMAT: 2 Rows, 2 Columns
K: real, nominal = 0.002, variability = [-30 30]%, 2 occurrences
R: real, nominal = 1, variability = [-10 40]%, 1 occurrence
B.NominalValue
ans =
0.0020 1.0000
0 0.0020
Простое системное соединение, идентичное системе, проиллюстрировано в sysic страницы с описанием. Считайте с тремя входами, 2D выходную матрицу пространства состояний T,
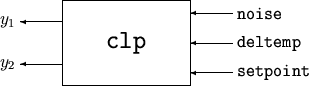
который имеет внутреннюю структуру
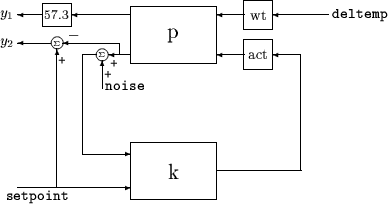
P = rss(3,2,2);
K = rss(1,1,2);
A = rss(1,1,1);
W = rss(1,1,1);
M = iconnect;
noise = icsignal(1);
deltemp = icsignal(1);
setpoint = icsignal(1);
yp = icsignal(2);
rad2deg = 57.3
rad2deg =
57.3000
M.Equation{1} = equate(yp,P*[W*deltemp;A*K*[noise+yp(2);setpoint]]);
M.Input = [noise;deltemp;setpoint];
M.Output = [rad2deg*yp(1);setpoint-yp(2)];
T = M.System;
size(T)
State-space model with 2 outputs, 3 inputs, and 6 states.
Синтаксис для iconnect объекты и icsignals очень гибок. Без ухода можно создать неэффективный (т.е. неминимальный) представления, где размерность состояния соединения больше суммы размерностей состояния компонентов. Это в отличие от sysic. В sysic, синтаксис раньше задавал входные параметры к системам (input_to_ListedSubSystemName переменная), обеспечивает вас, чтобы включать каждую подсистему соединения только однажды в уравнениях. Следовательно, соединения, сформированные с sysic покомпонентно минимальны. Таким образом, размерность состояния соединения равняется сумме размерностей состояния компонентов.
Каждое уравнение представляет ограничение равенства среди переменных. Вы выбираете переменные ввода и вывода и imp2exp функция делает неявное отношение между ними явным.