Вычислите L 2 нормы системы непрерывного времени в обратной связи с системой дискретного времени
[gaml,gamu] = sdhinfnorm(sdsys,k) [gaml,gamu] = sdhinfnorm(sdsys,k,delay) [gaml,gamu] = sdhinfnorm(sdsys,k,delay,tol)
[gaml,gamu] = sdhinfnorm(sdsys,k) вычисляет L 2 вызванных нормы объекта LTI непрерывного времени, sdsys, в обратной связи с контроллером дискретного времени, k, соединенный через идеальный сэмплер и нулевой порядок содержат (см. фигуру ниже). sdsys должно быть строго соответствующим, таким, что постоянное усиление обратной связи должно быть нулем. Выходные параметры, gamu и gaml, верхние и нижние границы на вызванном L 2 нормы выборочных данных система с обратной связью.
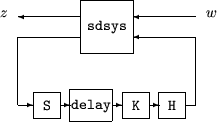
[gaml,gamu] = sdhinfnorm(sdsys,k,h,delay) включает входной параметр delay. delay неотрицательное целое число, сопоставленное с количеством вычислительных задержек контроллера. Значение по умолчанию задержки 0.
[gaml,gamu] = sdhinfnorm(sdsys,k,h,delay,tol) включает входной параметр, tol, который задает различие между верхними и нижними границами, когда поиск завершает работу. Значение по умолчанию tol 0.001.
Рассмотрите разомкнутый цикл, передаточная функция непрерывного времени p = 30/s(s+30) и непрерывное время controller k = 4/(s+4). Система непрерывного времени с обратной связью имеет пиковую величину через частоту 1.
p = ss(tf(30,[1 30])*tf([1],[1 0]));
k = ss(tf(4,[1 4]));
cl = feedback(p,k);
norm(cl,'inf')
ans =
1
Первоначально контроллер должен быть реализован на уровне частоты дискретизации 1,5 Гц. Норма выборочных данных системы с обратной связью с контроллером дискретного времени 1.0.
kd = c2d(k,0.75,'zoh');
[gu,gl] = sdhinfnorm([1; 1]*p*[1 1],-kd);
[gu gl]
ans =
3.7908 3.7929
Из-за значительных различий в норме между непрерывным временем и выборочными данными система с обратной связью, частота дискретизации контроллера увеличена с 1,5 Гц до 5 Гц. Норма выборочных данных новой системы с обратной связью 3.79.
kd = c2d(k,0.2,'zoh');
[gu,gl] = sdhinfnorm([1; 1]*p*[1 1],-kd);
[gu gl]
ans =
1.0044 1.0049
sdhinfnorm изменения использования формул описаны в статье Бэмиха и Пирсона получить эквивалентную систему дискретного времени. (Эти изменения сделаны, чтобы улучшить числовое создание условий алгоритмов.) Предварительный шаг должен определить, меньше ли норма системы непрерывного времени за один период выборки свободно данного значения. Это требует поиска и является, в вычислительном отношении, относительно дорогим шагом.
Bamieh, степень бакалавра гуманитарных наук и Дж.Б. Пирсон, “Общие рамки для Линейных Периодических Систем с Приложениями к Управлению Выборочных данных”, Транзакции IEEE на Автоматическом управлении, издании AC-37, 1992, стр 418-435.