Карта порядок-об/мин анализа порядка
map = rpmordermap(x,fs,rpm)map, это следует из выполнения анализа порядка входного вектора, xX измеряется в наборе rpm из скоростей вращения, выраженных в оборотах в минуту. fs частота дискретизации измерения в Гц. Каждый столбец map содержит среднеквадратичные (RMS) амплитудные оценки подарка порядков в каждом rpm значение. rpmordermap передискретизирует x к постоянному уровню выборок на цикл и использованию кратковременное преобразование Фурье, чтобы анализировать спектральное содержимое передискретизируемого сигнала.
map = rpmordermap(___,Name,Value)Name,Value пары в дополнение к входным параметрам в предыдущих синтаксисах.
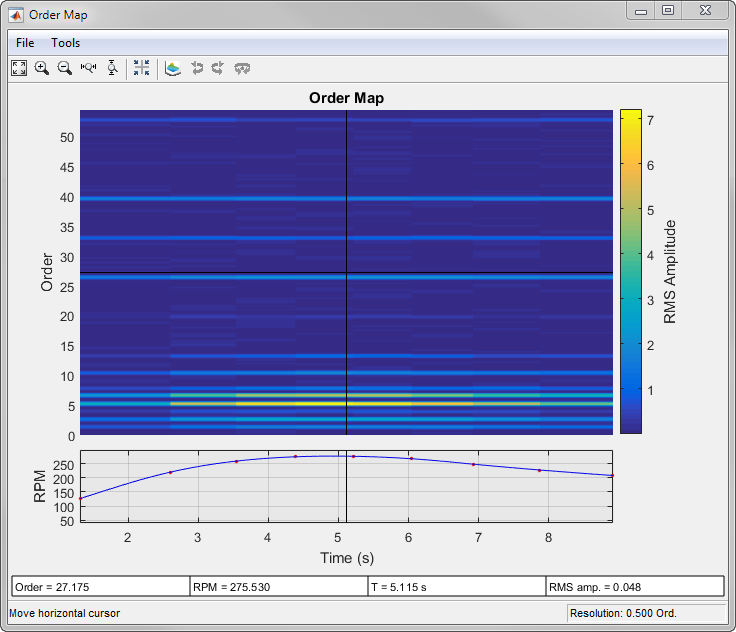
rpmordermap(___) без выходных аргументов строит карту порядка как функцию скорости вращения и время на интерактивной фигуре.
Прикажите, чтобы анализ был исследованием колебаний во вращающихся системах, которые следуют из самого вращения. Частоты этих колебаний часто пропорциональны скорости вращения. Коэффициенты пропорциональности являются порядками.
Скорость вращения обычно измеряется независимо и изменяется со временем при большинстве экспериментальных условий. Соответствующий анализ вызванных вращением колебаний требует передискретизации и интерполяции измеренного сигнала достигнуть постоянного количества выборок на цикл. Посредством этого процесса компоненты сигнала, частоты которых являются постоянными множителями скорости вращения, преобразовывают в постоянные тоны. Преобразование уменьшает смазывание спектральных компонентов, которое происходит, когда частота изменяется быстро со временем.
rpmordermap функция выполняет эти шаги:
Использование cumtrapz оценить угол фазы как интеграл времени скорости вращения:
Использование resample сверхдискретизировать и фильтр lowpass сигнал. Этот шаг позволяет функции интерполировать сигнал в непроизведенных моментах времени, не искажая высокочастотных компонентов. rpmordermap сверхдискретизировал сигнал фактором 15.
Использование interp1 интерполировать сверхдискретизированный сигнал линейно на регулярную координатную сетку в области фазы. Самый высокий доступный порядок в измерении фиксируется частотой дискретизации и самой высокой скоростью вращения, достигнутой системой:
Чтобы получить этот самый высокий порядок точно, необходимо произвести сигнал в дважды O макс., по крайней мере. Для лучших результатов, rpmordermap сверхдискретизировал дополнительным фактором 4. Получившаяся доменная фазой частота дискретизации, fp,
Разрешение порядка по умолчанию, r,
Использование spectrogram вычислить кратковременное преобразование Фурье (STFT) интерполированного сигнала. По умолчанию функция делит сигнал на L - демонстрационные сегменты и окна каждый из них с окном с плоской вершиной. Существуют
выборки перекрытия между смежными сегментами, где перекрытие p задано с помощью 'OverlapPercent' пара "имя-значение" и значения по умолчанию к 50%. Длина ДПФ установлена в L. Разрешение связано с частотой дискретизации и длиной сегмента через
где k является эквивалентной шумовой полосой окна, как реализовано в enbw. Настройте разрешение, чтобы дифференцировать близко расположенные порядки. Меньшие значения r требуют больших длин сегмента. Если необходимо достигнуть данного разрешения, убедитесь, что сигнал имеет достаточно выборок.
Красные точки в об/мин-по-сравнению-с-разовым строят в нижней части интерактивного rpmordermap окно соответствует правому краю каждого оконного сегмента. Синяя линия в графике является сигналом об/мин, чертившим как функция времени:
[1] Брандт, Андерс. Шум и анализ вибрации: анализ сигнала и экспериментальные процедуры. Чичестер, Великобритания: John Wiley & Sons, 2011.
orderspectrum | ordertrack | orderwaveform | rpmfreqmap | rpmtrack | spectrogram | tachorpm