Смоделировать дифференциальное уравнение
x´ = –2x (t) +u (t),
где u (t) является прямоугольной волной с амплитудой 1 и частота 1 рад/секунда, используйте блок интегратора и блок усиления. Блок Integrator интегрирует свой вход x´, чтобы произвести x. Другие блоки, необходимые в этой модели включать блок Gain и блок Sum. Чтобы сгенерировать прямоугольную волну, используйте блок Signal Generator и выберите форму Прямоугольной волны, но измените модули по умолчанию в радианы/секунда. Снова, просмотрите выход с помощью блока Scope. Соберите блоки и задайте усиление.
В этой модели, чтобы инвертировать направление блока Gain, выбирают блок, затем на вкладке Format, нажимают лево-право Flip
. Чтобы создать ответвление из выхода блока Integrator с блоком Gain, удерживайте клавишу CTRL при разграничивании. Для получения дополнительной информации смотрите Ветвь Связь.
Теперь можно соединить все блоки.
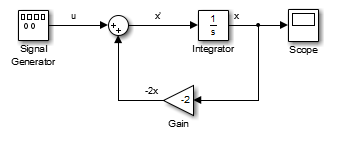
Важной концепцией в этой модели является цикл, который включает блок Sum, блок Integrator и блок Gain. В этом уравнении x является выход блока Integrator. Это - также вход с блоками, которые вычисляют x´, на котором это базируется. Это отношение реализовано с помощью цикла.
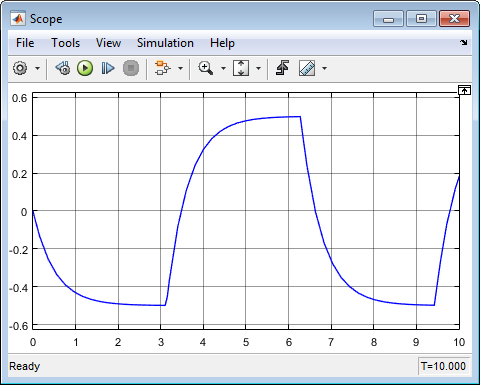
Осциллограф отображает x на каждом временном шаге. Для симуляции, длящейся 10 секунд, выглядит так выход:
Уравнение, которое вы смоделировали в этом примере, может также быть выражено как передаточная функция. Модель использует блок Transfer Fcn, который принимает u как вход и выходные параметры x. Так, блок реализует x/u. Если вы заменяете sx x´ в вышеупомянутом уравнении, вы добираетесь
sx = –2x + u.
Решение для x дает
x = u / (s + 2)
или,
x/u = 1 / (s + 2).
Блок Transfer Fcn использует параметры, чтобы задать коэффициенты знаменателя и числитель. В этом случае числителем является 1 и знаменателем является s+2. Задайте оба условия с должности векторов коэффициентов последовательно уменьшающихся степеней s.
В этом случае числителем является [1] (или только 1) и знаменателем является [1 2].
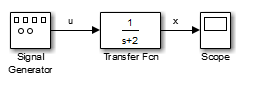
Результаты этой симуляции идентичны тем из предыдущей модели.
