Исследование остаточных значений для Model Verification

Можно исследовать stats структура, которая возвращена обоими nlmefit и nlmefitsa, определить качество вашей модели. stats структура содержит поля со взвешенными остаточными значениями условного выражения (cwres поле), и индивидуум взвесил остаточные значения (iwres поле . Поскольку модель принимает, что остаточные значения нормально распределены, можно исследовать остаточные значения, чтобы видеть, как хорошо это предположение содержит.

Этот пример генерирует синтетические данные с помощью нормальных распределений. Это показывает, как подходящие статистические данные смотрят:

Хороший при тестировании против того же типа модели, как генерирует данные
Плохой, когда протестировано против неправильных моделей данных

Инициализируйте 2D модель 100 индивидуумами:

nGroups = 100; % 100 Individuals
nlmefun = @(PHI,t)(PHI(:,1)*5 + PHI(:,2)^2.*t); % Regression fcn
REParamSelect = [1  2]; % Both Parameters have random effect
errorParam = .03; 
beta0 = [ 1.5  5]; % Parameter means
psi = [ 0.35  0; ...  % Covariance Matrix
       0   0.51 ];
time =[0.25;0.5;0.75;1;1.25;2;3;4;5;6];
nParameters = 2;
rng(0,'twister') % for reproducibility

Сгенерируйте данные для подбора кривой пропорциональной ошибочной моделью:

b_i = mvnrnd(zeros(1, numel(REParamSelect)), psi, nGroups);
individualParameters = zeros(nGroups,nParameters);
individualParameters(:, REParamSelect) = ...
     bsxfun(@plus,beta0(REParamSelect), b_i);

groups = repmat(1:nGroups,numel(time),1);
groups = vertcat(groups(:));

y = zeros(numel(time)*nGroups,1);
x = zeros(numel(time)*nGroups,1);
for i = 1:nGroups
    idx = groups == i;
    f = nlmefun(individualParameters(i,:), time);
    % Make a proportional error model for y:
    y(idx) = f + errorParam*f.*randn(numel(f),1);
    x(idx) = time;
end

P = [ 1 0 ; 0 1 ];

Соответствуйте данным с помощью той же модели функции и ошибки регрессии в качестве генератора модели:
```
[~,~,stats] = nlmefit(x,y,groups, ...
    [],nlmefun,[1 1],'REParamsSelect',REParamSelect,...
    'ErrorModel','Proportional','CovPattern',P);
```

Создайте стандартную программу графического вывода путем копирования следующего функционального определения и создания файла plotResiduals.m на вашем пути MATLAB^®:

function plotResiduals(stats)
pwres = stats.pwres;
iwres = stats.iwres;
cwres = stats.cwres;
figure
subplot(2,3,1);
normplot(pwres); title('PWRES')
subplot(2,3,4);
createhistplot(pwres);

subplot(2,3,2);
normplot(cwres); title('CWRES')
subplot(2,3,5);
createhistplot(cwres);

subplot(2,3,3);
normplot(iwres); title('IWRES')
subplot(2,3,6);
createhistplot(iwres); title('IWRES')

function createhistplot(pwres)
h = histogram(pwres);

% x is the probability/height for each bin
x = h.Values/sum(h.Values*h.BinWidth)

% n is the center of each bin
n = h.BinEdges + (0.5*h.BinWidth)
n(end) = [];

bar(n,x);
ylim([0 max(x)*1.05]);
hold on;
x2 = -4:0.1:4;
f2 = normpdf(x2,0,1);
plot(x2,f2,'r');
end

end

Постройте остаточные значения с помощью plotResiduals функция:
```
plotResiduals(stats);
```
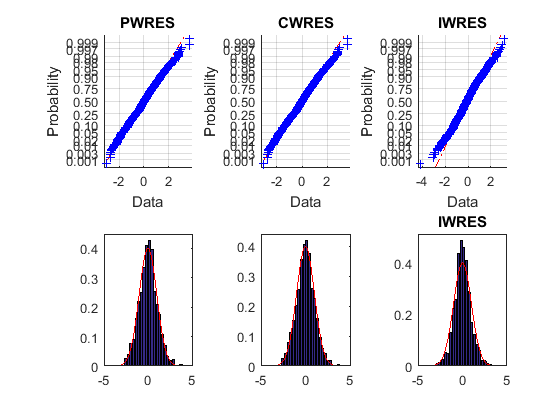
Верхние графики вероятности выглядят прямыми, означая, что остаточные значения нормально распределены. Нижние графики гистограммы совпадают с наложенным нормальным графиком плотности. Таким образом, можно прийти к заключению, что ошибочная модель совпадает с данными.
Для сравнения, соответствуют данные с помощью постоянной ошибочной модели, вместо пропорциональной модели, которая создала данные:
```
[~,~,stats] = nlmefit(x,y,groups, ...
    [],nlmefun,[0 0],'REParamsSelect',REParamSelect,...
    'ErrorModel','Constant','CovPattern',P);
plotResiduals(stats);
```
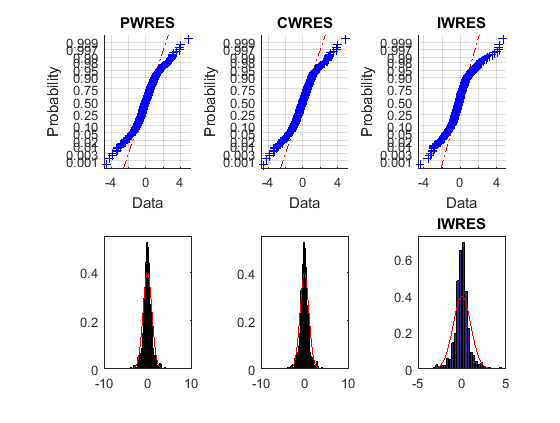
Верхние графики вероятности не являются прямыми, указывая, что остаточные значения не нормально распределены. Нижние графики гистограммы справедливо близко к наложенным нормальным графикам плотности.
Для другого сравнения соответствуйте данным к различной структурной модели, чем созданный данные:
```
nlmefun2 = @(PHI,t)(PHI(:,1)*5 + PHI(:,2).*t.^4);
[~,~,stats] = nlmefit(x,y,groups, ...
    [],nlmefun2,[0 0],'REParamsSelect',REParamSelect,...
    'ErrorModel','constant', 'CovPattern',P);
plotResiduals(stats);
```
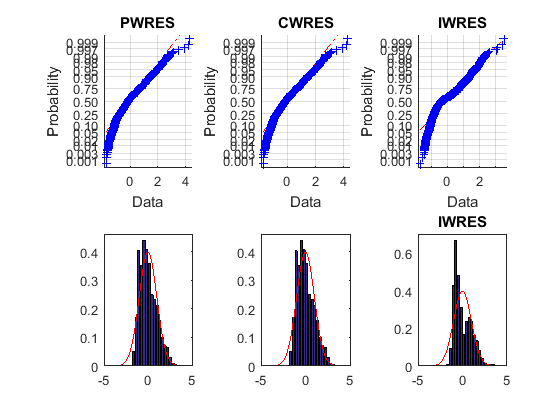
Мало того, что верхние графики вероятности не являются прямыми, но и график гистограммы, вполне скашивается по сравнению с наложенной нормальной плотностью. Эти остаточные значения не нормально распределены, и не совпадают с моделью.

Документация

Исследование остаточных значений для Model Verification

Документация Statistics and Machine Learning Toolbox

Поддержка