fitlda

Подходящая модель скрытого выделения Дирихле (LDA)

Синтаксис

mdl = fitlda(bag,numTopics)

mdl = fitlda(counts,numTopics)

mdl = fitlda(___,Name,Value)

Описание

Модель скрытого выделения Дирихле (LDA) является моделью темы, которая обнаруживает базовые темы в наборе документов и выводит вероятности слова в темах. Если модель была подходящим использованием мешка n модели граммов, то программное обеспечение обрабатывает N-граммы как отдельные слова.

пример

mdl = fitlda(bag,numTopics) подбирает модель LDA с numTopics темы к сумке слов или мешку n модели bag граммов.

пример

mdl = fitlda(counts,numTopics) подбирает модель LDA к документам, представленным матрицей подсчета частот.

mdl = fitlda(___,Name,Value) задает дополнительные опции с помощью одного или нескольких аргументов пары "имя-значение".

Примеры

свернуть все

Подбирайте модель LDA

Скрипт Open Live Script

Чтобы воспроизвести результаты в этом примере, установите rng к 'default'.

rng('default')

Загрузите данные в качестве примера. Файл sonnetsPreprocessed.txt содержит предварительно обработанные версии сонетов Шекспира. Файл содержит один сонет на строку со словами, разделенными пробелом. Извлеките текст из sonnetsPreprocessed.txt, разделите текст в документы в символах новой строки, и затем маркируйте документы.

filename = "sonnetsPreprocessed.txt";
str = extractFileText(filename);
textData = split(str,newline);
documents = tokenizedDocument(textData);

Создайте модель сумки слов использование bagOfWords.

bag = bagOfWords(documents)

bag = 
  bagOfWords with properties:

          Counts: [154x3092 double]
      Vocabulary: [1x3092 string]
        NumWords: 3092
    NumDocuments: 154

Подбирайте модель LDA с четырьмя темами.

numTopics = 4;
mdl = fitlda(bag,numTopics)

Initial topic assignments sampled in 0.072524 seconds.
=====================================================================================
| Iteration  |  Time per  |  Relative  |  Training  |     Topic     |     Topic     |
|            | iteration  | change in  | perplexity | concentration | concentration |
|            | (seconds)  |   log(L)   |            |               |   iterations  |
=====================================================================================
|          0 |       0.00 |            |  1.215e+03 |         1.000 |             0 |
|          1 |       0.01 | 1.0482e-02 |  1.128e+03 |         1.000 |             0 |
|          2 |       0.02 | 1.7190e-03 |  1.115e+03 |         1.000 |             0 |
|          3 |       0.01 | 4.3796e-04 |  1.118e+03 |         1.000 |             0 |
|          4 |       0.01 | 9.4193e-04 |  1.111e+03 |         1.000 |             0 |
|          5 |       0.01 | 3.7079e-04 |  1.108e+03 |         1.000 |             0 |
|          6 |       0.01 | 9.5777e-05 |  1.107e+03 |         1.000 |             0 |
=====================================================================================

mdl = 
  ldaModel with properties:

                     NumTopics: 4
             WordConcentration: 1
            TopicConcentration: 1
      CorpusTopicProbabilities: [0.2500 0.2500 0.2500 0.2500]
    DocumentTopicProbabilities: [154x4 double]
        TopicWordProbabilities: [3092x4 double]
                    Vocabulary: [1x3092 string]
                    TopicOrder: 'initial-fit-probability'
                       FitInfo: [1x1 struct]

Визуализируйте темы с помощью облаков слова.

figure
for topicIdx = 1:4
    subplot(2,2,topicIdx)
    wordcloud(mdl,topicIdx);
    title("Topic: " + topicIdx)
end

Подбирайте модель LDA к матрице для подсчета количества слов

Скрипт Open Live Script

Подбирайте модель LDA к набору документов, представленных матрицей для подсчета количества слов.

Чтобы воспроизвести результаты этого примера, установите rng к 'default'.

rng('default')

Загрузите данные в качестве примера. sonnetsCounts.mat содержит матрицу подсчетов слов и соответствующий словарь предварительно обработанных версий сонетов Шекспира. Значение counts(i,j) соответствует числу раз jслово th словаря появляется в iдокумент th.

load sonnetsCounts.mat
size(counts)

ans = 1×2

         154        3092

Подбирайте модель LDA с 7 темами. Чтобы подавить многословный выход, установите 'Verbose' к 0.

numTopics = 7;
mdl = fitlda(counts,numTopics,'Verbose',0);

Визуализируйте несколько смесей темы с помощью сложенных столбчатых диаграмм. Визуализируйте смеси темы первых трех входных документов.

topicMixtures = transform(mdl,counts(1:3,:));
figure
barh(topicMixtures,'stacked')
xlim([0 1])
title("Topic Mixtures")
xlabel("Topic Probability")
ylabel("Document")
legend("Topic "+ string(1:numTopics),'Location','northeastoutside')

Предскажите главные темы LDA документов

Скрипт Open Live Script

Чтобы воспроизвести результаты в этом примере, установите rng к 'default'.

rng('default')

filename = "sonnetsPreprocessed.txt";
str = extractFileText(filename);
textData = split(str,newline);
documents = tokenizedDocument(textData);

Создайте модель сумки слов использование bagOfWords.

bag = bagOfWords(documents)

bag = 
  bagOfWords with properties:

          Counts: [154x3092 double]
      Vocabulary: [1x3092 string]
        NumWords: 3092
    NumDocuments: 154

Подбирайте модель LDA с 20 темами.

numTopics = 20;
mdl = fitlda(bag,numTopics)

Initial topic assignments sampled in 0.061742 seconds.
=====================================================================================
| Iteration  |  Time per  |  Relative  |  Training  |     Topic     |     Topic     |
|            | iteration  | change in  | perplexity | concentration | concentration |
|            | (seconds)  |   log(L)   |            |               |   iterations  |
=====================================================================================
|          0 |       0.14 |            |  1.159e+03 |         5.000 |             0 |
|          1 |       0.07 | 5.4884e-02 |  8.028e+02 |         5.000 |             0 |
|          2 |       0.05 | 4.7400e-03 |  7.778e+02 |         5.000 |             0 |
|          3 |       0.06 | 3.4597e-03 |  7.602e+02 |         5.000 |             0 |
|          4 |       0.07 | 3.4662e-03 |  7.430e+02 |         5.000 |             0 |
|          5 |       0.07 | 2.9259e-03 |  7.288e+02 |         5.000 |             0 |
|          6 |       0.05 | 6.4180e-05 |  7.291e+02 |         5.000 |             0 |
=====================================================================================

mdl = 
  ldaModel with properties:

                     NumTopics: 20
             WordConcentration: 1
            TopicConcentration: 5
      CorpusTopicProbabilities: [1x20 double]
    DocumentTopicProbabilities: [154x20 double]
        TopicWordProbabilities: [3092x20 double]
                    Vocabulary: [1x3092 string]
                    TopicOrder: 'initial-fit-probability'
                       FitInfo: [1x1 struct]

Предскажите главные темы для массива новых документов.

newDocuments = tokenizedDocument([
    "what's in a name? a rose by any other name would smell as sweet."
    "if music be the food of love, play on."]);
topicIdx = predict(mdl,newDocuments)

topicIdx = 2×1

    19
     8

Визуализируйте предсказанные темы с помощью облаков слова.

figure
subplot(1,2,1)
wordcloud(mdl,topicIdx(1));
title("Topic " + topicIdx(1))
subplot(1,2,2)
wordcloud(mdl,topicIdx(2));
title("Topic " + topicIdx(2))

Входные параметры

свернуть все

`bag` — Модель Input
`bagOfWords` возразите | `bagOfNgrams` объект

Введите сумку слов или мешок n модели граммов в виде bagOfWords возразите или bagOfNgrams объект. Если bag bagOfNgrams объект, затем функция обрабатывает каждую n-грамму как отдельное слово.

`numTopics` — Количество тем
положительное целое число

Количество тем в виде положительного целого числа. Для примера, показывающего, как выбрать количество тем, смотрите, Выбирают Number of Topics for LDA Model.

Пример: 200

`counts` — Подсчет частот слов
матрица неотрицательных целых чисел

Подсчет частот слов в виде матрицы неотрицательных целых чисел. Если вы задаете 'DocumentsIn' быть 'rows', затем значение counts(i,j) соответствует числу раз, j th слово словаря появляется в i th документ. В противном случае, значение counts(i,j) соответствует числу раз, i th слово словаря появляется в j th документ.

Аргументы в виде пар имя-значение

Задайте дополнительные разделенные запятой пары Name,Value аргументы. Name имя аргумента и Value соответствующее значение. Name должен появиться в кавычках. Вы можете задать несколько аргументов в виде пар имен и значений в любом порядке, например: Name1, Value1, ..., NameN, ValueN.

Пример: 'Solver','avb' задает, чтобы использовать аппроксимированного вариационного Бейеса в качестве решателя.

Опции решателя

свернуть все

`'Solver'` — Решатель для оптимизации
`'cgs'` (значение по умолчанию) | `'savb'` | `'avb'` | `'cvb0'`

Решатель для оптимизации в виде разделенной запятой пары, состоящей из 'Solver' и одно из следующего:

Стохастический решатель

'savb' – Используйте стохастический аппроксимированный вариационный Байесов [1] [2]. Этот решатель подходит лучше всего для больших наборов данных и может подбирать хорошую модель в меньшем количестве передач данных.

Пакетные решатели

'cgs' – Используйте свернутый Гиббс, производящий [3]. Этот решатель может быть более точным за счет занимания больше времени, чтобы запуститься. resume функция не делает моделей поддержки, снабженных CGS.
'avb' – Используйте аппроксимированного вариационного Бейеса [4]. Этот решатель обычно запускается более быстро, чем свернутый Гиббс, производящий, и свернул вариационного Бейеса, но может быть менее точным.
'cvb0' – Используйте свернутого вариационного Бейеса, нулевой [4] [5] порядка. Этот решатель может быть более точным, чем аппроксимированный вариационный Бейес за счет занимания больше времени, чтобы запуститься.

Для примера, показывающего, как сравнить решатели, смотрите, Сравнивают Решатели LDA.

Пример: 'Solver','savb'

`'LogLikelihoodTolerance'` — Относительный допуск на логарифмической правдоподобности
0.0001 (значение по умолчанию) | положительная скалярная величина

Относительный допуск на логарифмической правдоподобности в виде разделенной запятой пары, состоящей из 'LogLikelihoodTolerance' и положительная скалярная величина. Оптимизация завершает работу, когда этот допуск достигнут.

Пример: 'LogLikelihoodTolerance',0.001

`'FitTopicProbabilities'` — Опция для подходящих корпусных вероятностей темы
`true` (значение по умолчанию) | `false`

Опция для подходящей концентрации темы в виде разделенной запятой пары, состоящей из 'FitTopicConcentration' и любой true или false.

Функция соответствует предшествующему Дирихле $α = α_{0} (\begin{matrix} p_{1} & p_{2} & \dots & p_{K} \end{matrix})$ на смесях темы, где $α_{0}$ концентрация темы и $p_{1}, \dots, p_{K}$ корпусные вероятности темы, которые суммируют к 1.

Пример: 'FitTopicProbabilities',false

Типы данных: логический

`'FitTopicConcentration'` — Опция для подходящей концентрации темы
`true` | `false`

Для пакета решатели 'cgs', 'avb', и 'cvb0', значение по умолчанию для FitTopicConcentration true. Для стохастического решателя 'savb', значением по умолчанию является false.

Пример: 'FitTopicConcentration',false

Типы данных: логический

`'InitialTopicConcentration'` — Первоначальная оценка концентрации темы
`numTopics/4` (значение по умолчанию) | неотрицательный скаляр

Первоначальная оценка концентрации темы в виде разделенной запятой пары, состоящей из 'InitialTopicConcentration' и неотрицательный скаляр. Функция устанавливает концентрацию на тему к TopicConcentration/NumTopics. Для получения дополнительной информации смотрите Скрытое Выделение Дирихле.

Пример: 'InitialTopicConcentration',25

`'TopicOrder'` — Порядок темы
`'initial-fit-probability'` (значение по умолчанию) | `'unordered'`

Порядок темы в виде одного из следующего:

'initial-fit-probability' – Сортировка тем корпусными вероятностями темы входного набора документа (CorpusTopicProbabilities свойство.
'unordered' – Не сортируйте темы.

`'WordConcentration'` — Концентрация Word
1 (значение по умолчанию) | неотрицательный скаляр

Концентрация Word в виде разделенной запятой пары, состоящей из 'WordConcentration' и неотрицательный скаляр. Программное обеспечение устанавливает Дирихле, предшествующий по темам (вероятности слова на тему) быть симметричным параметром распределения Дирихле со значением WordConcentration/numWords, где numWords размер словаря входных документов. Для получения дополнительной информации смотрите Скрытое Выделение Дирихле.

`'DocumentsIn'` — Ориентация документов
`'rows'` (значение по умолчанию) | `'columns'`

Ориентация документов в матрице для подсчета количества слов в виде разделенной запятой пары, состоящей из 'DocumentsIn' и одно из следующего:

'rows' – Вход является матрицей подсчетов слов со строками, соответствующими документам.
'columns' – Вход является транспонированной матрицей подсчетов слов со столбцами, соответствующими документам.

Эта опция только применяется, если вы задаете входные документы как матрицу подсчетов слов.

Примечание

Если вы ориентируете свою матрицу для подсчета количества слов так, чтобы документы соответствовали столбцам и задали 'DocumentsIn','columns', затем вы можете испытать значительное сокращение во время выполнения оптимизации.

Пакетные опции решателя

свернуть все

`'IterationLimit'` — Максимальное количество итераций
100 (значение по умолчанию) | положительное целое число

Максимальное количество итераций в виде разделенной запятой пары, состоящей из 'IterationLimit' и положительное целое число.

Эта опция поддерживает пакетные решатели только ('cgs', 'avb', или 'cvb0').

Пример: 'IterationLimit',200

Стохастические опции решателя

свернуть все

`'DataPassLimit'` — Максимальное количество проходит через данные
1 (значение по умолчанию) | положительное целое число

Максимальное количество проходов через данные в виде разделенной запятой пары, состоящей из 'DataPassLimit' и положительное целое число.

Если вы задаете 'DataPassLimit' но не 'MiniBatchLimit', затем значение по умолчанию 'MiniBatchLimit' проигнорирован. Если вы задаете оба 'DataPassLimit' и 'MiniBatchLimit', затем fitlda использует аргумент, который приводит к обработке наименьшего количества наблюдений.

Эта опция поддерживает только стохастическое ('savb') решатель.

Пример: 'DataPassLimit',2

`'MiniBatchLimit'` — Максимальное количество мини-пакетных передач
положительное целое число

Максимальное количество мини-пакетных передач в виде разделенной запятой пары, состоящей из 'MiniBatchLimit' и положительное целое число.

Если вы задаете 'MiniBatchLimit' но не 'DataPassLimit', затем fitlda игнорирует значение по умолчанию 'DataPassLimit'. Если вы задаете оба 'MiniBatchLimit' и 'DataPassLimit', затем fitlda использует аргумент, который приводит к обработке наименьшего количества наблюдений. Значением по умолчанию является ceil(numDocuments/MiniBatchSize), где numDocuments количество входных документов.

Эта опция поддерживает только стохастическое ('savb') решатель.

Пример: 'MiniBatchLimit',200

`'MiniBatchSize'` — Мини-пакетный размер
1 000 (значений по умолчанию) | положительное целое число

Мини-пакетный размер в виде разделенной запятой пары, состоящей из 'MiniBatchLimit' и положительное целое число. Функциональные процессы MiniBatchSize документы в каждой итерации.

Эта опция поддерживает только стохастическое ('savb') решатель.

Пример: 'MiniBatchSize',512

`'LearnRateDecay'` — Затухание скорости обучения
0.5 (значение по умолчанию) | положительная скалярная величина, меньше чем или равная 1

Затухание скорости обучения в виде разделенной запятой пары 'LearnRateDecay' и положительная скалярная величина, меньше чем или равная 1.

Для мини-пакетного t функция устанавливает скорость обучения на $η (t) = 1 / {(1 + t)}^{κ}$ , где $κ$ затухание скорости обучения.

Если LearnRateDecay близко к 1, затем скорость обучения затухает быстрее, и модель извлекает уроки в основном из более ранних мини-пакетов. Если LearnRateDecay близко к 0, затем скорость обучения затухает медленнее, и модель продолжает извлекать уроки из большего количества мини-пакетов. Для получения дополнительной информации смотрите Стохастический Решатель.

Эта опция поддерживает стохастический решатель только ('savb').

Пример: 'LearnRateDecay',0.75

Параметры экрана

свернуть все

`'ValidationData'` — Данные о валидации
`[]` (значение по умолчанию) | `bagOfWords` возразите | `bagOfNgrams` возразите | разреженная матрица подсчетов слов

Данные о валидации, чтобы контролировать сходимость оптимизации в виде разделенной запятой пары, состоящей из 'ValidationData' и bagOfWords объект, bagOfNgrams объект или разреженная матрица подсчетов слов. Если данные о валидации являются матрицей, то данные должны иметь ту же ориентацию и то же количество слов как входные документы.

`'ValidationFrequency'` — Частота проверки допустимости модели
положительное целое число

Частота проверки допустимости модели в количестве итераций в виде разделенной запятой пары, состоящей из 'ValidationFrequency' и положительное целое число.

Значение по умолчанию зависит от решателя, используемого, чтобы подбирать модель. Для стохастического решателя значение по умолчанию равняется 10. Для других решателей значение по умолчанию равняется 1.

`'Verbose'` — Уровень многословия
1 (значение по умолчанию) | 0

Уровень многословия в виде разделенной запятой пары, состоящей из 'Verbose' и одно из следующего:

0 – Не отображайте многословный вывод.
1 – Отобразите информацию о прогрессе.

Пример: 'Verbose',0

Выходные аргументы

свернуть все

`mdl` — Модель Output LDA
`ldaModel` объект

Выведите модель LDA, возвращенную как ldaModel объект.

Больше о

свернуть все

Скрытое выделение Дирихле

Модель скрытого выделения Дирихле (LDA) является моделью тематики документа, которая обнаруживает базовые темы в наборе документов и выводит вероятности слова в темах. LDA моделирует набор документов D как смеси темы $θ_{1}, \dots, θ_{D}$ , по темам K, охарактеризованным векторами вероятностей слова $φ_{1}, \dots, φ_{K}$ . В модели принимается, что смеси темы $θ_{1}, \dots, θ_{D}$ , и темы $φ_{1}, \dots, φ_{K}$ следуйте за распределением Дирихле параметрами концентрации $α$ и $β$ соответственно.

Смеси темы $θ_{1}, \dots, θ_{D}$ векторы вероятности длины K, где K является количеством тем. Запись $θ_{d i}$ вероятность темы i, появляющийся в d th документ. Смеси темы соответствуют строкам DocumentTopicProbabilities свойство ldaModel объект.

Темы $φ_{1}, \dots, φ_{K}$ векторы вероятности длины V, где V является количеством слов в словаре. Запись $φ_{i v}$ соответствует вероятности v th слово словаря, появляющегося в i th тема. Темы $φ_{1}, \dots, φ_{K}$ соответствуйте столбцам TopicWordProbabilities свойство ldaModel объект.

Учитывая темы $φ_{1}, \dots, φ_{K}$ и предшествующий Дирихле $α$ на смесях темы LDA принимает следующий порождающий процесс для документа:

Произведите смесь темы $θ ~ Dirichlet (α)$ . Случайная переменная $θ$ вектор вероятности длины K, где K является количеством тем.
Для каждого слова в документе:
1. Произведите список тем $z ~ Categorical (θ)$ . z случайной переменной является целым числом от 1 до K, где K является количеством тем.
2. Произведите слово $w ~ Categorical (φ_{z})$ . w случайной переменной является целым числом от 1 до V, где V является количеством слов в словаре и представляет соответствующее слово в словаре.

При этом порождающем процессе, совместном распределении документа со словами $w_{1}, \dots, w_{N}$ , со смесью темы $θ$ , и с индексами темы $z_{1}, \dots, z_{N}$ дают

$p (θ, z, w | α, φ) = p (θ | α) \prod_{n = 1}^{N} p (z_{n} | θ) p (w_{n} | z_{n}, φ),$

где N является количеством слов в документе. Подведение итогов совместного распределения по z и затем интеграция $θ$ дает к предельному распределению документа w:

$p (w | α, φ) = \int_{θ} p (θ | α) \prod_{n = 1}^{N} \sum_{z_{n}} p (z_{n} | θ) p (w_{n} | z_{n}, φ) d θ .$

Следующая схема иллюстрирует модель LDA как вероятностную графическую модель. Теневые узлы являются наблюдаемыми переменными, незаштрихованные узлы являются скрытыми переменными, узлы без основ являются параметрами модели. Стрелы подсвечивают, что зависимости между случайными переменными и пластинами указывают на повторенные узлы.

Распределение Дирихле

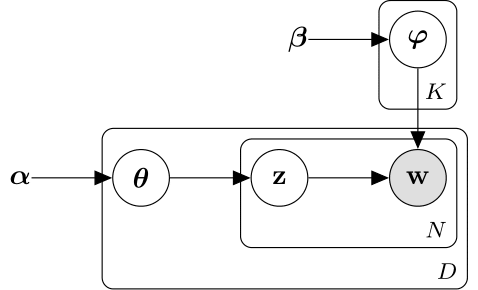
Распределение Дирихле является непрерывным обобщением распределения многочлена. Учитывая количество категорий $K \geq 2$ , и параметр концентрации $α$ , где $α$ вектор положительных реалов длины K, функцией плотности вероятности распределения Дирихле дают

$p (θ ∣ α) = \frac{1}{B (α)} \prod_{i = 1}^{K} θ_{i}^{α_{i} - 1},$

где B обозначает многомерную Бета-функцию, данную

$B (α) = \frac{\prod_{i = 1}^{K} Γ (α_{i})}{Γ (\sum_{i = 1}^{K} α_{i})} .$

Особый случай распределения Дирихле является симметричным распределением Дирихле. Симметричное распределение Дирихле характеризуется параметром концентрации $α$ , где все элементы $α$ то же самое.

Стохастический решатель

Стохастические документы процессов решателя в мини-пакетах. Это обновляет вероятности слова на тему с помощью взвешенной суммы вероятностей, вычисленных от каждого мини-пакета и вероятностей от всех предыдущих мини-пакетов.

Для мини-пакетного t решатель устанавливает скорость обучения на $η (t) = 1 / {(1 + t)}^{κ}$ , где $κ$ затухание скорости обучения.

Функция использует затухание скорости обучения, чтобы обновиться $Φ$ , матрица вероятностей слова на тему, путем установки

$Φ^{(t)} = (1 - η (t)) Φ^{(t - 1)} + η (t) Φ^{(t *)},$

где $Φ^{(t *)}$ матрица, усвоенная из мини-пакетного t, и $Φ^{(t - 1)}$ матрица, усвоенная из мини-пакетов 1 через t-1.

Прежде чем изучение начинается (когда t = 0), функция инициализирует начальные вероятности слова на тему со случайными значениями.

Вопросы совместимости

развернуть все

`fitlda` темы видов

Поведение изменяется в R2018b

Начиная в R2018b, fitlda, по умолчанию, сортирует темы в порядке убывания вероятностей темы входного набора документа. Это поведение облегчает находить темы с самыми высокими вероятностями.

В предыдущих версиях, fitlda не изменяет порядок темы. Чтобы воспроизвести поведение, установите 'TopicOrder' опция к 'unordered'.

Ссылки

[1] Foulds, Джеймс, Леви Бойлес, Кристофер Дюбуа, Padhraic Smyth и Макс Веллинг. "Стохастический свернутый вариационный Байесов вывод для скрытого выделения Дирихле". В Продолжениях 19-й международной конференции ACM SIGKDD по вопросам открытия Знаний и анализа данных, стр 446–454. ACM, 2013.

[2] Хоффман, Мэтью Д., Дэвид М. Блеи, Чон Ван и Джон Пэйсли. "Стохастический вариационный вывод". Журнал Исследования Машинного обучения 14, № 1 (2013): 1303–1347.

[3] Гриффитс, Томас Л. и Марк Стеиверс. "Находя научные темы". Продолжения Национальной академии наук 101, нет. suppl 1 (2004): 5228–5235.

[4] Асунсьон, Артур, Макс Веллинг, Padhraic Smyth и Yee Whye Teh. "При сглаживании и выводе для моделей темы". В Продолжениях Двадцать пятой Конференции по Неопределенности в Искусственном интеллекте, стр 27–34. Нажатие AUAI, 2009.

[5] Teh, Ии В., Дэвид Ньюман и Макс Веллинг. "Свернутый вариационный Байесов алгоритм вывода для скрытого выделения Дирихле". В Усовершенствованиях в нейронных системах обработки информации, стр 1353–1360. 2007.

Документация

fitlda

Синтаксис

Описание

Примеры

Подбирайте модель LDA

Подбирайте модель LDA к матрице для подсчета количества слов

Предскажите главные темы LDA документов

Входные параметры

bag — Модель Input bagOfWords возразите | bagOfNgrams объект

numTopics — Количество тем положительное целое число

counts — Подсчет частот слов матрица неотрицательных целых чисел

Аргументы в виде пар имя-значение

Опции решателя

'Solver' — Решатель для оптимизации 'cgs' (значение по умолчанию) | 'savb' | 'avb' | 'cvb0'

'LogLikelihoodTolerance' — Относительный допуск на логарифмической правдоподобности0.0001 (значение по умолчанию) | положительная скалярная величина

'FitTopicProbabilities' — Опция для подходящих корпусных вероятностей темы true (значение по умолчанию) | false

'FitTopicConcentration' — Опция для подходящей концентрации темы true | false

'InitialTopicConcentration' — Первоначальная оценка концентрации темы numTopics/4 (значение по умолчанию) | неотрицательный скаляр

'TopicOrder' — Порядок темы 'initial-fit-probability' (значение по умолчанию) | 'unordered'

'WordConcentration' — Концентрация Word1 (значение по умолчанию) | неотрицательный скаляр

'DocumentsIn' — Ориентация документов 'rows' (значение по умолчанию) | 'columns'

Примечание

Пакетные опции решателя

'IterationLimit' — Максимальное количество итераций100 (значение по умолчанию) | положительное целое число

Стохастические опции решателя

'DataPassLimit' — Максимальное количество проходит через данные 1 (значение по умолчанию) | положительное целое число

'MiniBatchLimit' — Максимальное количество мини-пакетных передач положительное целое число

'MiniBatchSize' — Мини-пакетный размер 1 000 (значений по умолчанию) | положительное целое число

'LearnRateDecay' — Затухание скорости обучения 0.5 (значение по умолчанию) | положительная скалярная величина, меньше чем или равная 1

Параметры экрана

'ValidationData' — Данные о валидации [] (значение по умолчанию) | bagOfWords возразите | bagOfNgrams возразите | разреженная матрица подсчетов слов

'ValidationFrequency' — Частота проверки допустимости модели положительное целое число

'Verbose' — Уровень многословия 1 (значение по умолчанию) | 0

Выходные аргументы

mdl — Модель Output LDA ldaModel объект

Больше о

Скрытое выделение Дирихле

Распределение Дирихле

Стохастический решатель

Вопросы совместимости

fitlda темы видов

Ссылки

Смотрите также

Темы

Введенный в R2017b

Документация Text Analytics Toolbox

Поддержка

`bag` — Модель Input
`bagOfWords` возразите | `bagOfNgrams` объект

`numTopics` — Количество тем
положительное целое число

`counts` — Подсчет частот слов
матрица неотрицательных целых чисел

`'Solver'` — Решатель для оптимизации
`'cgs'` (значение по умолчанию) | `'savb'` | `'avb'` | `'cvb0'`

`'LogLikelihoodTolerance'` — Относительный допуск на логарифмической правдоподобности
0.0001 (значение по умолчанию) | положительная скалярная величина

`'FitTopicProbabilities'` — Опция для подходящих корпусных вероятностей темы
`true` (значение по умолчанию) | `false`

`'FitTopicConcentration'` — Опция для подходящей концентрации темы
`true` | `false`

`'InitialTopicConcentration'` — Первоначальная оценка концентрации темы
`numTopics/4` (значение по умолчанию) | неотрицательный скаляр

`'TopicOrder'` — Порядок темы
`'initial-fit-probability'` (значение по умолчанию) | `'unordered'`

`'WordConcentration'` — Концентрация Word
1 (значение по умолчанию) | неотрицательный скаляр

`'DocumentsIn'` — Ориентация документов
`'rows'` (значение по умолчанию) | `'columns'`

`'IterationLimit'` — Максимальное количество итераций
100 (значение по умолчанию) | положительное целое число

`'DataPassLimit'` — Максимальное количество проходит через данные
1 (значение по умолчанию) | положительное целое число

`'MiniBatchLimit'` — Максимальное количество мини-пакетных передач
положительное целое число

`'MiniBatchSize'` — Мини-пакетный размер
1 000 (значений по умолчанию) | положительное целое число

`'LearnRateDecay'` — Затухание скорости обучения
0.5 (значение по умолчанию) | положительная скалярная величина, меньше чем или равная 1

`'ValidationData'` — Данные о валидации
`[]` (значение по умолчанию) | `bagOfWords` возразите | `bagOfNgrams` возразите | разреженная матрица подсчетов слов

`'ValidationFrequency'` — Частота проверки допустимости модели
положительное целое число

`'Verbose'` — Уровень многословия
1 (значение по умолчанию) | 0

`mdl` — Модель Output LDA
`ldaModel` объект

`fitlda` темы видов