Пакет вейвлета мультисигнала 1-D преобразовывает
wpt = dwpt(X)X. Вход X вектор с действительным знаком, матрица или расписание. По умолчанию, fk18 вейвлет используется, и уровнем разложения является floor(log2(Ns)), где Ns является количеством выборок данных. Пакет вейвлета преобразовывает wpt 1 N массивом ячеек, где N = 2^floor(log2(Ns)).
[ также возвращает уровни преобразования узлов wpt,l,packetlevels] = dwpt(___)wpt использование любого из предыдущих синтаксисов.
[ также возвращает центральные частоты аппроксимированных полос пропускания в циклах на выборку с помощью любого из предыдущих синтаксисов.wpt,l,packetlevels,f] = dwpt(___)
[ также возвращает относительную энергию для пакетов вейвлета в wpt,l,packetlevels,f,re] = dwpt(___)wpt использование любого из предыдущих синтаксисов. Относительная энергия является пропорцией энергии, содержавшейся в каждом пакете вейвлета уровнем.
[___] = dwpt(___, задает аргументы пары "имя-значение" использования опций в дополнение к входным параметрам в предыдущих синтаксисах. Например, Name,Value)'Level',4 задает уровень разложения.
dwpt функция выполняет дискретный пакет вейвлета, преобразовывают, и производит sequency-упорядоченное пакетное дерево вейвлета. Сравните sequency-упорядоченный и нормальное (Палей) - упорядоченный деревья. масштабирующийся (lowpass) аналитический фильтр, и представляет вейвлет (highpass) аналитический фильтр. Метки в нижней части показывают раздел оси частоты [0, ½].
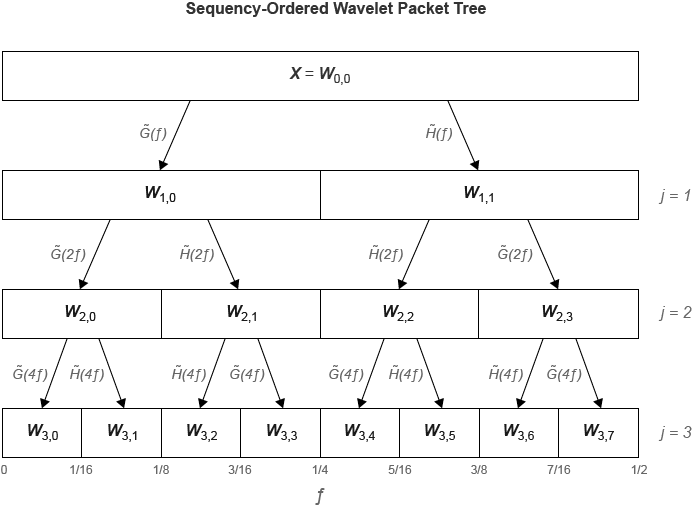
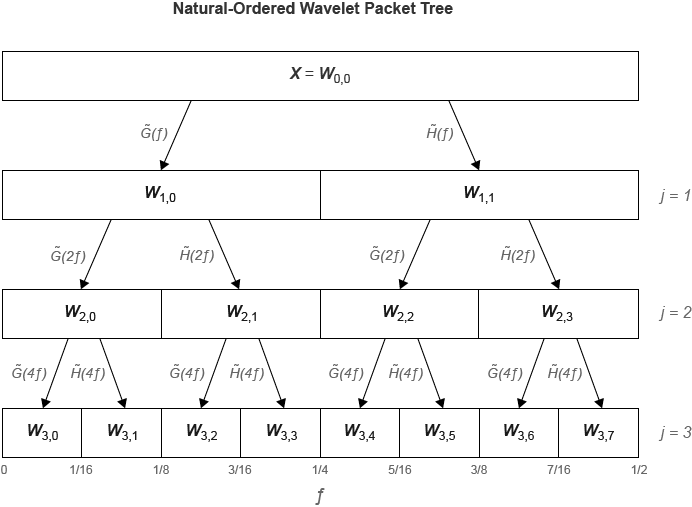
[1] Wickerhauser, Младен Виктор. Адаптированный анализ вейвлета от теории до программного обеспечения. Веллесли, MA: А.К. Питерс, 1994.
[2] Персиваль, D. B. и А. Т. Уолден. Методы вейвлета для анализа временных рядов. Кембридж, Великобритания: Издательство Кембриджского университета, 2000.
[3] Мезаструктура, Гектор. “Адаптированные Вейвлеты для Обнаружения Шаблона”. Происходящий в Распознавании образов, Анализе изображения и Приложениях, отредактированных Альберто Санфелиу и Мануелем Лазо Кортесом, 3773:933–44. Берлин, Гейдельберг: Спрингер Берлин Гейдельберг, 2005. https://doi.org/10.1007/11578079_96.