Максимальное перекрытие дискретный пакет вейвлета преобразовывает
wpt = modwpt(x)x.
Выход MODWPT задерживается временем по сравнению с входным сигналом. Большинство фильтров, используемых, чтобы получить MODWPT, имеет нелинейный фазовый отклик, который делает компенсацию задержки трудной. Это верно для всего ортогонального масштабирования и фильтров вейвлета, кроме вейвлета Хаара. Это возможно ко времени - выравнивают коэффициенты с функциями сигнала, но результатом является приближение, не точное выравнивание с исходным сигналом. Разделы MODWPT энергия среди пакетов вейвлета на каждом уровне. Сумма энергии по всем пакетам равняется полной энергии входного сигнала. Выход MODWPT полезен для приложений, где вы хотите анализировать энергетические уровни в различных пакетах.
Детали MODWPT (modwptdetails) результат фильтрации нулевой фазы сигнала. Функции в деталях MODWPT выравниваются точно с функциями во входном сигнале. Для данного уровня подведение итогов деталей для каждой выборки возвращает точный исходный сигнал. Выход деталей MODWPT полезен для приложений, которые требуют выравнивания времени, такого как непараметрический регрессионный анализ.
[ возвращает вектор уровней преобразования, соответствующих строкам wpt,packetlevs]
= modwpt(___)wpt.
[ возвращает центральные частоты аппроксимированных полос пропускания, соответствующих строкам wpt,packetlevs,cfreq]
= modwpt(___)wpt.
[ возвращается энергия (придал норме L2 квадратную форму) пакетных коэффициентов вейвлета для узлов в wpt,packetlevs,cfreq,energy]
= modwpt(___)wpt.
[___] = modwpt(___, возвращает MODWPT с дополнительными опциями, заданными одним или несколькими Name,Value)Name,Value парные аргументы.
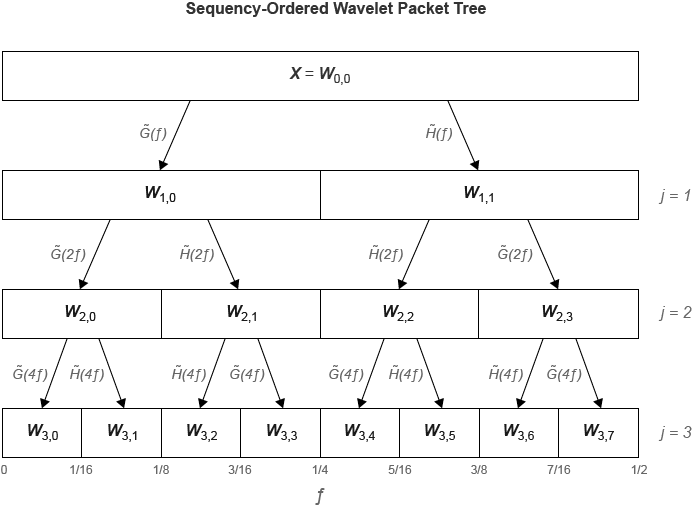
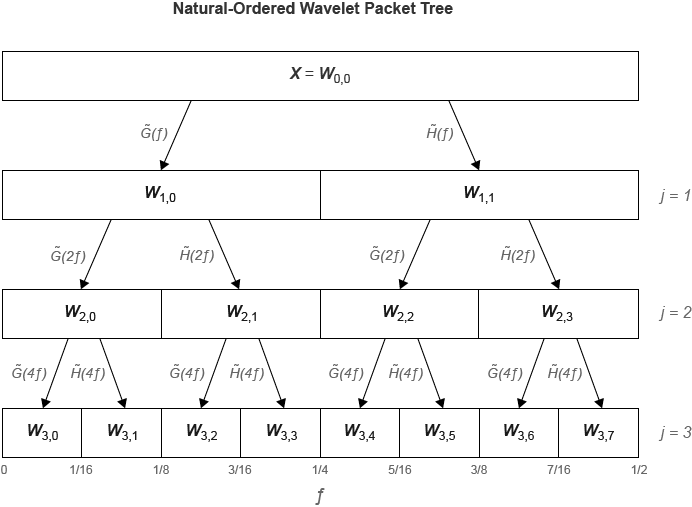
modwpt выполняет дискретный пакет вейвлета, преобразовывают, и производит sequency-упорядоченное пакетное дерево вейвлета. Сравните sequency-упорядоченный и нормальное (Палей) - упорядоченный деревья.
[1] Персиваль, D. B. и А. Т. Уолден. Методы вейвлета для анализа временных рядов. Кембридж, Великобритания: Издательство Кембриджского университета, 2000.
[2] Уолден, A.T., и А. Контрерас Кристан. “Откорректированный фазой неподкошенный дискретный пакет вейвлета преобразовывает и его приложение к интерпретации синхронизации событий”. Продолжения Королевского общества Лондона A. Издание 454, Выпуск 1976, 1998, стр 2243-2266.
dwpt | imodwpt | modwptdetails