Exponenta Banner

idwt

Одноуровневый обратный дискретный 1D вейвлет преобразовывает

свернуть все на странице

Синтаксис

X = idwt(cA,cD,'wname')
X = idwt(cA,cD,Lo_R,Hi_R)
X = idwt(cA,cD,'wname',L)
X = idwt(cA,cD,Lo_R,Hi_R,L)
idwt(cA,cD,'wname')
X = idwt(...,'mode',MODE)
X = idwt(cA,[],...)
X = idwt([],cD,...)

Описание

idwt команда выполняет одноуровневую одномерную реконструкцию вейвлета относительно любого конкретный вейвлет ('wname', смотрите wfilters для получения дополнительной информации) или конкретные фильтры реконструкции вейвлета (Lo_R и Hi_R) то, что вы задаете.

X = idwt(cA,cD,'wname') возвращает одноуровневый восстановленный содействующий вектор приближения X на основе приближения и содействующих векторов детали cA и cD, и использование вейвлета 'wname'.

X = idwt(cA,cD,Lo_R,Hi_R) восстанавливает как выше использования фильтров, которые вы задаете.

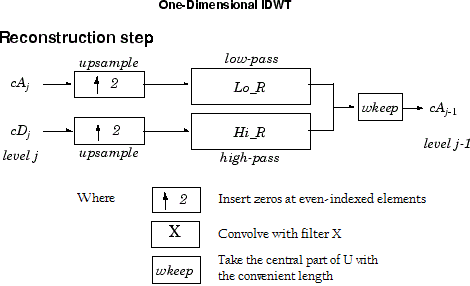
  • Lo_R реконструкция фильтр lowpass.

  • Hi_R фильтр высоких частот реконструкции.

Lo_R и Hi_R должна быть та же длина.

Позвольте la будьте длиной cA (который также равняется длине cD) и lf длина фильтров Lo_R и Hi_R; затем length(X) = LX где LX = 2*la если дополнительный режим DWT установлен в periodization. Для других дополнительных режимов LX = 2*la-lf+2.

Для получения дополнительной информации о различных Дискретных режимах расширения Преобразования Вейвлета, смотрите dwtmode.

X = idwt(cA,cD,'wname',L) или X = idwt(cA,cD,Lo_R,Hi_R,L) возвращает длину-L центральный фрагмент результата, полученного с помощью idwt(cA,cD,'wname')L должен быть меньше LX.

X = idwt(...,'mode',MODE) вычисляет реконструкцию вейвлета с помощью заданного дополнительного режима MODE.

X = idwt(cA,[],...) возвращает одноуровневый восстановленный содействующий вектор приближения X на основе содействующего вектора приближения cA.

X = idwt([],cD,...) возвращает одноуровневый восстановленный содействующий вектор детали X на основе содействующего вектора детали cD.

Примеры

свернуть все

Скрипт Open Live Script

Продемонстрируйте совершенную реконструкцию с помощью dwt и idwt с ортонормированным вейвлетом. 

load noisdopp;
[A,D] = dwt(noisdopp,'sym4');
x = idwt(A,D,'sym4');
max(abs(noisdopp-x))
ans = 3.2156e-12
Скрипт Open Live Script

Продемонстрируйте совершенную реконструкцию с помощью dwt и idwt с биоортогональным вейвлетом. 

load noisdopp;
[Lo_D,Hi_D,Lo_R,Hi_R] = wfilters('bior3.5');
[A,D] = dwt(noisdopp,Lo_D,Hi_D);
x = idwt(A,D,Lo_R,Hi_R);
max(abs(noisdopp-x))
ans = 3.5527e-15

Алгоритмы

Начинание с приближения и коэффициентов детали на уровне, который преобразовывают j, cA j и cDj, обратный дискретный вейвлет, восстанавливает cAj−1, инвертируя шаг разложения путем вставки нулей и свертки к результатам с фильтрами реконструкции.

Ссылки

Daubechies, я. (1992), Десять лекций по вейвлетам, ряду конференции CBMS-NSF в прикладной математике. SIAM Эд.

Mallat, S. (1989), “Теория для мультиразрешения сигнализирует о разложении: представление вейвлета”, Анальный Шаблон IEEE. и Машина Intell., издание 11, № 7, стр 674–693.

Мейер, Y. (1990), Ondelettes и opérateurs, Том 1, Герман Эд. (Английский перевод: Вейвлеты и операторы, Кембриджское Нажатие Унив. 1993.)

Расширенные возможности

Смотрите также

| |

Представлено до R2006a

Документация Wavelet Toolbox
Поддержка