Дискретный стационарный вейвлет преобразовывает 1D
SWC = swt(X,N,'wname')
SWC = swt(X,N,Lo_D,Hi_D)
[SWA,SWD] = swt(___)
swt выполняет многоуровневое 1D стационарное разложение вейвлета с помощью или ортогонального или биоортогонального вейвлета. Задайте вейвлет с помощью его имени ('wname', смотрите wfilters для получения дополнительной информации) или его фильтры разложения.
SWC = swt(X,N,' вычисляет стационарное разложение вейвлета wname')X сигнала на уровне N, использование 'wname'.
N должно быть строго положительное целое число (см. wmaxlev для получения дополнительной информации) и length(X) должен быть кратным 2 Н.
SWC = swt(X,N,Lo_D,Hi_D) вычисляет стационарное разложение вейвлета как выше, учитывая эти фильтры, как введено:
Lo_D разложение фильтр lowpass.
Hi_D фильтр высоких частот разложения.
Lo_D и Hi_D должна быть та же длина.
Выходная матрица SWC содержит векторы коэффициентов, сохраненных построчный:
Для 1 ≤ i ≤ N, выходная матрица SWC(i,:) содержит коэффициенты детали уровня i и SWC(N+1,:) содержит коэффициенты приближения уровня N.
[SWA,SWD] = swt(___) вычисляет приближения, SWA, и детали, SWD, стационарные коэффициенты вейвлета.
Векторы коэффициентов хранятся построчные:
Для 1 ≤ i ≤ N, выходная матрица SWA(i,:) содержит коэффициенты приближения уровня i и выходная матрица SWD(i,:) содержит коэффициенты детали уровня i.
swt задан с помощью периодического расширения. Продолжительность приближения и коэффициентов детали, вычисленных на каждом уровне, равняется длине сигнала.
Выполните многоуровневое стационарное разложение вейвлета сигнала.
Загрузите одномерный сигнал и получите его длину.
load noisbloc
s = noisbloc;
sLen = length(s);Выполните стационарное разложение вейвлета на уровне 3 сигнала с помощью 'db1'. Извлеките деталь и коэффициенты приближения на уровне 3.
[swa,swd] = swt(s,3,'db1');
swd3 = swd(3,:);
swa3 = swa(3,:);Постройте выход разложения.
plot(s)
xlim([0 sLen])
title('Original Signal')
Постройте приближение уровня 3 и детализируйте коэффициенты.
subplot(2,1,1) plot(swa3) xlim([0 sLen]) title('Level 3 Approximation coefficients') subplot(2,1,2) plot(swd3) xlim([0 sLen]) title('Level 3 Detail coefficients')
Учитывая s сигнала длины N, первый шаг SWT производит, начинающий с s, двух наборов коэффициентов: коэффициенты приближения cA1 и коэффициенты детали cD1. Эти векторы получены путем свертки к s с фильтром lowpass Lo_D для приближения, и с фильтром высоких частот Hi_D для детали.
Более точно первый шаг
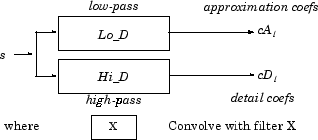
cA1 и cD1 имеют длину N вместо N/2 как в случае DWT.
Следующий шаг разделяет коэффициенты приближения cA1 в двух частях с помощью той же схемы, но с модифицированными фильтрами, полученными путем повышающей дискретизации фильтров, используемых в предыдущем шаге и заменяющий s cA1. Затем SWT производит cA2 и cD2. В более общем плане,
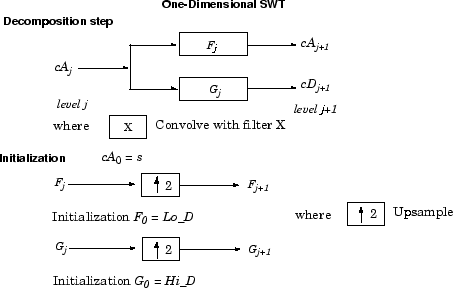
Нэзон, Г.П.; Б.В. Сильверман (1995), “Стационарный вейвлет преобразовывает и некоторые статистические приложения”, Примечания Лекции в Статистике, 103, стр 281–299.
Койфман, Р.Р.; Донохо, D.L. (1995), “Шумоподавление инварианта перевода”, Примечания Лекции в Статистике, 103, стр 125–150.
Pesquet, Дж.К.; Х. Крим, Х. Карфэйтан (1996), “Независимые от времени ортонормированные представления вейвлета”, Знак Сделки IEEE. Proc., издание 44, 8, стр 1964–1970.