wpfun

Пакетные функции вейвлета

Синтаксис

[WPWS,X] = wpfun('wname',NUM,PREC) [WPWS,X] = wpfun('wname',NUM) [WPWS,X] = wpfun('wname',NUM,7)

Описание

wpfun пакетная аналитическая функция вейвлета.

[WPWS,X] = wpfun('wname',NUM,PREC) вычисляет пакеты вейвлета для вейвлета 'wname' (см. wfilters для получения дополнительной информации), на двухместных интервалах длины ^2-PREC.

PREC должно быть положительное целое число. Выходная матрица WPWS содержит функции W индекса от 0 до NUM, сохраненный построчный как [_W0; _W1;...; W _NUM]. Выходной вектор X соответствующий общий X- вектор сетки.

[WPWS,X] = wpfun('wname',NUM) эквивалентно
[WPWS,X] = wpfun('wname',NUM,7).

Схема расчета пакетной генерации вейвлета легка при использовании ортогонального вейвлета. Мы начинаем с двух фильтров длины 2N, обозначил h (n) и g (n), соответствуя вейвлету.

Теперь индукцией позволяют нам задать следующую последовательность функций (_Wn (x) , n = 0,1,2...)

$\begin{array}{l} W_{2 n} (x) = \sqrt{2} \sum_{k = 0, \dots, 2 N - 1} h (k) W_{n} (2 x - k) \\ W_{2 n + 1} (x) = \sqrt{2} \sum_{k = 0, \dots, 2 N - 1} g (k) W_{n} (2 x - k) \end{array}$

где _W0 (x) = ϕ (x) является масштабирующейся функцией, и _W1 (x) = ψ (x) является функцией вейвлета.

Например, для вейвлета Хаара мы имеем

$N = 1, h (0) = h (1) = \frac{1}{\sqrt{2}}$

$g (0) = - g (1) = \frac{1}{\sqrt{2}}$

Уравнения становятся

$W_{2 n} (x) = W_{n} (2 x) + W_{n} (2 x - 1)$

$(W_{2 n + 1} (x) = W_{n} (2 x) - W_{n} (2 x - 1))$

_W0 (x) = ϕ (x) является haar масштабированием функции и _W1 (x) = ψ (x) является haar вейвлет, оба поддержанные в [0,1].

Затем мы можем получить _W2 _n путем добавления два 1/2-scaled версии _Wn с отличными поддержками [0,1/2] и [1/2,1] и получить _W2 _n ₊₁ путем вычитания тех же версий _Wn.

Начиная с более регулярных исходных вейвлетов, с помощью подобной конструкции, мы получаем сглаживавшие версии этой системы W - функции, все с поддержкой в интервале [0, 2N-1].

Примеры

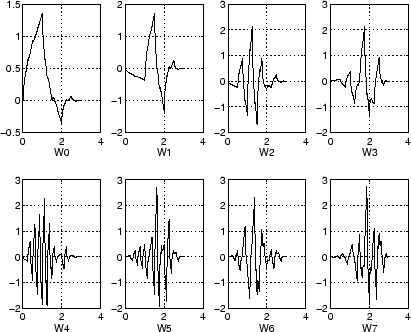
% Compute the db2 Wn functions for n = 0 to 7, generating 
% the db2 wavelet packets. 
[wp,x] = wpfun('db2',7);

% Using some plotting commands,
% the following figure is generated.

Ссылки

Койфман, R.R.; т-х Викераузер (1992), “Основанные на энтропии Алгоритмы для лучшего базисного выбора”, Сделка IEEE на Inf. Теория, издание 38, 2, стр 713–718.

Мейер, Y. (1993), Les ondelettes. Algorithmes и приложения, Колин Эд., Париж, 2-й выпуск. (Английский перевод: Вейвлеты: Алгоритмы и приложения, SIAM).

Wickerhauser, Т-х (1991), “INRIA читает лекции по пакетным алгоритмам вейвлета”, Продолжения ondelettes и paquets d'ondes, 17-21 июня, Rocquencourt, Франция, стр 31–99.

Wickerhauser, Т-х (1994), Адаптированный анализ вейвлета от теории до алгоритмов программного обеспечения, А.К. Питерса.

Смотрите также

wavefun | waveinfo

Документация

wpfun

Синтаксис

Описание

Примеры

Ссылки

Смотрите также

Представлено до R2006a

Документация Wavelet Toolbox

Поддержка