Алгоритм Быстрого вейвлета преобразовывает (FWT)

В 1 988, Mallat произвел быстрый алгоритм разложения и реконструкции вейвлета [1]. Алгоритм Mallat для дискретного вейвлета преобразовывает (DWT) является, на самом деле, классической схемой в сообществе обработки сигналов, известном как двухканальный кодер поддиапазона, использующий сопряженные квадратурные фильтры или квадратурные фильтры зеркала (QMFs).

Алгоритм разложения запускается с s сигнала, затем вычисляет координаты A ₁ и D ₁, и затем те из A ₂ и D ₂, и так далее.
Алгоритм реконструкции, названный обратным дискретным вейвлетом преобразовывает (IDWT), начинает с координат _AJ и _DJ, затем вычисляет координаты _AJ _–1, и затем использование координат _AJ _–1 и _DJ _–1 вычисляет те _{из AJ} _–2 и так далее.

Этот раздел обращается к следующим темам:

Фильтры, используемые, чтобы вычислить DWT и IDWT

Для ортогонального вейвлета, в среде мультиразрешения, мы начинаем с масштабирующейся функции φ и функции вейвлета ψ. Одно из основных отношений является отношением двойной шкалы (уравнение расширения или уравнение улучшения):

$\frac{1}{2} ϕ (\frac{x}{2}) = \sum_{n \in Z} w_{n} ϕ (x - n)$

Все фильтры, используемые в DWT и IDWT, глубоко связаны с последовательностью

(_wn) _n∊Z

Очевидно, если φ сжато поддержан, последовательность (_wn) конечна и может быть просмотрена как фильтр. Фильтр W, который называется масштабирующимся (ненормированным) фильтром,

Конечная импульсная характеристика (FIR)
Из длины 2N
Из суммы 1
Из нормы $\frac{1}{\sqrt{2}}$
Из нормы 1
Фильтр lowpass

Например, для db3 масштабирование фильтра,

load db3 
db3
    db3 =
    0.2352   0.5706   0.3252  -0.0955  -0.0604   0.0249

sum(db3)
    ans =
         1.0000

norm(db3)
    ans =
         0.7071

От фильтра W мы задаем четыре КИХ-фильтра, длины 2N и нормы 1, организованный можно следующим образом.

Фильтры	Lowpass	Высокая передача
Разложение	Lo_D	Hi_D
Реконструкция	Lo_R	Hi_R

Четыре фильтра вычисляются с помощью следующей схемы.

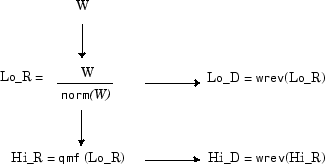
где qmf таково, что Hi_R и Lo_R являются квадратурными фильтрами зеркала (т.е. Hi_R (k) = (–1) ^kLo_R (2N + 1 – k)) для k = 1, 2..., 2N.

Обратите внимание на то, что wrev инвертирует коэффициенты фильтра. Таким образом, Hi_D и Lo_D являются также квадратурными фильтрами зеркала. Расчет этих фильтров выполняется с помощью orthfilt. Затем мы иллюстрируем эти свойства с db6 вейвлет.

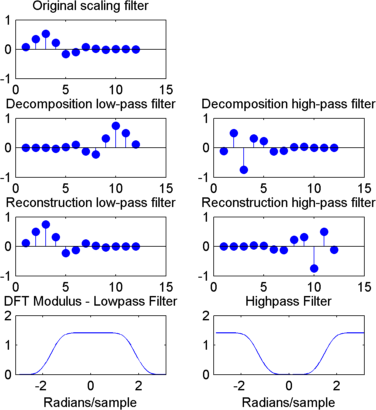
Загрузите экстремальный фильтр масштабирования фазы Добечиса и постройте коэффициенты.

load db6;
subplot(421); stem(db6,'markerfacecolor',[0 0 1]);
title('Original scaling filter');

Используйте orthfilt возвратить анализ (разложение) и синтез (реконструкция) фильтры.

Получите дискретные преобразования Фурье (DFT) lowpass и highpass аналитических фильтров. Постройте модуль ДПФ.

LoDFT = fft(Lo_D,64);
HiDFT = fft(Hi_D,64);
freq = -pi+(2*pi)/64:(2*pi)/64:pi;
subplot(427); plot(freq,fftshift(abs(LoDFT)));
set(gca,'xlim',[-pi,pi]); xlabel('Radians/sample');
title('DFT Modulus - Lowpass Filter')
subplot(428); plot(freq,fftshift(abs(HiDFT)));
set(gca,'xlim',[-pi,pi]); xlabel('Radians/sample');
title('Highpass Filter');

Алгоритмы

Учитывая s сигнала длины N, DWT состоит из этапов _log2N самое большее. Начиная с s, первый шаг производит два набора коэффициентов: коэффициенты приближения cA ₁ и коэффициенты детали cD ₁. Эти векторы получены путем свертки к s с Lo_D фильтра lowpass для приближения, и с фильтром высоких частот Hi_D для детали, сопровождаемой двухместной децимацией.

Более точно первый шаг

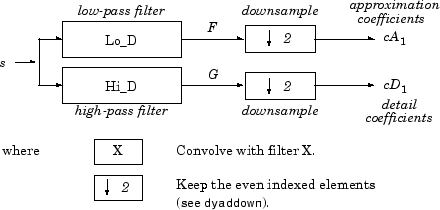
Длина каждого фильтра равна 2L. Результатом свертки к длине сигнал N с длиной 2L фильтр является N +2L–1. Поэтому сигналы F и G имеют длину N + 2L – 1. После субдискретизации 2, векторы коэффициентов cA ₁ и cD ₁ имеет длину

$⌊ \frac{N - 1}{2} + L ⌋ .$

Следующий шаг разделяет коэффициенты приближения cA ₁ в двух частях с помощью той же схемы, заменяя s cA ₁ и производя cA ₂ и cD ₂, и так далее.

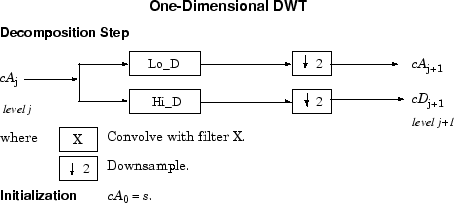
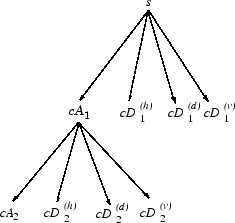
Так разложение вейвлета s сигнала, анализируемого на уровне, j имеет следующую структуру: [_cAj, _cDj..., cD ₁].

Эта структура содержит для J = 3 терминальные узлы следующего дерева.

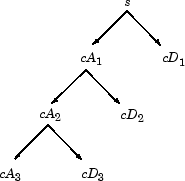
С другой стороны, запуская с cA _j и cD _j, IDWT восстанавливает cA _{j –1}, инвертируя шаг разложения путем вставки нулей и свертки к результатам с фильтрами реконструкции.
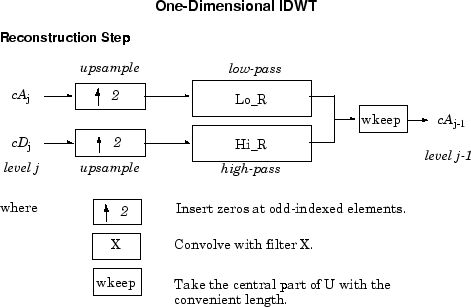
Для изображений подобный алгоритм возможен для двумерных вейвлетов и масштабирующихся функций, полученных из 1D вейвлетов tensorial продуктом.
Этот вид 2D DWT приводит к разложению коэффициентов приближения на уровне j в четырех компонентах: приближение на уровне j + 1 и детали в трех ориентациях (горизонталь, вертикальная, и диагональная).
Следующие графики описывают основные шаги разложения и реконструкции для изображений.

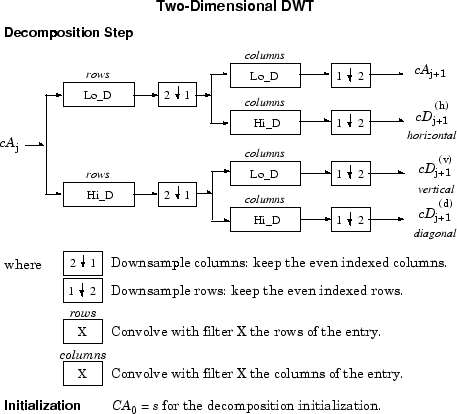
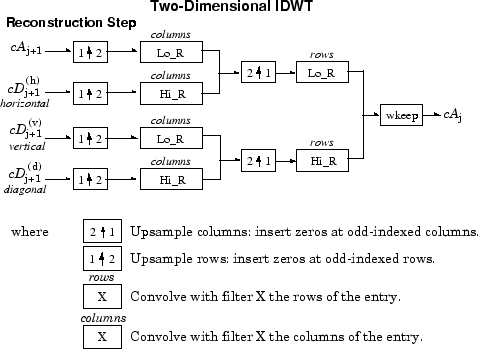
Так, для J = 2, 2D дерево вейвлета имеет следующую форму.

Наконец, давайте упомянем, что для биоортогональных вейвлетов те же алгоритмы содержат, но фильтры разложения с одной стороны и фильтры реконструкции, с другой стороны, получены из двух отличных функций масштабирования, сопоставленных с двумя исследованиями мультиразрешения в дуальности.

В этом случае фильтры для разложения и реконструкции, в целом, различных нечетных длин. Эта ситуация происходит, например, для “сплайнов” биоортогональные вейвлеты, используемые в тулбоксе. Дополнением нуля четыре фильтра могут быть расширены таким способом, которым у них будет та же ровная длина.

Почему такой алгоритм существует?

Предыдущий абзац описывает алгоритмы, спроектированные для сигналов конечной длины или изображений. Чтобы изучить объяснение, мы должны рассмотреть сигналы бесконечной длины. Методы для расширения данного сигнала конечной длины описаны в Краевых эффектах.

Давайте обозначим h = Lo_R и g = Hi_R и давайте фокусироваться на 1D случае.

Мы сначала выравниваем по ширине, как пойти от уровня j, чтобы выровнять j +1 для вектора приближения. Это - основной шаг алгоритма разложения для расчета приближений. Детали вычисляются таким же образом с помощью фильтра g вместо фильтра h.

Позвольте (_Ak ^(j)) k ∊Z быть координатами векторного _Aj:

$A_{j} = \sum_{k} A_{k}^{(j)} ϕ_{j, k}$

и _Ak ^{(j +1)} координаты векторного _Aj ₊₁:

$A_{j + 1} = \sum_{k} A_{k}^{(j + 1)} ϕ_{j + 1, k}$

_Ak ^{(j +1)} вычисляется с помощью формулы

$A_{k}^{(j + 1)} = \sum_{n} h_{n - 2 k} A_{n}^{(j)}$

Эта формула напоминает формулу свертки.

Расчет очень прост.

Давайте зададим

$\tilde{h} (k) = h (- k), и F_{k}^{(j + 1)} = \sum_{n} {\tilde{h}}_{k - n} A n^{(j)} .$

Последовательностью F ^{(j +1)} является отфильтрованный выход последовательности A ^(j) фильтром $\tilde{h}$ .

Мы получаем

_Ak ^{(j +1)} = F _2k ^{(j +1)}

Мы должны принять даже значения индекса F. Это прореживает.

Последовательность A ^{(j +1)} является прореженной версией последовательности F ^{(j +1)}.

Инициализация выполняется с помощью _Ak ⁽⁰⁾ = s (k), где s (k) является значением сигналов во время k.

Существует несколько причин этого неожиданного результата, все из которых соединяются с ситуацией с мультиразрешением и с несколькими свойств функций φ_j,k и ψ_j,k.

Давайте теперь опишем некоторых из них.

Семейство $(ϕ_{0, k}, k \in Z)$ формируется из ортонормированных функций. Как следствие для любого j, семейства $(ϕ_{j, k}, k \in Z)$ ортонормировано.
Двойное индексируемое семейство

$(ψ_{j, k}, j \in Z, k \in Z)$
ортонормировано.
Для любого j, $(ϕ_{j, k}, k \in Z)$ являются ортогональными к $(ψ_{j^{'}, k}, j^{'} \leq j, k \in Z)$ .
Между двумя последовательными шкалами у нас есть основное отношение, названное отношением двойной шкалы.

Отношение двойной шкалы для $ϕ$

$ϕ_{1, 0} = \sum_{k \in Z} h_{k} ϕ_{0, k}$

$ϕ_{j + 1, 0} = \sum_{k \in Z} h_{k} ϕ_{j, k}$

Это отношение вводит фильтр h алгоритма $(h_{n} = \sqrt{2 ω_{n}})$ . Для получения дополнительной информации смотрите Фильтры, Используемые, чтобы Вычислить DWT и IDWT.
Мы проверяем что:
1. Координата _φj+1,0 на _{φj,k is}_hk и не зависит от j.
2. Координата _{φj+1, n} на φ_j,k равен $〈 ϕ_{j + 1, n}, ϕ_{j, k} 〉 = h_{k - 2 n}$ .
Эти отношения предоставляют ингредиенты для алгоритма.
До сих пор мы использовали фильтр h. Фильтр высоких частот g используется в двойном отношении шкал, соединяющем функции φ и ψ. Между двумя последовательными шкалами у нас есть следующее фундаментальное отношение двойной шкалы.

Отношение двойной шкалы между $ψ$ и $ϕ$

$ψ_{1, 0} = \sum_{k \in Z} g_{k} ϕ_{0, k}$

$ψ_{j + 1, 0} = \sum_{k \in Z} g_{k} ϕ_{j, k}$
После шага разложения мы выравниваем по ширине теперь алгоритм реконструкции путем создания его. Давайте упростим обозначение. При запуске с A ₁ и D ₁, давайте изучим A ₀ = A ₁ + _Dj ₁. Процедура является тем же самым, чтобы вычислить A = _Aj ₊₁ + _Dj ₊₁.
Давайте зададим α_n, δ_n, $α_{k}^{0}$
$A_{1} = \sum_{n} a_{n} ϕ_{1, n} D_{1} = \sum_{n} δ_{n} ψ_{1, n} A_{0} = \sum_{k} a_{k}^{0} ϕ_{0, k}$
Давайте оценим $α_{k}^{0}$ координаты как
$\begin{array}{l} a_{k}^{0} = 〈 A_{0}, ϕ_{0, k} 〉 = 〈 A_{1} + D_{1}, ϕ_{0, k} 〉 = 〈 A_{1}, ϕ_{0, k} 〉 + 〈 D_{1}, ϕ_{0, k} 〉 \\ = \sum_{n} a_{n} 〈 ϕ_{1, n}, ϕ_{0, k} 〉 + \sum_{n} δ_{n} 〈 ψ_{1, n}, ϕ_{0, k} 〉 \\ = \sum_{n} a_{n} h_{k - 2 n} + \sum_{n} δ_{n} g_{k - 2 n} \end{array}$

Отношение двойной шкалы для $ϕ$
$ϕ_{1, 0} = \sum_{k \in Z} h_{k} ϕ_{0, k}$	$ϕ_{j + 1, 0} = \sum_{k \in Z} h_{k} ϕ_{j, k}$

Отношение двойной шкалы между $ψ$ и $ϕ$
$ψ_{1, 0} = \sum_{k \in Z} g_{k} ϕ_{0, k}$	$ψ_{j + 1, 0} = \sum_{k \in Z} g_{k} ϕ_{j, k}$

Мы будем фокусировать наше исследование первой суммы $\sum_{n} a_{n} h_{k - 2 n};$ вторая сумма $\sum_{n} δ_{n} g_{k - 2 n}$ обработан подобным образом.

Вычисления легко организованы, если мы отмечаем, что (взятие k = 0 в предыдущих формулах, делает вещи более простыми),

$\begin{array}{l} \sum_{n} a_{n} h_{- 2 n} = \dots + a_{- 1} h_{2} + a_{0} h_{0} + a_{1} h_{- 2} + a_{2} h_{- 4} + \dots \\ = \dots + a_{- 1} h_{2} + 0 h_{1} + a_{0} h_{0} + 0 h_{- 1} + a_{1} h_{- 2} + 0 h_{- 3} + a_{2} h_{- 4} + \dots \end{array}$

Если мы преобразовываем $(α_{n})$ последовательность в новую последовательность $({\tilde{α}}_{n})$ заданный

..., _α–1, 0, _α0, 0, _α1, 0, _α2, 0... который является точно

${\tilde{a}}_{2 n} = a_{n}, {\tilde{a}}_{2 n} + 1 = 0$

Затем

$\sum_{n} a_{n} h_{- 2 n} = \sum_{n} {\tilde{a}}_{n} h_{- n}$

и следовательно

$\sum_{n} a_{n} h_{k - 2 n} = \sum_{n} {\tilde{a}}_{n} h_{k - n}$

С тех пор

$a_{k}^{0} = \sum_{n} {\tilde{a}}_{n} h_{k - n} + \sum_{n} {\tilde{δ}}_{n} g_{k - n}$

шаги реконструкции:

Замените α и δ последовательности сверхдискретизированными версиями α ˜ и $\tilde{δ}$ вставка нулей.
Фильтр по h и g соответственно.
Суммируйте полученные последовательности.

1D возможности вейвлета

Основные 1D объекты

	Объекты	Описание
Сигнал в исходное время	s _Ak, 0 ≤ k ≤ j _Dk, 1 ≤ k ≤ j	Исходный сигнал Приближение на уровне k Детализируйте на уровне k
Коэффициенты в связанное со шкалой время	_cAk, 1 ≤ k ≤ j _cDk, 1 ≤ k ≤ j [_cAj, _cDj..., cD ₁]	Коэффициенты приближения на уровне k Детализируйте коэффициенты на уровне k Разложение вейвлета на уровне j, j ≥ 1

Объекты

Описание

Сигнал в исходное время

_Ak, 0 ≤ k ≤ j

_Dk, 1 ≤ k ≤ j

Исходный сигнал

Приближение на уровне k

Детализируйте на уровне k

Коэффициенты в связанное со шкалой время

_cAk, 1 ≤ k ≤ j

_cDk, 1 ≤ k ≤ j

[_cAj, _cDj..., cD ₁]

Коэффициенты приближения на уровне k

Детализируйте коэффициенты на уровне k

Разложение вейвлета на уровне j, j ≥ 1

Возможности аналитического разложения

Цель	Входной параметр	Вывод	Файл
Одноуровневое разложение	s	cA ₁, cD ₁	`dwt`
Одноуровневое разложение	_cAj	_cAj ₊₁, _cDj ₊₁	`dwt`
Разложение	s	[_cAj, _cDj..., cD ₁]	`wavedec`

Возможности реконструкции синтеза

Цель	Входной параметр	Вывод	Файл
Одноуровневая реконструкция	cA ₁, cD ₁	s или A ₀	`idwt`
Одноуровневая реконструкция	_cAj ₊₁, _cDj ₊₁	_cAj	`idwt`
Полная реконструкция	[_cAj, _cDj..., cD ₁]	s или A ₀	`waverec`
Выборочная реконструкция	[_cAj, _cDj..., cD ₁]	_Al, _Dm	`wrcoef`

Утилиты структуры разложения

Цель	Входной параметр	Вывод	Файл
Экстракция коэффициентов детали	[_cAj, _cDj..., cD ₁]	_cDk, 1 ≤ k ≤ j	`detcoef`
Экстракция коэффициентов приближения	[_cAj, _cDj..., cD ₁]	_cAk, 0 ≤ k ≤ j	`appcoef`
Пересостав структуры разложения	[_cAj, _cDj..., cD ₁]	[_cAk, _cDk..., cD ₁] 1 ≤ k ≤ j	`upwlev`

Чтобы проиллюстрировать режим командной строки для 1D возможностей, смотрите, что 1D Анализ Использует Командную строку..

2D возможности вейвлета

Основные 2D объекты

	Объекты	Описание
Отобразите в исходном разрешении	s	Оригинальное изображение
	A ₀	Приближение на уровне 0
	_Ak, 1 ≤ k ≤ j	Приближение на уровне k
	_Dk, 1 ≤ k ≤ j	Детали на уровне k
Коэффициенты в связанном со шкалой разрешении	_cAk, 1 ≤ k ≤ j	Коэффициенты приближения на уровне k
	_cDk, 1 ≤ k ≤ j	Детализируйте коэффициенты на уровне k
	[_cAj, _cDj..., cD ₁]	Разложение вейвлета на уровне j

_Dk обозначает $[D_{k}^{(h)}, D_{k}^{(v)}, D_{k}^{(d)}]$ , горизонталь, вертикальные, и диагональные детали на уровне k.

То же самое содержит для _cDk, который обозначает $[c D_{k}^{(h)}, c D_{k}^{(v)}, c D_{k}^{(d)}]$ .

2D файлы совпадают с теми для 1D случая, но с 2 добавленный на конце команды.

Например, idwt становится idwt2. Для получения дополнительной информации смотрите 1D Возможности Вейвлета.

Чтобы проиллюстрировать режим командной строки для 2D возможностей, смотрите Анализ изображения Вейвлета и Сжатие..

Ссылки

[1] Mallat, S. G. “Теория для Разложения Сигнала Мультиразрешения: Представление Вейвлета”, Транзакции IEEE согласно Анализу Шаблона и Искусственному интеллекту. Издание 11, Выпуск 7, июль 1989, стр 674–693.

Документация