Simple Variable Mass 6DOF (Euler Angles)

Реализуйте представление Угла Эйлера шести уравнений степеней свободы движения массы простой переменной

Библиотека:
Aerospace Blockset / уравнения Движения / 6DOF

Описание

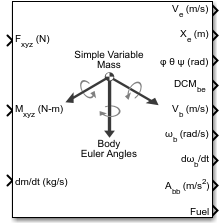
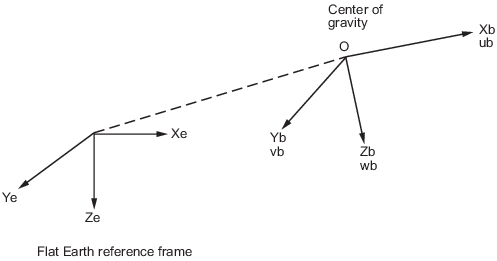
Блок Simple Variable Mass 6DOF (Euler Angles) рассматривает вращение зафиксированной телом координатной системы координат (_Xb, _Yb, _Zb) о плоской Наземной системе координат (_Xe, _Ye, _Ze).

Для описания системы координат и поступательной динамики, см. описание для блока Simple Variable Mass 6DOF (Euler Angles). Для получения дополнительной информации о зафиксированной телом координатной системе координат см. Алгоритмы.

Ограничения

Блок принимает, что приложенные силы действуют в центре тяжести тела.

Порты

Входной параметр

развернуть все

`_Fxyz` — Приложенные силы
трехэлементный вектор

Приложенные силы в виде трехэлементного вектора.

Типы данных: double

`_Mxyz(N-m)` — Прикладные моменты
трехэлементный вектор

Прикладные моменты в виде трехэлементного вектора.

Типы данных: double

`dm/dt (kg/s)` — Скорость изменения массы
скаляр

Одна или несколько скоростей изменения массы (положительный, если аккумулируется, отрицательный, если удалено) в виде скаляра.

Типы данных: double

`_Vre` — Относительная скорость
трехэлементный вектор

Одна или несколько относительных скоростей в виде трехэлементного вектора, в котором масса аккумулируется к или удаляется от тела в зафиксированных телом осях.

Зависимости

Чтобы включить этот порт, выберите Include mass flow relative velocity.

Типы данных: double

Вывод

развернуть все

`_Ve` — Скорость в плоской Наземной системе координат
трехэлементный вектор

Скорость в плоской Наземной системе координат, возвращенной как трехэлементный вектор.

Типы данных: double

`_Xe` — Положение в плоской Наземной системе координат
трехэлементный вектор

Положение в плоской Наземной системе координат, возвращенной как трехэлементный вектор.

Типы данных: double

`φ θ ψ (rad)` — Эйлеровы углы поворота
трехэлементный вектор

Эйлеровы углы поворота [список, подача, отклонение от курса], возвратились как трехэлементный вектор в радианах.

Типы данных: double

`_DCMbe` — Координатное преобразование
3х3 матрица

Координатное преобразование от плоских Наземных осей до зафиксированных телом осей, возвращенных как 3х3 матрица.

Типы данных: double

`_Vb` — Скорость в зафиксированной телом системе координат
трехэлементный вектор

Скорость в зафиксированной телом системе координат, возвращенной как трехэлементный вектор.

Типы данных: double

`_{ωb (rad/s)}` — Угловые уровни в зафиксированных телом осях
трехэлементный вектор

Угловые уровни в зафиксированных телом осях, возвращенных как трехэлементный вектор, в радианах в секунду.

Типы данных: double

`_dωb/dt` — Угловые ускорения
трехэлементный вектор

Угловые ускорения в зафиксированных телом осях, возвращенных как трехэлементный вектор, в радианах в секунду, придали квадратную форму.

Типы данных: double

`_Abb` — Ускорения в зафиксированных телом осях
трехэлементный вектор

Ускорения в зафиксированных телом осях относительно системы координат тела, возвращенной как трехэлементный вектор.

Типы данных: double

`Fuel` — Состояние топливного бака
скаляр

Состояние топливного бака, возвращенное как:

1 — Бак полон.
0 — Бак не полон и не пуст.
-1 — Бак пуст.

Типы данных: double

`_Abe` — Ускорения относительно инерционной системы координат
трехэлементный вектор

Ускорения в зафиксированных телом осях относительно инерционной системы координат (плоская Земля), возвращенный как трехэлементный вектор. Вы обычно соединяете этот сигнал с акселерометром.

Зависимости

Этот порт появляется только, когда флажок Include inertial acceleration устанавливается.

Типы данных: double

Параметры

развернуть все

Основной

`Units` — Модули ввода и вывода
`Metric (MKS)` (значение по умолчанию) | `English (Velocity in ft/s)` | `English (Velocity in kts)`

Модули ввода и вывода в виде Metric (MKS), English (Velocity in ft/s), или English (Velocity in kts).

Модули	Силы	Момент	Ускорение	Скорость	Положение	Масса	Инерция
`Metric (MKS)`	Ньютон	Ньютон-метр	Метры в секунду придали квадратную форму	Метры в секунду	Метры	Килограмм	Килограммометр придал квадратную форму
`English (Velocity in ft/s)`	Фунт	Футо-фунт	Ноги в секунду придали квадратную форму	Ноги в секунду	Футы	Краткий заголовок	Отложите нога придала квадратную форму
`English (Velocity in kts)`	Фунт	Футо-фунт	Ноги в секунду придали квадратную форму	Узлы	Футы	Краткий заголовок	Отложите нога придала квадратную форму

Программируемое использование

Параметры блоков: units

Ввод: символьный вектор

Значения: Metric (MKS) | English (Velocity in ft/s) | English (Velocity in kts)

Значение по умолчанию: Metric (MKS)

`Mass Type` — Массовый тип
`Simple Variable` (значение по умолчанию) | `Fixed` | `Custom Variable`

Массовый тип, заданный согласно следующей таблице.

Массовый тип	Описание	Значение по умолчанию для
`Fixed`	Масса является постоянной в течение симуляции.	6DOF (Euler Angles) 6DOF (Quaternion) 6DOF Wind (Wind Angles) 6DOF Wind (Quaternion) 6DOF ECEF (Quaternion)
`Simple Variable`	Масса и инерция варьируются линейно как функция массового уровня.	Simple Variable Mass 6DOF (Euler Angles) Simple Variable Mass 6DOF (Quaternion) Simple Variable Mass 6DOF Wind (Wind Angles) Simple Variable Mass 6DOF Wind (Quaternion) Simple Variable Mass 6DOF ECEF (Quaternion)
`Custom Variable`	Масса и изменения инерции настраиваемы.	Custom Variable Mass 6DOF (Euler Angles) Custom Variable Mass 6DOF (Quaternion) Custom Variable Mass 6DOF Wind (Wind Angles) Custom Variable Mass 6DOF Wind (Quaternion) Custom Variable Mass 6DOF ECEF (Quaternion)

Simple Variable выбор соответствует уравнениям движения в Алгоритмах.

Программируемое использование

Параметры блоков: mtype

Ввод: символьный вектор

Значения: Fixed | Simple Variable | Custom Variable

Значение по умолчанию: Simple Variable

`Representation` — Уравнения представления движения
`Euler Angles` (значение по умолчанию) | `Quaternion`

Уравнения представления движения, заданного согласно следующей таблице.

Представление	Описание
`Euler Angles`	Используйте Углы Эйлера в рамках уравнений движения.
`Quaternion`	Используйте кватернионы в рамках уравнений движения.

Euler Angles выбор соответствует уравнениям движения в Алгоритмах.

Программируемое использование

Параметры блоков: rep

Ввод: символьный вектор

Значения: Euler Angles | Quaternion

Значение по умолчанию: 'Euler Angles'

`Initial position in inertial axes [Xe,Ye,Ze]` — Положение в инерционных осях
[0 0 0] (значение по умолчанию) | трехэлементный вектор

Начальное местоположение тела в плоской Наземной системе координат в виде трехэлементного вектора.

Программируемое использование

Параметры блоков: xme_0

Ввод: символьный вектор

Значения: '[0 0 0]' | трехэлементный вектор

Значение по умолчанию: '[0 0 0]'

`Initial velocity in body axes [U,v,w]` — Скорость в осях тела
[0 0 0] (значение по умолчанию) | трехэлементный вектор

Начальная скорость в осях тела в виде трехэлементного вектора, в зафиксированной телом координатной системе координат.

Программируемое использование

Параметры блоков: Vm_0

Ввод: символьный вектор

Значения: '[0 0 0]' | трехэлементный вектор

Значение по умолчанию: '[0 0 0]'

`Initial Euler orientation [roll, pitch, yaw]` — Начальная Эйлерова ориентация
[0 0 0] (значение по умолчанию) | трехэлементный вектор

Начальные Эйлеровы углы ориентации [список, подача, отклонение от курса] в виде трехэлементного вектора, в радианах. Эйлеровы углы поворота - те между телом и северо-востоком вниз (NED) системы координат.

Программируемое использование

Параметры блоков: eul_0

Ввод: символьный вектор

Значения: '[0 0 0]' | трехэлементный вектор

Значение по умолчанию: '[0 0 0]'

`Initial body rotation rates [p,q,r]` — Начальное вращение тела
[0 0 0] (значение по умолчанию) | трехэлементный вектор

Начальная буква зафиксированные телом угловые уровни относительно NED структурирует в виде трехэлементного вектора в радианах в секунду.

Программируемое использование

Параметры блоков: pm_0

Ввод: символьный вектор

Значения: '[0 0 0]' | трехэлементный вектор

Значение по умолчанию: '[0 0 0]'

`Initial mass` — Начальная масса
1.0 (значение по умолчанию) | скаляр

Начальная масса твердого тела в виде двойного скаляра.

Программируемое использование

Параметры блоков: mass_0

Ввод: символьный вектор

Значения: '1.0' | двойной скаляр

Значение по умолчанию: '1.0'

`Empty mass` — Пустая масса
0.5 (значение по умолчанию) | скаляр

Пустая масса тела в виде двойного скаляра.

Программируемое использование

Параметры блоков: mass_e

Ввод: символьный вектор

Значения: двойной скаляр

Значение по умолчанию: '0.5'

`Full mass` — Полная масса тела
2.0 (значение по умолчанию) | скаляр

Полная масса тела в виде двойного скаляра.

Программируемое использование

Параметры блоков: mass_f

Ввод: символьный вектор

Значения: двойной скаляр

Значение по умолчанию: '2.0'

`Empty inertia matrix` — Пустая матрица инерции
`eye(3)` (значение по умолчанию) | 3х3 матрица

Матрица тензора инерции для пустой инерции тела в виде 3х3 матрицы.

Программируемое использование

Параметры блоков: inertia_e

Ввод: символьный вектор

Значения: 'eye(3)' | 3х3 матрица

Значение по умолчанию: 'eye(3)'

`Full inertia matrix` — Полная инерция тела
`2*eye(3)` (значение по умолчанию) | 3х3 матрица

Матрица тензора инерции для полной инерции тела в виде 3х3 матрицы.

Программируемое использование

Параметры блоков: inertia_f

Ввод: символьный вектор

Значения: '2*eye(3)' | 3х3 матрица

Значение по умолчанию: '2*eye(3)'

`Include mass flow relative velocity` — Массовый скоростной порт родственника потока
`off` (значение по умолчанию) | `on`

Установите этот флажок, чтобы добавить массовый скоростной порт родственника потока. Это - относительная скорость, при которой масса аккумулируется или удаляется.

Программируемое использование

Параметры блоков: vre_flag

Ввод: символьный вектор

Значения: off | on

Значение по умолчанию: off

`Include inertial acceleration` — Включайте инерционный ускоряющий порт
`off` (значение по умолчанию) | `on`

Установите этот флажок, чтобы добавить инерционный ускоряющий порт.

Зависимости

Чтобы включить порт _Abe, выберите этот параметр.

Программируемое использование

Параметры блоков: abi_flag

Ввод: символьный вектор

Значения: 'off' | 'on'

Значение по умолчанию: off

Атрибуты состояния

Присвойте уникальное имя каждому состоянию. Можно использовать имена состояния вместо путей к блоку во время линеаризации.

Чтобы присвоить имя к одному состоянию, введите уникальное имя между кавычками, например, 'velocity'.
Чтобы присвоить имена к нескольким состояниям, введите список, разделенный запятыми, окруженный фигурными скобками, например, {'a', 'b', 'c'}. Каждое имя должно быть уникальным.
Если параметр пуст (' '), никакое имя не присвоено.
Имена состояния применяются только к выбранному блоку параметром имени.
Количество состояний должно разделиться равномерно среди количества имен состояния.
Можно задать меньше имен, чем состояния, но вы не можете задать больше имен, чем состояния.
Например, можно задать два имени в системе с четырьмя состояниями. Имя применяется к первым двум состояниям и второму имени к последним двум состояниям.
Чтобы присвоить имена состояния с переменной в рабочей области MATLAB^®, введите переменную без кавычек. Переменная может быть вектором символов, массивом ячеек или структурой.

`Position: e.g., {'Xe', 'Ye', 'Ze'}` — Имя состояния положения
`''` (значение по умолчанию) | список, разделенный запятыми окружается фигурными скобками

Состояние положения называет в виде списка, разделенного запятыми окруженный фигурными скобками.

Программируемое использование

Параметры блоков: xme_statename

Ввод: символьный вектор

Значения: '' | список, разделенный запятыми окружается фигурными скобками

Значение по умолчанию: ''

`Velocity: e.g., {'U', 'v', 'w'}` — Скоростное имя состояния
`''` (значение по умолчанию) | список, разделенный запятыми окружается фигурными скобками

Скоростное состояние называет в виде списка, разделенного запятыми окруженный фигурными скобками.

Программируемое использование

Параметры блоков: Vm_statename

Ввод: символьный вектор

Значения: '' | список, разделенный запятыми окружается фигурными скобками

Значение по умолчанию: ''

`Euler rotation angles: e.g., {'phi', 'theta', 'psi'}` — Эйлерово имя состояния вращения
`''` (значение по умолчанию) | список, разделенный запятыми окружается фигурными скобками

Эйлерово состояние угла поворота называет в виде списка, разделенного запятыми окруженный фигурными скобками.

Программируемое использование

Параметры блоков: eul_statename

Ввод: символьный вектор

Значения: '' | список, разделенный запятыми окружается фигурными скобками

Значение по умолчанию: ''

`Body rotation rates: e.g., {'p', 'q', 'r'}` — Вращение тела утверждает имена
`''` (значение по умолчанию) | список, разделенный запятыми окружается фигурными скобками

Уровень вращения тела утверждает имена, заданный список, разделенный запятыми, окруженный фигурными скобками.

Программируемое использование

Параметры блоков: pm_statename

Ввод: символьный вектор

Значения: '' | список, разделенный запятыми окружается фигурными скобками

Значение по умолчанию: ''

`Mass: e.g., 'mass'` — Массовое имя состояния
`''` (значение по умолчанию) | вектор символов

Массовое имя состояния в виде вектора символов.

Программируемое использование

Параметры блоков: mass_statename

Ввод: символьный вектор

Значения: '' | вектор символов

Значение по умолчанию: ''

Алгоритмы

Источник зафиксированной телом координатной системы координат является центром тяжести тела, и тело принято, чтобы быть твердым, предположение, которое избавляет от необходимости рассматривать силы, действующие между отдельными элементами массы. Плоская Наземная система координат рассматривается инерционной, превосходное приближение, которое позволяет силам из-за движения Земли относительно фиксированных звезд быть пропущенными.

Поступательное движение зафиксированной телом координатной системы координат приведено ниже, где приложенные силы _{[Fx FyFz]} ^Tнаходятся в зафиксированной телом системе координат. Vre _b является относительной скоростью в осях тела в который массовый поток ( $\dot{m}$ ) извлекается или добавляется к телу в осях тела.

$\begin{array}{l} {\bar{F}}_{b} = [\begin{array}{l} F_{x} \\ F_{y} \\ F_{z} \end{array}] = m ({\dot{\bar{V}}}_{b} + \bar{ω} \times {\bar{V}}_{b}) + \dot{m} \bar{V} r e_{b} \\ A_{b e} = \frac{{\bar{F}}_{b} - \dot{m} {\bar{V}}_{r e}}{m} \\ A_{b b} = [\begin{matrix} {\dot{u}}_{b} \\ {\dot{v}}_{b} \\ {\dot{ω}}_{b} \end{matrix}] = \frac{{\bar{F}}_{b} - \dot{m} {\bar{V}}_{r e}}{m} - \bar{ω} \times {\bar{V}}_{b} \\ {\bar{V}}_{b} = [\begin{array}{l} u_{b} \\ v_{b} \\ w_{b} \end{array}], \bar{ω} = [\begin{array}{l} p \\ q \\ r \end{array}] \end{array}$

Вращательные движущие силы зафиксированной телом системы координат приведены ниже, где прикладными моментами является [L _MN] ^T, и тензор инерции, I относительно источника O.

$\begin{array}{l} {\bar{M}}_{B} = [\begin{array}{l} L \\ M \\ N \end{array}] = I \dot{\bar{ω}} + \bar{ω} \times (I \bar{ω}) + \dot{I} \bar{ω} \\ I = [\begin{array}{l} I_{x x} & - I_{x y} & - I_{x z} \\ - I_{y x} & I_{y y} & - I_{y z} \\ - I_{z x} & - I_{z y} & I_{z z} \end{array}] \end{array}$

Тензор инерции определяется с помощью поиска по таблице, который линейно интерполирует между _Ifull и _Iempty на основе массы (m). В то время как скорость изменения тензора инерции оценивается следующим уравнением.

$\dot{I} = \frac{I_{f u l l} - I_{e m p t y}}{m_{f u l l} - m_{e m p t y}} \dot{m}$

Отношение между зафиксированным телом вектором скорости вращения, [p q r] ^T, и скоростью изменения Углов Эйлера, [ $\dot{ϕ} \dot{θ} \dot{ψ}$ ] ^T, может быть определен путем решения Эйлеровых уровней в зафиксированную телом координатную систему координат.

$[\begin{array}{l} p \\ q \\ r \end{array}] = [\begin{array}{l} \dot{ϕ} \\ 0 \\ 0 \end{array}] + [\begin{array}{l} 1 & 0 & 0 \\ 0 & \cos ϕ & \sin ϕ \\ 0 & - \sin ϕ & \cos ϕ \end{array}] [\begin{array}{l} 0 \\ \dot{θ} \\ 0 \end{array}] + [\begin{array}{l} 1 & 0 & 0 \\ 0 & \cos ϕ & \sin ϕ \\ 0 & - \sin ϕ & \cos ϕ \end{array}] [\begin{array}{l} \cos θ & 0 & - \sin θ \\ 0 & 1 & 0 \\ \sin θ & 0 & \cos θ \end{array}] [\begin{array}{l} 0 \\ 0 \\ \dot{ψ} \end{array}] \equiv J^{- 1} [\begin{array}{l} \dot{ϕ} \\ \dot{θ} \\ \dot{ψ} \end{array}]$

Инвертирование J затем дает необходимое отношение, чтобы определить Эйлеров вектор уровня.

$[\begin{array}{l} \dot{ϕ} \\ \dot{θ} \\ \dot{ψ} \end{array}] = J [\begin{array}{l} p \\ q \\ r \end{array}] = [\begin{array}{l} 1 & (\sin ϕ \tan θ) & (\cos ϕ \tan θ) \\ 0 & \cos ϕ & - \sin ϕ \\ 0 & \frac{\sin ϕ}{\cos θ} & \frac{\cos ϕ}{\cos θ} \end{array}] [\begin{array}{l} p \\ q \\ r \end{array}]$

Ссылки

[1] Стивенс, Брайан и Франк Льюис. Управление самолетом и Симуляция. 2-й редактор Хобокен, NJ: John Wiley & Sons, 2003.

[2] Zipfel, Питер Х. Моделинг и Симуляция Космической Динамики аппарата. 2-й редактор Рестон, ВА: Образовательный Ряд AIAA, 2007.

Расширенные возможности

Генерация кода C/C++
Генерация кода C и C++ с помощью Simulink® Coder™.

Введен в R2006a

Документация

Simple Variable Mass 6DOF (Euler Angles)

Описание

Ограничения

Порты

Входной параметр

Fxyz — Приложенные силы трехэлементный вектор

Mxyz(N-m) — Прикладные моменты трехэлементный вектор

dm/dt (kg/s) — Скорость изменения массы скаляр

Vre — Относительная скорость трехэлементный вектор

Зависимости

Вывод

Ve — Скорость в плоской Наземной системе координат трехэлементный вектор

Xe — Положение в плоской Наземной системе координат трехэлементный вектор

φ θ ψ (rad) — Эйлеровы углы поворота трехэлементный вектор

DCMbe — Координатное преобразование 3х3 матрица

Vb — Скорость в зафиксированной телом системе координат трехэлементный вектор

ωb (rad/s) — Угловые уровни в зафиксированных телом осях трехэлементный вектор

dωb/dt — Угловые ускорения трехэлементный вектор

Abb — Ускорения в зафиксированных телом осях трехэлементный вектор

Fuel — Состояние топливного бака скаляр

Abe — Ускорения относительно инерционной системы координат трехэлементный вектор

Зависимости

Параметры

Основной

Units — Модули ввода и вывода Metric (MKS) (значение по умолчанию) | English (Velocity in ft/s) | English (Velocity in kts)

Программируемое использование

Mass Type — Массовый тип Simple Variable (значение по умолчанию) | Fixed | Custom Variable

Программируемое использование

Representation — Уравнения представления движения Euler Angles (значение по умолчанию) | Quaternion

Программируемое использование

Initial position in inertial axes [Xe,Ye,Ze] — Положение в инерционных осях[0 0 0] (значение по умолчанию) | трехэлементный вектор

Программируемое использование

Initial velocity in body axes [U,v,w] — Скорость в осях тела[0 0 0] (значение по умолчанию) | трехэлементный вектор

Программируемое использование

Initial Euler orientation [roll, pitch, yaw] — Начальная Эйлерова ориентация[0 0 0] (значение по умолчанию) | трехэлементный вектор

Программируемое использование

Initial body rotation rates [p,q,r] — Начальное вращение тела[0 0 0] (значение по умолчанию) | трехэлементный вектор

Программируемое использование

Initial mass — Начальная масса1.0 (значение по умолчанию) | скаляр

Программируемое использование

Empty mass — Пустая масса0.5 (значение по умолчанию) | скаляр

Программируемое использование

Full mass — Полная масса тела2.0 (значение по умолчанию) | скаляр

Программируемое использование

Empty inertia matrix — Пустая матрица инерции eye(3) (значение по умолчанию) | 3х3 матрица

Программируемое использование

Full inertia matrix — Полная инерция тела 2*eye(3) (значение по умолчанию) | 3х3 матрица

Программируемое использование

Include mass flow relative velocity — Массовый скоростной порт родственника потока off (значение по умолчанию) | on

Программируемое использование

Include inertial acceleration — Включайте инерционный ускоряющий порт off (значение по умолчанию) | on

Зависимости

Программируемое использование

Атрибуты состояния

Position: e.g., {'Xe', 'Ye', 'Ze'} — Имя состояния положения '' (значение по умолчанию) | список, разделенный запятыми окружается фигурными скобками

Программируемое использование

Velocity: e.g., {'U', 'v', 'w'} — Скоростное имя состояния '' (значение по умолчанию) | список, разделенный запятыми окружается фигурными скобками

Программируемое использование

Euler rotation angles: e.g., {'phi', 'theta', 'psi'} — Эйлерово имя состояния вращения '' (значение по умолчанию) | список, разделенный запятыми окружается фигурными скобками

Программируемое использование

Body rotation rates: e.g., {'p', 'q', 'r'} — Вращение тела утверждает имена '' (значение по умолчанию) | список, разделенный запятыми окружается фигурными скобками

Программируемое использование

Mass: e.g., 'mass' — Массовое имя состояния '' (значение по умолчанию) | вектор символов

Программируемое использование

Алгоритмы

Ссылки

Расширенные возможности

Генерация кода C/C++ Генерация кода C и C++ с помощью Simulink® Coder™.

Смотрите также

Документация Aerospace Blockset

Поддержка

`_Fxyz` — Приложенные силы
трехэлементный вектор

`_Mxyz(N-m)` — Прикладные моменты
трехэлементный вектор

`dm/dt (kg/s)` — Скорость изменения массы
скаляр

`_Vre` — Относительная скорость
трехэлементный вектор

`_Ve` — Скорость в плоской Наземной системе координат
трехэлементный вектор

`_Xe` — Положение в плоской Наземной системе координат
трехэлементный вектор

`φ θ ψ (rad)` — Эйлеровы углы поворота
трехэлементный вектор

`_DCMbe` — Координатное преобразование
3х3 матрица

`_Vb` — Скорость в зафиксированной телом системе координат
трехэлементный вектор

`_{ωb (rad/s)}` — Угловые уровни в зафиксированных телом осях
трехэлементный вектор

`_dωb/dt` — Угловые ускорения
трехэлементный вектор

`_Abb` — Ускорения в зафиксированных телом осях
трехэлементный вектор

`Fuel` — Состояние топливного бака
скаляр

`_Abe` — Ускорения относительно инерционной системы координат
трехэлементный вектор

`Units` — Модули ввода и вывода
`Metric (MKS)` (значение по умолчанию) | `English (Velocity in ft/s)` | `English (Velocity in kts)`

`Mass Type` — Массовый тип
`Simple Variable` (значение по умолчанию) | `Fixed` | `Custom Variable`

`Representation` — Уравнения представления движения
`Euler Angles` (значение по умолчанию) | `Quaternion`

`Initial position in inertial axes [Xe,Ye,Ze]` — Положение в инерционных осях
[0 0 0] (значение по умолчанию) | трехэлементный вектор

`Initial velocity in body axes [U,v,w]` — Скорость в осях тела
[0 0 0] (значение по умолчанию) | трехэлементный вектор

`Initial Euler orientation [roll, pitch, yaw]` — Начальная Эйлерова ориентация
[0 0 0] (значение по умолчанию) | трехэлементный вектор

`Initial body rotation rates [p,q,r]` — Начальное вращение тела
[0 0 0] (значение по умолчанию) | трехэлементный вектор

`Initial mass` — Начальная масса
1.0 (значение по умолчанию) | скаляр

`Empty mass` — Пустая масса
0.5 (значение по умолчанию) | скаляр

`Full mass` — Полная масса тела
2.0 (значение по умолчанию) | скаляр

`Empty inertia matrix` — Пустая матрица инерции
`eye(3)` (значение по умолчанию) | 3х3 матрица

`Full inertia matrix` — Полная инерция тела
`2*eye(3)` (значение по умолчанию) | 3х3 матрица

`Include mass flow relative velocity` — Массовый скоростной порт родственника потока
`off` (значение по умолчанию) | `on`

`Include inertial acceleration` — Включайте инерционный ускоряющий порт
`off` (значение по умолчанию) | `on`

`Position: e.g., {'Xe', 'Ye', 'Ze'}` — Имя состояния положения
`''` (значение по умолчанию) | список, разделенный запятыми окружается фигурными скобками

`Velocity: e.g., {'U', 'v', 'w'}` — Скоростное имя состояния
`''` (значение по умолчанию) | список, разделенный запятыми окружается фигурными скобками

`Euler rotation angles: e.g., {'phi', 'theta', 'psi'}` — Эйлерово имя состояния вращения
`''` (значение по умолчанию) | список, разделенный запятыми окружается фигурными скобками

`Body rotation rates: e.g., {'p', 'q', 'r'}` — Вращение тела утверждает имена
`''` (значение по умолчанию) | список, разделенный запятыми окружается фигурными скобками

`Mass: e.g., 'mass'` — Массовое имя состояния
`''` (значение по умолчанию) | вектор символов

Генерация кода C/C++
Генерация кода C и C++ с помощью Simulink® Coder™.