В этом примере показано, как аппроксимировать задержки системного использования разомкнутого контура непрерывного времени pade.
Приближение Padé полезно при использовании анализа или Design Tool, которые не поддерживают задержки.
Создайте демонстрационную систему разомкнутого контура с выходной задержкой.
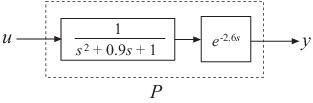
s = tf('s');
P = exp(-2.6*s)/(s^2+0.9*s+1);P передаточная функция второго порядка (tf) объект с задержкой.
Вычислите приближение Padé первого порядка P.
Pnd1 = pade(P,1)
Pnd1 =
-s + 0.7692
----------------------------------
s^3 + 1.669 s^2 + 1.692 s + 0.7692
Continuous-time transfer function.
Эта команда заменяет все задержки P приближением первого порядка. Поэтому Pnd1 передаточная функция третьего порядка без задержек.
Сравните частотную характеристику исходного и аппроксимированного использования моделей bodeplot.
h = bodeoptions; h.PhaseMatching = 'on'; bodeplot(P,'-b',Pnd1,'-.r',{0.1,10},h) legend('Exact delay','First-Order Pade','Location','SouthWest')

Величина P и Pnd1 соответствуйте точно. Однако фаза Pnd1 отклоняется от фазы P вне приблизительно 1 рад/с.
Увеличьте порядок приближения Padé расширить диапазон частот, в котором приближение фазы хорошо.
Pnd3 = pade(P,3);
Сравните частотную характеристику P, Pnd1 и Pnd3.
bodeplot(P,'-b',Pnd3,'-.r',Pnd1,':k',{0.1 10},h) legend('Exact delay','Third-Order Pade','First-Order Pade',... 'Location','SouthWest')

Ошибка приближения фазы уменьшается при помощи третьего порядка приближение Padé.
Сравните ответы области времени исходного и аппроксимированного системного использования stepplot.
stepplot(P,'-b',Pnd3,'-.r',Pnd1,':k') legend('Exact delay','Third-Order Pade','First-Order Pade',... 'Location','Southeast')

Используя Padé приближение вводит неминимальный артефакт фазы (“неправильный путь” эффект) в начальном переходном процессе. Эффект вполне объявлен в приближении первого порядка, которое опускается значительно ниже нуля прежде, чем изменить направление. Эффект уменьшается в приближении высшего порядка, которое намного более тесно совпадает с ответом точной системы.
Примечание
Используя слишком высокое приближение порядок может привести к числовым проблемам и возможно нестабильным полюсам. Поэтому избегайте приближений Padé с N> 10 порядка.