Используя InputDelay, OutputDelay, и ioDelay свойства, можно смоделировать простые процессы с транспортными задержками. Однако эти свойства не могут смоделировать более комплексные ситуации, такие как обратная связь с задержками. В дополнение к InputDelay и OutputDelay свойства, пространство состояний (ss) модели имеют InternalDelay свойство. Это свойство позволяет вам смоделировать соединение систем с входом, вывести или транспортировать задержки, включая обратную связь с задержками. Можно использовать InternalDelay свойство точно смоделировать и анализировать произвольные линейные системы с задержками. Внутренние задержки могут явиться результатом следующего:
Конкатенация моделей в пространстве состояний с задержками ввода и вывода.
Возвращение задержанного сигнала.
Преобразование MIMO tf или zpk модели с транспортными задержками с формой пространства состояний.
Используя внутренние задержки, можно сделать следующее:
В непрерывное время сгенерируйте безаппроксимированное время и симуляции частоты, потому что задержки не должны быть заменены приближением Padé. В непрерывное время это допускает более точный анализ систем с длительными задержками.
В дискретное время разделите задержки от другой системной динамики, потому что задержки не заменяются полюсами в z = 0, который повышает КПД времени и симуляций частоты для систем дискретного времени с длительными задержками.
Используйте большинство функций Control System Toolbox™.
Протестируйте усовершенствованные стратегии управления на задержанные системы. Например, можно реализовать и протестировать точную модель предиктора Смита. Смотрите Управление в качестве примера Процессов с Долгой Потерей времени: Предиктор Смита.
Этот пример иллюстрирует, почему введенный, выход, и транспорт задерживается недостаточно, чтобы смоделировать все типы задержек, которые могут возникнуть в динамических системах. Рассмотрите простую обратную связь с 2 задержками с:
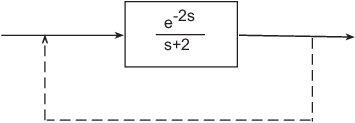
Передаточная функция с обратной связью
Термин задержки в числителе может быть представлен как выходная задержка. Однако термин задержки в знаменателе не может. Для того, чтобы смоделировать эффект задержки на обратной связи, InternalDelay свойство необходимо, чтобы отслеживать внутреннюю связь между задержками и обычной динамикой.
Как правило, вы не создаете модели в пространстве состояний с внутренними задержками непосредственно, путем определения A, B, C и матриц D вместе с набором внутренних задержек. Скорее такие модели возникают, когда вы соединяете модели, имеющие задержки. Нет никакого ограничения на то, сколько задержек включено и как модели соединяются. Для примера создания внутренней задержки путем закрытия обратной связи смотрите закрывающуюся Обратную связь с Задержками.
Когда вы работаете с моделями, имеющими внутренние задержки, знать о следующем поведении:
Когда соединение моделей дает начало внутренним задержкам, программное обеспечение возвращается ss модель независимо от взаимосвязанных типов модели. Это происходит потому что только ss поддерживает внутренние задержки.
Программное обеспечение полностью поддерживает обратную связь. Можно перенести обратную связь вокруг любой системы с задержками.
При отображении ABC, и D матрицы, программное обеспечение обнуляет все задержки (создающий нулевой порядок приближение Padé). Это приближение происходит для отображения только, а не для вычислений с помощью модели.
Для некоторых систем обнуление задержек создает сингулярные алгебраические циклы, которые приводят или к неподходящим или к неточно указанным приближениям нулевой задержки. Для этих систем:
Ввод sys возвращает только размеры для матриц системы под названием sys.
Ввод sys.A производит ошибку.
Ограниченное отображение и ошибка не подразумевают проблему с моделью sys самостоятельно.
Пространство состояний возражает использованию обобщенные уравнения пространства состояний, чтобы отслеживать внутренние задержки. Концептуально, такие модели состоят из двух взаимосвязанных частей:
Установлена обычная модель в пространстве состояний H (s) с увеличенным вводом-выводом
Банк внутренних задержек.
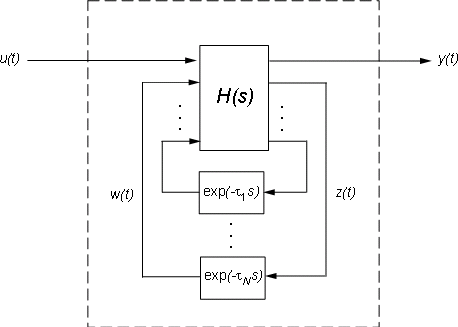
Соответствующие уравнения пространства состояний:
Вы не должны потрудиться этим внутренним представлением использовать инструменты. Если, однако, вы хотите извлечь H или матрицы A, B1, B2, ... , можно использовать getDelayModel, Для примера:
P = 5*exp(-3.4*s)/(s+1); C = 0.1 * (1 + 1/(5*s)); T = feedback(ss(P*C),1); [H,tau] = getDelayModel(T,'lft'); size(H)
Обратите внимание на то, что H 2D вход, 2D выходная модель тогда как T SISO. Обратная операция (комбинирующий H и tau создать T) выполняется setDelayModel.
Следующие команды поддерживают внутренние задержки и непрерывного - и системы дискретного времени:
Следующие команды поддерживают внутренние задержки и непрерывного - и системы дискретного времени и имеют определенные ограничения:
allmargin, margin— Интерполяция использования, поэтому эти команды только так же точны как тонкость заданной сетки.
pole, zero— Возвращает полюса и нули системы со всеми обнуленными задержками.
ssdata, get— Если модель SS имеет внутренние задержки, эти команды возвращают ABC, и D матрицы системы со всеми внутренними обнуленными задержками. Использование getDelayModel получить доступ к внутреннему представлению пространства состояний моделей с внутренними задержками.
Следующие команды не поддерживают внутренние задержки:
Анализ временного интервала —initial и initialplot
Проект компенсатора —rlocus, lqg, lqry, lqrd, kalman, kalmd, lqgreg, lqgtrack, lqi, и augstate.
Чтобы использовать эти функции в системе с внутренними задержками, использовать pade аппроксимировать внутренние задержки. Смотрите Приближение С временной задержкой.
[1] П. Гэхинет и Л.Ф. Шемпин, "Программное обеспечение для Моделирования и Анализа Линейных систем с Задержками", Proc. Американская Конференция Управления, Бостон, 2004, стр 5600-5605
[2] Л.Ф. Шемпин и П. Гэхинет, уравнения Делэ-дифферентиэл-алджебрэйка в Теории Управления, Прикладной Числовой Математике, 56 (2006), стр 574-588