Используя максимальную и ожидаемую максимальную просадку

Введение

Максимальная просадка является максимальным снижением ряда, измеренного, когда возвращаются, от пика до низшей точки в течение времени. Несмотря на то, что дополнительные метрики существуют, которые используются в хедж-фонде и сообществах торговли товарами (см. Педерсона и Радхолм-Алфвина [20] в Библиографии), исходное определение и последующая реализация этих метрик еще не стандартизированы.

Возможно вычислить аналитически ожидаемую максимальную просадку для Броуновского движения с дрейфом (см. Мэгдон-Исмаила, Atiya, Пратапа и Абу-Мустафу [16] Библиография). Эти результаты используются, чтобы оценить ожидаемую максимальную просадку для ряда, который приблизительно следует за геометрическим броуновским движением.

Использование maxdrawdown и emaxdrawdown вычислить максимальные и ожидаемые максимальные просадки.

Максимальная просадка

Этот пример демонстрирует, как вычислить максимальную просадку (MaxDD) с помощью наших данных в качестве примера с фондом, рынком и наличным рядом:

load FundMarketCash
MaxDD = maxdrawdown(TestData)

который дает следующие результаты:

MaxDD =
    0.1658    0.3381         0

Максимум заглядывает данному периоду времени, имел 16,58% для ряда фонда и 33,81% для рынка. Не было никакого снижения в наличном ряду, как ожидалось, потому что кассовый счет никогда не теряет значение.

maxdrawdown может также возвратить индексы (MaxDDIndex) из интервалов максимальной просадки для каждого ряда в дополнительном выходном аргументе:

[MaxDD, MaxDDIndex] = maxdrawdown(TestData)

который дает следующие результаты:

MaxDD =

    0.1658    0.3381         0


MaxDDIndex =

     2     2   NaN
    18    18   NaN

Первые два ряда испытывают свои максимальные просадки от второго до 18-го месяца в данных. Индексами для третьего ряда является NaNs, потому что это никогда не имеет спад.

Потеря значения на 16,58% с месяца 2 к месяцу 18 для ряда фонда проверяется с помощью индексов, о которых сообщают:

Start = MaxDDIndex(1,:);
End = MaxDDIndex(2,:);
(TestData(Start(1),1) - TestData(End(1),1))/TestData(Start(1),1)

ans =

    0.1658

Несмотря на то, что максимальная просадка измеряется в терминах возвратов, maxdrawdown может измерить спад в терминах абсолютного падения цены, или в терминах возвратов журнал. Чтобы контрастировать эти альтернативы более ясно, мы работаем с последовательным принятием фонда, начальными инвестициями 50 долларов:

Fund50 = 50*TestData(:,1);
plot(Fund50);
title('\bfFive-Year Fund Performance, Initial Investment 50 usd');
xlabel('Months');
ylabel('Value of Investment');

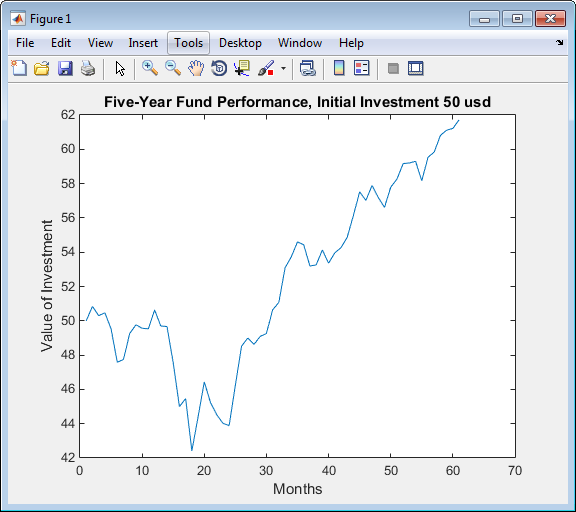
Во-первых, мы вычисляем стандартную максимальную просадку, которая совпадает с результатами выше, потому что возвраты независимы от начальных сумм, которые инвестируют:

MaxDD50Ret = maxdrawdown(Fund50)

MaxDD50Ret =

    0.1658

Затем мы вычисляем максимальное падение цены, с помощью arithmetic аргумент:

[MaxDD50Arith, Ind50Arith] = maxdrawdown(Fund50,'arithmetic')

MaxDD50Arith =

    8.4285


Ind50Arith =

     2
    18

Значение этих инвестиций составило 50,84$ в месяце 2, но к месяцу 18 значение составляло до 42,41$, отбрасывание 8,43$. Это - самая большая потеря в долларовой стоимости от предыдущего верхнего уровня в данном периоде времени. В этом случае период максимальной просадки, 2-й к 18-му месяцу, является тем же самым независимо от того, измеряется ли спад, когда возвращаются или как потеря долларовой стоимости.

Наконец, мы вычисляем максимальное снижение на основе возвратов журнал с помощью geometric аргумент. В этом примере возвращается результат возвратов журнал в максимальном отбрасывании 18,13%, снова от второго до 18-го месяца, недалеко от 16,58%, полученных с помощью стандарта.

[MaxDD50LogRet, Ind50LogRet] = maxdrawdown(Fund50,'geometric')

MaxDD50LogRet =

    0.1813


Ind50LogRet =

     2
    18

Отметьте, последняя мера эквивалентна нахождению арифметической максимальной просадки для журнала ряда:

MaxDD50LogRet2 = maxdrawdown(log(Fund50),'arithmetic')

MaxDD50LogRet2 =

    0.1813

Ожидаемая максимальная просадка

Этот пример демонстрирует использование моментов возврата журнал фонда, чтобы вычислить ожидаемую максимальную просадку (EMaxDD) и затем сравните его с реализованной максимальной просадкой (MaxDD).

load FundMarketCash
logReturns = log(TestData(2:end,:) ./ TestData(1:end - 1,:));
Mu = mean(logReturns(:,1));
Sigma = std(logReturns(:,1),1);
T = size(logReturns,1);

MaxDD = maxdrawdown(TestData(:,1),'geometric')
EMaxDD = emaxdrawdown(Mu, Sigma, T)

который дает следующие результаты:

MaxDD =

    0.1813


EMaxDD =

    0.1545

Спад, наблюдаемый в этом периоде времени, выше ожидаемой максимальной просадки. Здесь нет никакого противоречия. Ожидаемая максимальная просадка не является верхней границей на максимальных потерях от пика, но оценкой их среднего значения, на основе предположения геометрического броуновского движения.

Документация