Якобиан измерения функционирует для постоянного движения угловой скорости вращения
measurementjac = ctmeasjac(state)measurementjac, для постоянной модели движения Фильтра Калмана угловой скорости вращения в прямоугольных координатах. state задает текущее состояние дорожки.
measurementjac = ctmeasjac(state,frame)frame.
measurementjac = ctmeasjac(state,frame,sensorpos)sensorpos.
measurementjac = ctmeasjac(state,frame,sensorpos,sensorvel)sensorvel.
measurementjac = ctmeasjac(state,measurementParameters)measurementParameters.
Задайте состояние объекта в 2D постоянном движении угловой скорости вращения. Состояние является положением и скоростью в каждой размерности и угловой скоростью вращения. Создайте якобиан измерения в прямоугольных координатах.
state = [1;10;2;20;5]; jacobian = ctmeasjac(state)
jacobian = 3×5
1 0 0 0 0
0 0 1 0 0
0 0 0 0 0
Задайте состояние объекта в 2D постоянном движении угловой скорости вращения. Состояние является положением и скоростью в каждой размерности и угловой скоростью вращения. Вычислите якобиан измерения относительно сферических координат.
state = [1;10;2;20;5];
measurementjac = ctmeasjac(state,'spherical')measurementjac = 4×5
-22.9183 0 11.4592 0 0
0 0 0 0 0
0.4472 0 0.8944 0 0
0.0000 0.4472 0.0000 0.8944 0
Задайте состояние объекта в 2D постоянном движении угловой скорости вращения. Состояние является положением и скоростью в каждой размерности и угловой скоростью вращения. Вычислите якобиан измерения относительно сферических координат, сосредоточенных в [5;-20;0].
state = [1;10;2;20;5];
sensorpos = [5;-20;0];
measurementjac = ctmeasjac(state,'spherical',sensorpos)measurementjac = 4×5
-2.5210 0 -0.4584 0 0
0 0 0 0 0
-0.1789 0 0.9839 0 0
0.5903 -0.1789 0.1073 0.9839 0
Задайте состояние объекта в 2D постоянном движении угловой скорости вращения. Состояние является положением и скоростью в каждой размерности и угловой скоростью вращения. Вычислите якобиан измерения относительно сферических координат, сосредоточенных в [25;-40;0].
state2d = [1;10;2;20;5];
sensorpos = [25,-40,0].';
frame = 'spherical';
sensorvel = [0;5;0];
laxes = eye(3);
measurementjac = ctmeasjac(state2d,frame,sensorpos,sensorvel,laxes)measurementjac = 4×5
-1.0284 0 -0.5876 0 0
0 0 0 0 0
-0.4961 0 0.8682 0 0
0.2894 -0.4961 0.1654 0.8682 0
Поместите параметры измерения в структуру и используйте альтернативный синтаксис.
measparm = struct('Frame',frame,'OriginPosition',sensorpos,'OriginVelocity',sensorvel, ... 'Orientation',laxes); measurementjac = ctmeasjac(state2d,measparm)
measurementjac = 4×5
-1.0284 0 -0.5876 0 0
0 0 0 0 0
-0.4961 0 0.8682 0 0
0.2894 -0.4961 0.1654 0.8682 0
state — Вектор состоянияВектор состояния для постоянной модели движения угловой скорости вращения в двух или трех пространственных размерностях в виде вектора с действительным знаком или матрицы.
Когда задано как вектор с 5 элементами, вектор состояния описывает 2D движение в плоскости x-y. Можно задать вектор состояния как строку или вектор-столбец. Компонентами вектора состояния является [x;vx;y;vy;omega] где x представляет x - координата и vx представляет скорость в x - направление. y представляет y - координата и vy представляет скорость в y - направление. omega представляет угловую скорость вращения.
Когда задано как 5 N матрицей, каждый столбец представляет различный вектор состояния, N представляет количество состояний.
Когда задано как вектор с 7 элементами, вектор состояния описывает 3-D движение. Можно задать вектор состояния как строку или вектор-столбец. Компонентами вектора состояния является [x;vx;y;vy;omega;z;vz] где x представляет x - координата и vx представляет скорость в x - направление. y представляет y - координата и vy представляет скорость в y - направление. omega представляет угловую скорость вращения. z представляет z - координата и vz представляет скорость в z - направление.
Когда задано как 7 N матрицей, каждый столбец представляет различный вектор состояния. N представляет количество состояний.
Координаты положения исчисляются в метрах. Скоростные координаты находятся в метрах/секунда. Угловая скорость вращения находится в степенях/секунда.
Пример: [5;0.1;4;-0.2;0.01]
Типы данных: double
frame — Measurement система координат выхода'rectangular' (значение по умолчанию) | 'spherical'Measurement система координат выхода в виде 'rectangular' или 'spherical'. Когда системой координат является 'rectangular', измерение состоит из x, y и Декартовых координат z. Когда задано как 'spherical', измерение состоит из азимута, вертикального изменения, области значений и уровня области значений.
Типы данных: char
sensorpos — Положение датчикаПоложение датчика относительно навигации структурирует в виде вектор-столбца 3 на 1 с действительным знаком. Модули исчисляются в метрах.
Типы данных: double
sensorvel — Скорость датчикаСкорость датчика относительно навигации структурирует в виде вектор-столбца 3 на 1 с действительным знаком. Модули находятся в m/s.
Типы данных: double
laxes — Локальные оси координат датчикаЛокальные оси координат датчика в виде 3х3 ортогональной матрицы. Каждый столбец задает направление локального x - y - и z - оси, соответственно, относительно системы координат навигации. Таким образом, матрица является матрицей вращения от глобальной системы координат до системы координат датчика.
Типы данных: double
measurementParameters — Параметры измеренияПараметры измерения в виде структуры или массива структур. Поля структуры:
| Поле | Описание | Пример |
|---|---|---|
Frame | Система координат раньше сообщала об измерениях в виде одного из этих значений:
| 'spherical' |
OriginPosition | Смещение положения источника системы координат относительно родительской системы координат в виде [x y z] вектор с действительным знаком. | [0 0 0] |
OriginVelocity | Скоростное смещение источника системы координат относительно родительской системы координат в виде [vx vy vz] вектор с действительным знаком. | [0 0 0] |
Orientation | Структурируйте матрицу вращения в виде 3х3 ортонормированной матрицы с действительным знаком. | [1 0 0; 0 1 0; 0 0 1] |
HasAzimuth | Логический скаляр, указывающий, включен ли азимут в измерение. | 1 |
HasElevation | Логический скаляр, указывающий, включено ли вертикальное изменение в измерение. Для измерений, о которых сообщают в прямоугольной системе координат, и если HasElevation является ложным, измерения, о которых сообщают, принимают 0 градусов вертикального изменения. | 1 |
HasRange | Логический скаляр, указывающий, включена ли область значений в измерение. | 1 |
HasVelocity | Логический скаляр, указывающий, включают ли обнаружения, о которых сообщают, скоростные измерения. Для измерений, о которых сообщают в прямоугольной системе координат, если HasVelocity является ложным, об измерениях сообщают как [x y z]. Если HasVelocity true, об измерениях сообщают как [x y z vx vy vz]. | 1 |
IsParentToChild | Логический скаляр, указывающий, если Orientation выполняет вращение системы координат от системы координат координаты вышестоящего элемента до системы координат координаты нижестоящего элемента. Когда IsParentToChild false, затем Orientation выполняет вращение системы координат от системы координат координаты нижестоящего элемента до системы координат координаты вышестоящего элемента. | 0 |
Типы данных: struct
measurementjac — Якобиан измеренияЯкобиан измерения, возвращенный как 3 на 5 с действительным знаком или 4 5 матрица. Размерность строки и интерпретация зависят от значения frame аргумент.
| Система координат | Якобиан измерения |
|---|---|
'rectangular' | Якобиан измерений [x;y;z] относительно вектора состояния. Вектор измерения относительно системы локальной координаты. Координаты исчисляются в метрах. |
'spherical' | Якобиан вектора измерения [az;el;r;rr] относительно вектора состояния. Компоненты вектора измерения задают угол азимута, угол возвышения, область значений и уровень области значений объекта относительно локальной системы координат датчика. Угловые модули в градусах. Модули области значений исчисляются в метрах и располагаются, модули уровня находятся в метрах/секунда. |
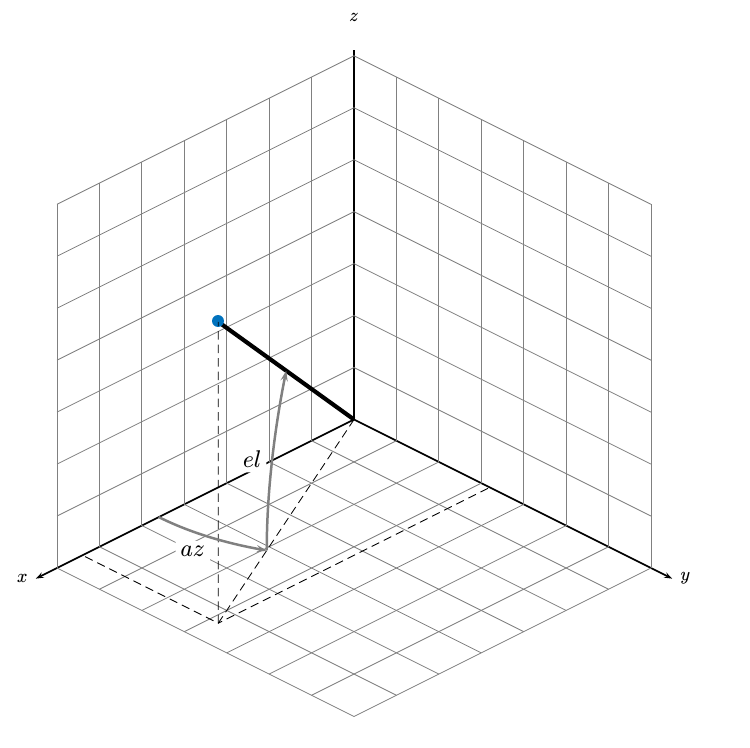
Задайте азимут и углы возвышения, используемые в Sensor Fusion and Tracking Toolbox™.
azimuth angle вектора является углом между x - ось и ее ортогональной проекцией на плоскость xy. Угол положителен в движении от оси x к оси y. Углы азимута находятся между –180 и 180 градусами. elevation angle является углом между вектором и его ортогональной проекцией на xy - плоскость. Угол положителен при движении к положительному z - ось от плоскости xy.
cameas | cameasjac | constacc | constaccjac | constturn | constturnjac | constvel | constveljac | ctmeas | cvmeas | cvmeasjacУ вас есть модифицированная версия этого примера. Вы хотите открыть этот пример со своими редактированиями?
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.