Оптимизация является процессом нахождения точки, которая минимизирует функцию. Более в частности:
Минимум local функции является точкой, где значение функции меньше, чем или равно значению в соседних точках, но возможно больше, чем в удаленной точке.
Минимум global является точкой, где значение функции меньше, чем или равно значению во всех других допустимых точках.
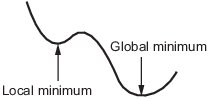
Обычно решатели Optimization Toolbox™ находят локальный оптимум. (Этот локальный оптимум может быть глобальным оптимумом.) Они находят оптимум в basin of attraction начальной точки. Для получения дополнительной информации смотрите Области притяжения.
В отличие от этого решатели Global Optimization Toolbox спроектированы, чтобы перерыть больше чем одну область притяжения. Они ищут в различных способах:
GlobalSearch и MultiStart сгенерируйте много начальных точек. Они затем используют локальный решатель, чтобы найти optima в областях притяжения начальных точек.
ga использует набор начальных точек (названный населением) и итеративно генерирует лучшие точки от населения. Пока начальная генеральная совокупность покрывает несколько областей, ga может исследовать несколько областей.
particleswarm, как ga, использует набор начальных точек. particleswarm может исследовать несколько областей целиком из-за его разнообразного населения.
simulannealbnd выполняет случайный поиск. Обычно simulannealbnd принимает точку, если это лучше, чем предыдущая точка. simulannealbnd иногда принимает худшую точку, для того, чтобы достигнуть различной области.
patternsearch взгляды на многие соседние точки прежде, чем принять один из них. Если некоторые соседние точки принадлежат различным областям, patternsearch в сущности взгляды во многих областях целиком.
surrogateopt начинается квазислучайной выборкой внутри границ, ища маленькое значение целевой функции. surrogateopt использует merit function, который, частично, дает настройку точкам, которые далеки от оцененных точек, который является попыткой достигнуть глобального решения. После того, как это не может улучшить текущую точку, surrogateopt сброс, вызывая его к выборке широко внутри границ снова. Сброс иначе surrogateopt поиски глобального решения.
Если целевая функция, которой f (x) является гладким, вектор – ∇f (x), указывает в направлении, где f (x) уменьшается наиболее быстро. Уравнение наискорейшего спуска, а именно,
дает путь x (t), который приводит к локальному минимуму, когда t становится большим. Обычно x начальных значений (0), которые являются друг близко к другу, дает наикратчайшие пути, которые стремятся к той же минимальной точке. basin of attraction для наискорейшего спуска является набором продвижения начальных значений к тому же локальному минимуму.
Следующий рисунок показывает два одномерных минимума. Рисунок показывает различные области притяжения с различными стилями линии, и это показывает направления наискорейшего спуска стрелками. Для этого и последующих фигур, черные точки представляют локальные минимумы. Каждый наикратчайший путь, x начинающийся в точке (0), идет к черной точке в области, содержащей x (0).
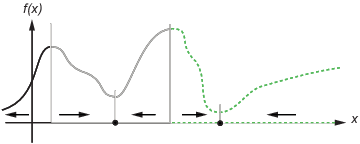
Следующий рисунок показывает, как наикратчайшие пути могут быть более сложными в большем количестве размерностей.
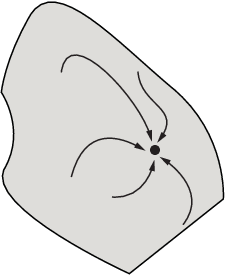
Следующий рисунок показывает еще более сложные пути и области притяжения.

Ограничения могут разбить одну область притяжения в несколько частей. Например, рассмотрите минимизацию y, удовлетворяющий:
y ≥ |x |
y ≥ 5 – 4 (x –2) 2.
Рисунок показывает эти две области притяжения с конечными точками.
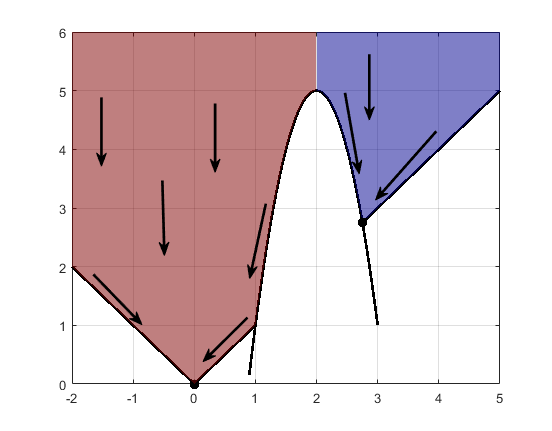
Наикратчайшие пути являются прямыми линиями вниз к границам ограничений. От границ ограничений наикратчайшие пути перемещаются вниз вдоль контуров. Конечная точка или (0,0) или (11/4,11/4), в зависимости от того, является ли начальный x - значение выше или ниже 2.