Поляризованные поля

Введение в поляризацию

Можно использовать программное обеспечение Phased Array System Toolbox™, чтобы симулировать радиолокационные системы, которые передают, распространяют, отражают и получают поляризованные электромагнитные поля. Включением этой возможности тулбокс может реалистично смоделировать взаимодействие радарных волн с целями и средой.

Это - основное свойство плоских волн в свободном пространстве, что направления векторов электрического и магнитного поля являются ортогональными к их направлению распространения. Направление распространения электромагнитной волны определяется вектором Poynting

$S = E \times H$

В этом уравнении E представляет электрическое поле, и H представляет магнитное поле. Количество, S, представляет величину и направление энергетического потока волны. Уравнения Максвелла, когда применился к плоским волнам, приводят к результату, которым связаны электрические и магнитные поля

$\begin{array}{l} E & = - Z s \times H \\ H & = \frac{1}{Z} s \times E \end{array}$

Векторный s, единичный вектор в направлении S, представляет направление распространения волны. Количество, Z, является wave impedance и является функцией электрической проницаемости и магнитной проницаемостью носителя, в котором перемещается волна.

После управления этими двумя уравнениями вы видите, что электрические и магнитные поля являются ортогональными к направлению распространения

$E \cdot s = H \cdot s = 0.$

Этот последний результат доказывает, что существует действительно только два независимых компонента электрического поля, пометил _Ex и _Ey. Точно так же магнитное поле может быть описано в терминах двух независимых компонентов. Из-за ортогональности полей электрическое поле может быть представлено в терминах двух единичных векторов, ортогональных к направлению распространения.

$E = E_{x} {\hat{e}}_{x} + E_{y} {\hat{e}}_{y}$

Единичные векторы вместе с единичным вектором в направлении распространения

${{\hat{e}}_{x}, {\hat{e}}_{y}, s} .$

сформируйте предназначенную для правой руки ортонормированную триаду. Позже, эти векторы и координаты, которые они задают, будут связаны с координатами определенной радиолокационной системы. В радиолокационных системах распространено использовать индексы, H и V, обозначая горизонтальные и вертикальные составляющие, вместо x и y. Поскольку электрические и магнитные поля определяются друг другом, только свойства электрического поля должны быть, рассматривают.

Для радиолокационной системы электрическое и магнитное поле является на самом деле сферическими волнами, а не плоскими волнами. Однако на практике эти поля обычно измеряются в далекой полевой области или зоне излучения радарного источника и являются приблизительно плоскими волнами. В далеком поле волны называются волнами quasi-plane. Точка находится в far field, если его расстояние, R, из источника удовлетворяют ^{R ≫D2/λ}, где D является типичной размерностью источника, является ли это одной антенной или массивом антенн.

Поляризация применяется к чисто синусоидальным сигналам. Самое общее выражение для синусоидальной плоской волны имеет форму

$E = E_{x 0} \cos (ω t - k \cdot x + ϕ_{x}) {\hat{e}}_{x} + E_{y 0} \cos (ω t - k \cdot x + ϕ_{y}) {\hat{e}}_{y} = E_{x} {\hat{e}}_{x} + E_{y} {\hat{e}}_{y}$

Количества _Ex0 и _Ey0 являются с действительным знаком, неотрицательным, амплитудами компонентов электрического поля и _ϕx и _ϕy, являются фазами поля. Это выражение является самым общим, используемым для поляризованной волны. Электромагнитной волной является polarized, если отношение амплитуд его компонентов и разности фаз между ним компоненты не изменяется со временем. Определение поляризации может быть расширено, чтобы включать сигналы narrowband, для которых пропускная способность мала по сравнению с центром или несущей частотой сигнала. Амплитудное отношение и различие в фазах варьируются медленно со временем, когда по сравнению с периодом волны и может считаться постоянным по многим колебаниям.

Можно обычно подавлять пространственную зависимость поля и писать вектор электрического поля как

$E = E_{x 0} \cos (ω t + ϕ_{x}) {\hat{e}}_{x} + E_{y 0} \cos (ω t + ϕ_{y}) {\hat{e}}_{y} = E_{x} {\hat{e}}_{x} + E_{y} {\hat{e}}_{y}$

Линейная и круговая поляризация

Предыдущее уравнение для поляризованной плоской волны показывает, что совет двумерного вектора электрического поля проходит путь, который находится в плоскости, ортогональной к направлению поля распространения. Форма пути зависит от величин и фаз компонентов. Например, если _ϕx = _ϕy, можно удалить временную зависимость и запись

$E_{y} = \frac{E_{y 0}}{E_{x 0}} E_{x}$

Это уравнение представляет прямую линию через начало координат с положительным наклоном. С другой стороны предположите _{ϕx = ϕy + π}. Затем совет вектора электрического поля следует за прямой линией через начало координат с отрицательным наклоном

$E_{y} = - \frac{E_{y 0}}{E_{x 0}} E_{x}$

Эти два случая поляризации называют linear polarized, потому что поле всегда колеблется вдоль прямой линии в ортогональной плоскости. Если _{Ex0= 0}, полем является vertically polarized, и если _{Ey0 = 0} поле является horizontally polarized.

Различный случай происходит, когда амплитуды являются тем же самым, _Ex = _Ey, но фазы отличаются ±π/2

$\begin{array}{l} E_{x} & = E_{0} \cos (ω t + ϕ) \\ E_{y} & = E_{0} \cos (ω t + ϕ \pm π / 2) = \mp E_{0} \sin (ω t + ϕ) \end{array}$

Путем обработки на квадрат обеим сторонам можно показать, что совет вектора электрического поля выполняет уравнение круга

$E_{x}^{2} + E_{y}^{2} = E_{0}^{2}$

В то время как это уравнение дает путь, вектор берет, это не говорит вам в том, какое направление вектор электрического поля перемещается вокруг круга. Это вращается по часовой стрелке или против часовой стрелки? Направление вращения зависит от знака π/2 в фазе. Вы видите эту зависимость путем исследования движения совета векторного поля. Примите общий угол фазы, ϕ = 0. Это предположение допустимо, потому что общая фаза только определяет стартовую позицию вектора и не изменяет форму его пути. Во-первых, посмотрите на случай +π/2 для волны, перемещающейся вдоль s - направление (из страницы). В t=0 вектор указывает вдоль x - ось. Один период четверти позже, вектор указывает вдоль отрицательной оси y-. После другого периода четверти это указывает вдоль отрицательной оси x-.

MATLAB^® использует соглашение IEEE присвоить имена поляризация, выполненная левой рукой, или выполненная правой рукой, направлению вращения электрического вектора, а не по часовой стрелке или против часовой стрелки. При использовании этого соглашения левая или правая хиральность определяется путем обращения левого или правого ползунка вдоль направления распространения волны. Затем выровняйте кривую пальцев к направлению вращения поля в данной точке на пробеле. Если вращение следует за кривой вашей левой руки, то волна предназначена для левой руки поляризованный. Если вращение следует за кривой вашей правой руки, то волна предназначена для правой руки поляризованный. В предыдущем сценарии поле является предназначенным для левой руки циркулярным поляризованным (LHCP). Разность фаз –π/2 соответствует предназначенной для правой руки циркулярной поляризованной волне (RHCP). Следующая фигура обеспечивает 3D представление того, на что похожа электромагнитная волна LHCP, когда она перемещается в s - направление.

Когда термины по часовой стрелке или против часовой стрелки используются, они зависят от того, как вы смотрите на волну. Если вы смотрите вдоль направления распространения, то направление по часовой стрелке соответствует поляризации, выполненной правой рукой, и против часовой стрелки соответствует поляризации, выполненной левой рукой. Если вы смотрите на то, куда волна прибывает из, то по часовой стрелке соответствует поляризации, выполненной левой рукой, и против часовой стрелки соответствует поляризации, выполненной правой рукой.

Круговая поляризация, выполненная левой рукой,

Фигура ниже показов внешний вид линейных и циркулярных поляризованных полей, когда они двигают вас вдоль s - направление.

Линейная и круговая поляризация

Эллиптическая поляризация

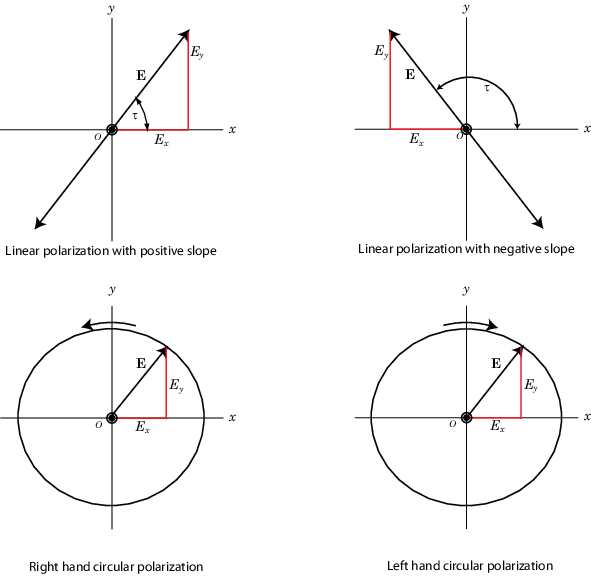
Помимо линейных и круговых состояний поляризации, третий тип поляризации является эллиптической поляризацией. Эллиптическая поляризация включает линейную и круговую поляризацию как особые случаи.

Как с линейной или круговой поляризацией, можно удалить временную зависимость, чтобы получить местоположение точек, что совет вектора электрического поля перемещается

${(\frac{E_{x}}{E_{x 0}})}^{2} + {(\frac{E_{y}}{E_{y 0}})}^{2} - 2 (\frac{E_{x}}{E_{x 0}}) (\frac{E_{y}}{E_{y 0}}) \cos ϕ = \sin^{2} ϕ$

В этом случае, _{φ = φy – φx}. Это уравнение представляет наклоненный двумерный эллипс. Его размер и форма определяются амплитудами компонента и разностью фаз. Присутствие перекрестного термина указывает, что эллипс наклоняется. Уравнение не делает, так же, как в циркулярном поляризованном случае, предоставляет любую информацию о направлении вращения. Например, следующий рисунок показывает мгновенное состояние электрического поля, но не указывает на направление, в котором вращается поле.

Размер и форма двумерного эллипса могут быть заданы тремя параметрами. Эти параметры являются длинами ее двух осей, полуглавной оси, a, и полунезначительной оси, b, и угла наклона, τ. Следующая фигура иллюстрирует три параметра наклоненного эллипса. Можно вывести их из двух амплитуд электрического поля и разности фаз.

Эллипс поляризации

Поляризация может лучше всего быть изучена в терминах комплексных сигналов. Комплексное представление поляризованной волны имеет форму

$E = E_{x 0} e^{i ϕ_{x}} e^{i ω t} {\hat{e}}_{x} + E_{y 0} e^{i ϕ_{y}} e^{i ω t} {\hat{e}}_{y} = (E_{x 0} e^{i ϕ_{x}} {\hat{e}}_{x} + E_{y 0} e^{i ϕ_{y}} {\hat{e}}_{y}) e^{i ω t}$

Задайте комплексный polarization ratio как отношение комплексных амплитуд

$ρ = \frac{E_{y 0}}{E_{x 0}} e^{i (ϕ_{y} - ϕ_{x})} = \frac{E_{y 0}}{E_{x 0}} e^{i ϕ}$

где _{ϕ = ϕy} – _ϕx.

Полезно ввести polarization vector. Поскольку комплекс поляризовал электрическое поле выше, вектор поляризации, P, получен путем нормализации электрического поля

$P = \frac{E_{x 0}}{E_{m}} {\hat{e}}_{x} + \frac{E_{y 0}}{E_{m}} e^{i (ϕ_{y} - ϕ_{x})} {\hat{e}}_{y} = \frac{E_{x 0}}{E_{m}} {\hat{e}}_{x} + \frac{E_{y 0}}{E_{m}} e^{i ϕ} {\hat{e}}_{y}$

где _{Em2 = Ex02 + Ey0} ² является величиной волны.

Полный размер эллипса поляризации не важен, потому что это может варьироваться, когда волна перемещается через пробел, особенно посредством геометрического затухания. То, что важно, является формой эллипса. Таким образом значительные параметры эллипса являются отношением его размерностей оси, a/b, вызвал axial ratio, и tilt angle, τ. Оба из этих количеств могут быть определены из отношения амплитуд компонента и разности фаз, или, эквивалентно, от отношения поляризации. Другим количеством, эквивалентным коэффициенту эллиптичности, является ellipticity angle, ε.

В программном обеспечении Phased Array System Toolbox можно использовать polratio функционируйте, чтобы преобразовать комплексные амплитуды fv=[Ey;Ex] к отношению поляризации.

p = polratio(fv)

Угол наклона

Угол наклона задан как положительное (против часовой стрелки) угол поворота от x - ось к полуглавной оси эллипса. Из-за свойств симметрии эллипса угол наклона, τ, должен только быть заданным в области значений –π/2 ≤ τ ≤ π/2. Можно найти угол наклона путем определения вращаемой системы координат, в которой полуглавные и полунезначительные оси выравниваются с вращаемыми осями координат. Затем уравнение эллипса не имеет никаких перекрестных условий. Решение принимает форму

$\tan 2 τ = \frac{2 E_{x 0} E_{y 0}}{E_{x 0}^{2} - E_{y 0}^{2}} \cos ϕ$

где _{φ = φy – φx}. Заметьте, что можно переписать это уравнение строго в терминах амплитудного отношения и разности фаз.

Коэффициент эллиптичности и угол эллиптичности

После решения для угла наклона можно определить полуглавные и полунезначительные длины оси. Концептуально, вы вращаете эллипс по часовой стрелке углом наклона и измеряете длины пересечений эллипса с x - и y - оси. Точка пересечения с большим значением является полуглавной осью, a, и тот с меньшим значением является полунезначительной осью, b.

Коэффициент эллиптичности задан как AR = a/b и, конструкцией, всегда больше или равен одной. Угол эллиптичности задан

$\tan ε = \mp \frac{b}{a}$

и всегда находится в range–π/4 ≤ τ ≤ π/4.

Если вы задаете вспомогательный угол, α,

$\tan α = \frac{E_{y 0}}{E_{x 0}}$

затем, углом эллиптичности дают

$\sin 2 ε = \sin 2 α \sin ϕ$

И коэффициент эллиптичности и угол эллиптичности заданы от амплитудного отношения и разности фаз и независимы от общей величины поля.

Направление вращения

Для эллиптической поляризации, так же, как с круговой поляризацией, вам нужен другой параметр, чтобы полностью описать эллипс. Этот параметр должен обеспечить направление вращения или направление, которое совет электрического (или магнитный вектор) перемещает вовремя. Скорость изменения угла, который полевой вектор делает с x - ось, является пропорцией к –sin φ, где φ является разностью фаз. Если sin φ положителен, скорость изменения отрицательна, указывая, что поле имеет поляризацию, выполненную левой рукой. Если sin φ отрицателен, скорость изменения является положительной или поляризацией, выполненной правой рукой.

Функция polellip позволяет вам найти значения параметров эллипса поляризации от любого полевым компонентом векторный fv=[Ey;Ex] или отношение поляризации, p.

fv=[Ey;Ex];
[tau,epsilon,ar,rs] = polellip(fv);
p = polratio(fv);
[tau,epsilon,ar,rs] = polellip(p);

Переменные tau\epsilon, ar и rs представляйте угол наклона, угол эллиптичности, коэффициент эллиптичности и направление вращения, соответственно. Оба синтаксиса дают тот же результат.

Сводные данные значения поляризации

Это сводные таблицы несколько различных общих видов поляризации и значения амплитуд, фаз и отношения поляризации, которые производят их:

Поляризация	Амплитуды	Фазы	Отношение поляризации
Линейный положительный наклон	Любые неотрицательные действительные значения для _{Ex, Ey}.	_{φy = φx}	Любое неотрицательное вещественное число
Линейный отрицательный наклон	Любые неотрицательные действительные значения для _{Ex, Ey}	_{φy = φx+ π}	Любое отрицательное вещественное число
Предназначенный для правой руки проспект	_Ex=Ey	_{φy= φx– π/2}	–i
Предназначенный для левой руки проспект	_Ex=Ey	_{φy= φx + π/2}	i
Предназначенный для правой руки эллиптический	Любые неотрицательные действительные значения для _{Ex, Ey}	_{sin (φy– φx) < 0}	sin(arg ρ) < 0
Предназначенный для левой руки эллиптический	Любые неотрицательные действительные значения для _{Ex, Ey}	_{sin (φy– φx) >0}	sin(arg ρ) > 0

Основы линейной и круговой поляризации

Как показано ранее можно описать поляризованное электрическое поле как линейную комбинацию базисных векторов вдоль направлений y и x. Например, комплексные векторы электрического поля для волны предназначенного для правой руки циркулярного поляризованного (RHCP) и волны предназначенного для левой руки циркулярного поляризованного (LHCP), примите форму:

$E = Re [E_{0} (e_{x} \mp i e_{y}) e^{i (ω t + ϕ)}]$

В этом уравнении положительный знак для поля LHCP, и знак минус для поля RHCP. Этим двум специальным комбинациям можно дать новое имя. Задайте новый набор базисного вектора, названный круговым базисным комплектом

$\begin{array}{l} e_{r} = \frac{1}{\sqrt{2}} (e_{x} - i e_{y}) \\ e_{l} = \frac{1}{\sqrt{2}} (e_{x} + i e_{y}) \end{array}$

Можно описать любое поляризованное поле в терминах кругового базисного комплекта вместо линейного базисного комплекта. С другой стороны можно также записать линейное основание поляризации в терминах основания круговой поляризации

$\begin{array}{l} e_{x} & = \frac{1}{\sqrt{2}} (e_{r} + e_{l}) \\ e_{y} & = \frac{1}{\sqrt{2} i} (e_{r} - e_{l}) \end{array}$

Любое общее эллиптическое поле может быть записано как комбинация круговых базисных векторов

$E = E_{l} e_{l} + E_{r} e_{r}$

Вектор Джонса

Поляризованное поле является ортогональным к направлению волны распространения. Таким образом поле может быть полностью задано двумя комплексными компонентами вектора электрического поля в плоскости поляризации. Формулировка поляризованной волны в терминах двухкомпонентных векторов называется формулировкой Jones vector. Формулировка вектора Джонса может быть описана или в линейном основании или в круговом основании или любом основании. Эта таблица показывает представление общей поляризации в линейном основании и круговом основании.

Общая поляризация	Вектор Джонса в линейном основании	Вектор Джонса в круговом основании
Вертикальный	[0;1]	`1/sqrt(2)*[-1;1]`
Горизонталь	[1;0]	`1/sqrt(2)*[1;1]`
Линейные 45 °	`1/sqrt(2)*[1;1]`	`1/sqrt(2)*[1-1i;1+1i]`
Линейные 135 °	`1/sqrt(2)*[1;-1]`	`1/sqrt(2)*[1+1i;1-1i]`
Правильный проспект	`1/sqrt(2)*[1;-1i]`	[0;1]
Оставленный проспект	`1/sqrt(2)*[1;1i]`	[1;0]

Параметры Стокса и сфера Пуанкаре

Эллипс поляризации является мгновенным представлением поляризованной волны. Однако его параметры, угол наклона и угол эллиптичности, часто не непосредственно измеримы, особенно на очень высоких частотах, таких как легкие частоты. Однако можно определить поляризацию из измеримой интенсивности поляризованного поля.

Измеримая интенсивность является параметрами Стокса, _S0, _S1, _S2 и _S3. Первый параметр Стокса, _S0, описывает общую интенсивность поля. Второй параметр, _S1, описывает превосходство линейной горизонтально поляризованной интенсивности по линейной вертикально поляризованной интенсивности. Третий параметр, _S2, описывает превосходство линейно поляризованной интенсивности на +45 ° линейно, 135 ° поляризовали интенсивность. Наконец, _S3 описывает превосходство правильной циркулярной поляризованной интенсивности по левой циркулярной поляризованной интенсивности. Параметры Стокса заданы как

$\begin{array}{l} S_{0} & = E_{x 0}^{2} + E_{y 0}^{2} \\ S_{1} & = E_{x 0}^{2} - E_{y 0}^{2} \\ S_{2} & = 2 E_{x 0} E_{y 0} \cos ϕ \\ S_{3} & = 2 E_{x 0} E_{y 0} \sin ϕ \end{array}$

Для полностью поляризованных полей можно показать усреднением во времени уравнение эллипса поляризации это

$S_{0}^{2} = S_{1}^{2} + S_{2}^{2} + S_{3}^{2}$

Таким образом существуют параметры только трех независимого Стокса.

Для частично поляризованных полей, напротив, параметры Стокса удовлетворяют неравенству

$S_{0}^{2} < S_{1}^{2} + S_{3}^{2} + S_{3}^{2}$

Топит параметры, связаны с наклоном и углами эллиптичности, τ и ε

$\begin{array}{l} S_{1} & = S_{0} \cos 2 τ \cos 2 ε \\ S_{2} & = S_{0} \sin 2 τ \cos 2 ε \\ S_{3} & = S_{0} \sin 2 ε \end{array}$

и обратно пропорционально

$\begin{array}{l} \tan 2 τ & = \frac{S_{2}}{S_{1}} \\ \sin 2 ε & = \frac{S_{3}}{S_{0}} \end{array}$

После того, как вы измерите параметры Стокса, форма эллипса полностью определяется предыдущими уравнениями.

Двумерная сфера Poincaré может помочь вам визуализировать состояние поляризованной волны. Любая точка на или в сфере представляет состояние поляризации, определенной четырьмя параметрами Стокса, _{S0, S1, S2} и _S3. На сфере Poincaré угол от плоскости _S1-S2 до точки на сфере является дважды углом эллиптичности, ε. Угол от оси _S1- до проекции точки в плоскость _S1-S2 является дважды углом наклона, τ.

Как пример, решите для параметров Стокса поля RHCP, fv=[1,-i], использование stokes функция.

S = stokes(fv)

Источники поляризованных полей

Пара антенн, распространяющая электромагнитное излучение к электрическим токам в проводах, электромагнитным полям в волноводах или апертурных полях. Эта связь является явлением, характерным и для передающих и для получающих антенн. Для некоторых передающих антенн, исходных токов в проводном продукте электромагнитные волны, что перенос степени во всех направлениях. Иногда антенна обеспечивает средние значения для ведомой электромагнитной волны на линии электропередачи к переходу к волнам свободного пространства, таким как волновод, питающийся спутниковые антенны. Для получения антенн электромагнитные поля могут побудить токи в проводах генерировать сигналы, которые будут затем усилены и переданы детектору.

Для передающих антенн форма антенны выбрана, чтобы улучшить степень, спроектированную в данное направление. Для получения антенн вы выбираете форму антенны, чтобы улучшить степень, полученную от конкретного направления. Часто, много передающих антенн или антенн получения формируются в array. Массивы увеличивают переданную степень для системы передачи или чувствительность для системы получения. Они улучшают направленность по одной антенне.

Антенна может быть присвоена поляризация. Поляризация передающей антенны является поляризацией своей излученной волны в далеком поле. Поляризация антенны получения является на самом деле поляризацией плоской волны, от данного направления, приводящего к максимальной мощности на терминалах антенны. Теоремой взаимности все передающие антенны могут служить получением антенн и наоборот.

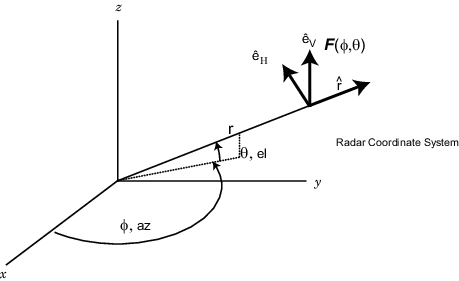
Каждая антенна или массив имеют связанную локальную Декартову систему координат (x,y,z) как показано в следующем рисунке. Смотрите Системы Глобальной и Локальной координаты для получения дополнительной информации. Система локальной координаты может также быть представлена сферической системой координат с помощью азимута, вертикального изменения и координат области значений, az, el, r, или альтернативно писаться, (φ,θ,r), как показано. В каждой точке в далеком поле можно создать набор модульных векторов сферического базиса, ${{\hat{e}}_{H}, {\hat{e}}_{V}, \hat{r}}$ . Базисные векторы выравниваются с направлениями (φ,θ,r), соответственно. В далеком поле электрическое поле является ортогональным к единичному вектору $\hat{r}$ . Компоненты поляризованного поля относительно этого основания, _(EH,EV), называются горизонтальными и вертикальными составляющими поляризованного поля. В радаре распространено использовать (H,V) вместо (x,y), чтобы обозначить компоненты поляризованного поля. В далеком поле поляризованное электрическое поле принимает форму

$E = F (ϕ, θ) \frac{e^{i k r}}{r} = (F_{H} (ϕ, θ) {\hat{e}}_{H} + F_{V} (ϕ, θ) {\hat{e}}_{V}) \frac{e^{i k r}}{r}$

В этом уравнении количество F (φ,θ) называется vector radiation pattern источника и содержит угловую зависимость поля в области далекого поля.

Короткий дипольный антенный элемент

Самая простая поляризованная антенна является дипольной антенной, которые состоят из длины разделения провода, связанного в середину с коаксиальным кабелем. Самый простой диполь, с математической точки зрения, является диполем Hertzian, в котором длина провода намного короче, чем длина волны. Схема короткой дипольной антенны длины L появляется на следующем рисунке. Эта антенна питается коаксиальным каналом, который разделяет в два провода равной длины длины L/2. Ток, I, проходит z - ось и принят, чтобы быть тем же самым во всех точках в проводе.

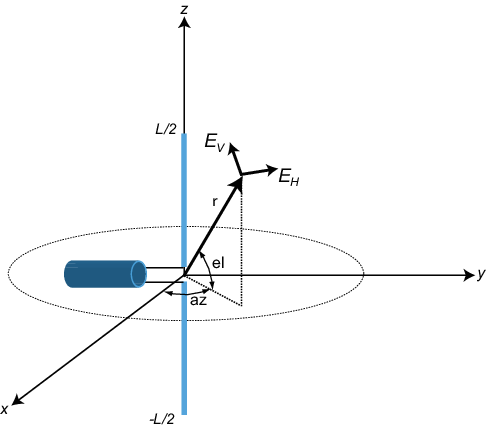
Электрическое поле в далеком поле имеет форму

$\begin{array}{l} E_{r} = 0 \\ E_{H} = 0 \\ E_{V} = - \frac{i Z_{0} I L}{2 λ} \cos el \frac{e^{- i k r}}{r} \end{array}$

Следующий пример вычисляет вертикальные и горизонтальные компоненты поляризации поля. Вертикальная составляющая является функцией угла возвышения и по оси симметрична. Горизонтальная составляющая исчезает везде.

Тулбокс позволяет вам смоделировать короткую дипольную антенну с помощью phased.ShortDipoleAntennaElement Система object™.

Компоненты поляризации короткого диполя

Скрипт Open Live Script

Вычислите вертикальные и горизонтальные компоненты поляризации поля, созданного антенной короткого диполя, указанной вдоль z-направления. Постройте компоненты как функцию угла возвышения от 0 ° до 360 °.

Примечание: Этот пример запускается только в R2016b или позже. Если вы используете более ранний релиз, заменяете каждый вызов функции с эквивалентным step синтаксис. Например, замените myObject(x) с step(myObject,x).

Создайте phased.ShortDipoleAntennaElement Система object™.

antenna = phased.ShortDipoleAntennaElement(...
    'FrequencyRange',[1,2]*1e9,'AxisDirection','Z');

Вычислите ответ антенны. Поскольку аргумент угла возвышения к antenna ограничивается ±90 °, вычислите ответы для азимута на 0 ° и затем для азимута на 180 °. Объедините эти два ответа в графике. Рабочая частота антенны составляет 1,5 ГГц.

el = [-90:90];
az = zeros(size(el));
fc = 1.5e9;
resp = antenna(fc,[az;el]);
az = 180.0*ones(size(el));
resp1 = antenna(fc,[az;el]);

Наложите ответы на том же рисунке.

figure(1)
subplot(121)
polar(el*pi/180.0,abs(resp.V.'),'b')
hold on
polar((el+180)*pi/180.0,abs(resp1.V.'),'b')
str = sprintf('%s\n%s','Vertical Polarization','vs Elevation Angle');
title(str)
hold off
subplot(122)
polar(el*pi/180.0,abs(resp.H.'),'b')
hold on
polar((el+180)*pi/180.0,abs(resp1.H.'),'b')
str = sprintf('%s\n%s','Horizontal Polarization','vs Elevation Angle');
title(str)
hold off

График показывает, что горизонтальная составляющая исчезает, как ожидалось.

Пересеченный дипольный антенный элемент

Можно использовать перекрестную дипольную антенну, чтобы сгенерировать циркулярно поляризованное излучение. Антенна пересеченного диполя состоит из двух идентичных, но ортогональных антенн короткого диполя, которые поэтапно осуществлены на расстоянии в 90 °. Схема пересеченной дипольной антенны появляется в следующем рисунке. Электрическое поле, созданное антенной пересеченного диполя, созданной из y - направило короткий диполь, и z - предписал, чтобы короткий диполь имел форму

$\begin{array}{l} E_{r} = 0 \\ E_{H} = - \frac{i Z_{0} I L}{2 λ} \cos азимут \frac{e^{- i k r}}{r} \\ E_{V} = \frac{i Z_{0} I L}{2 λ} (\sin el \sin азимут + i \cos el) \frac{e^{- i k r}}{r} \end{array}$

_EV/EH отношения поляризации, когда оценено вдоль x - ось, является только –i, что означает, что поляризацией является точно RHCP вдоль x - ось. Это - преимущественно RHCP, когда наблюдательный пост близко к x - ось. Переезжая от x - ось, поле становится смесью LHCP и поляризации RHCP. Вдоль –x - ось, поле является поляризованным LHCP. Фигура иллюстрирует для точки около x, что полем является, в основном, RHCP.

Тулбокс позволяет вам смоделировать антенну пересеченного диполя с помощью phased.CrossedDipoleAntennaElement Системный объект.

LHCP и компоненты поляризации RHCP

Скрипт Open Live Script

Этот пример строит правые и левые компоненты круговой поляризации полей, сгенерированных антенной пересеченного диполя на уровне 1,5 ГГц. Вы видите, как круговая поляризация изменяется от чистого RHCP под 0 углами азимута степеней к чистому LHCP под 180 углами азимута степеней, обоим в 0 углах возвышения степеней.

Создайте phased.CrossedDipoleAntennaElement объект.

fc = 1.5e9;
antenna = phased.CrossedDipoleAntennaElement('FrequencyRange',[1,2]*1e9);

Вычислите предназначенные для левой руки и предназначенные для правой руки компоненты круговой поляризации из ответа антенны.

az = [-180:180];
el = zeros(size(az));
resp = antenna(fc,[az;el]);
cfv = pol2circpol([resp.H.';resp.V.']);
clhp = cfv(1,:);
crhp = cfv(2,:);

Постройте оба компонента круговой поляризации при 0 вертикальных изменениях степеней.

polar(az*pi/180.0,abs(clhp))
hold on
polar(az*pi/180.0,abs(crhp))
title('LHCP and RHCP vs Azithmuth Angle')
legend('LHCP','RHCP')
hold off

Массивы, поддерживающие поляризацию

Можно создать поляризованные поля из массивов при помощи поляризованных антенных элементов как значение Elements свойство Системного объекта массивов. Все массивы Phased Array System Toolbox поддерживают поляризацию.

Матрица поперечного сечения рассеяния

После того, как поляризованное поле создается системой антенны, поле исходит в область далекого поля. Когда поле распространяет в свободное пространство, свойства поляризации остаются неизменными, пока поле не взаимодействует с материальным веществом, которое рассеивает поле во многие направления. В таких ситуациях амплитуда и поляризация рассеянной волны могут отличаться от инцидентной поляризации волны. Рассеянная поляризация волны может зависеть от направления, в котором наблюдается рассеянная волна. Точный способ, которым изменения поляризации зависят от свойств рассеивающегося объекта. Количество, описывающее ответ объекта к падающему полю, называется радарной матрицей поперечного сечения рассеяния (RSCM), S. Можно измерить матрицу рассеяния можно следующим образом. Когда модульная амплитуда, горизонтально поляризованная волна рассеивается, и горизонталь и вертикальный рассеянный компонент, производится. Вызовите эти два компонента _SHH и _SVH. Эти компоненты являются комплексными числами, содержащими амплитуду и фазовые переходы от инцидентной волны. Точно так же, когда модульной амплитудой, вертикально поляризованная волна рассеивается, горизонталь и вертикальный рассеянный произведенный компонент, является _SHV и _SVV. Поскольку, любое падающее поле может быть разложено на горизонтальные и вертикальные составляющие, можно расположить эти количества в матрицу и записать рассеянное поле в терминах падающего поля

$[\begin{matrix} E_{H}^{(s c a t)} \\ E_{V}^{(s c a t)} \end{matrix}] = \sqrt{\frac{4 π}{λ^{2}}} [\begin{matrix} S_{H H} & S_{V H} \\ S_{H V} & S_{V V} \end{matrix}] [\begin{matrix} E_{H}^{(i n c)} \\ E_{V}^{(i n c)} \end{matrix}] = \sqrt{\frac{4 π}{λ^{2}}} [S] [\begin{matrix} E_{H}^{(i n c)} \\ E_{V}^{(i n c)} \end{matrix}]$

В общем случае матрица поперечного сечения рассеяния зависит от углов, которые падающие и рассеянные поля делают с объектом. Когда падающее поле рассеивается назад к передающей антенне или, backscattered, матрица рассеяния симметрична.

Сигнатура поляризации

Чтобы понять, как рассеянная волна зависит от поляризации падающей волны, необходимо изучить все возможные поляризации рассеянного поля для каждой падающей поляризации. Поскольку этот объем данных затрудняет, чтобы визуализировать, рассмотрите два случая:

Для случая copolarization рассеянная поляризация имеет ту же поляризацию как падающее поле.
Для случая cross-polarization рассеянная поляризация имеет ортогональную поляризацию к падающему полю.

Можно представлять падающие поляризации в терминах пары угла наклона-угла эллиптичности $(τ, ε)$ . Каждый единичный падающий вектор поляризации может быть описан как

$[\begin{matrix} E_{H}^{(i n c)} \\ E_{V}^{(i n c)} \end{matrix}] = [\begin{matrix} \cos τ & - \sin τ \\ \sin τ & \cos τ \end{matrix}] [\begin{matrix} \cos ε \\ j \sin ε \end{matrix}]$

в то время как ортогональный вектор поляризации

$[\begin{matrix} E_{H}^{(i n c) ⊥} \\ E_{V}^{(i n c) ⊥} \end{matrix}] = [\begin{matrix} - \sin τ & - \cos τ \\ \cos τ & - \sin τ \end{matrix}] [\begin{matrix} \cos ε \\ - j \sin ε \end{matrix}]$

Когда вы имеете матрицу RSCM, S, формируете сигнатуру сополяризации путем вычисления

$P^{(c o)} = {[\begin{matrix} E_{H}^{(i n c)} & E_{V}^{(i n c)} \end{matrix}]}^{*} S [\begin{matrix} E_{H}^{(i n c)} \\ E_{V}^{(i n c)} \end{matrix}]$

где []* обозначает комплексное спряжение. Чтобы получить подпись перекрестной поляризации, вычислить

$P^{(c r o s s)} = {[\begin{matrix} E_{H}^{(i n c) ⊥} & E_{V}^{(i n c) ⊥} \end{matrix}]}^{*} S [\begin{matrix} E_{H}^{(i n c)} \\ E_{V}^{(i n c)} \end{matrix}]$

Можно вычислить как сигнатуры сополяризации, так и сигнатуры перекрестной поляризации, с помощью polsignature функция. Эта функция возвращает абсолютное значение рассеянной мощности (нормированный на ее максимальное значение). Следующий пример показывает, как построить сигнатуры поляризации для матрицы RSCM

$S = [\begin{matrix} 2 i & \frac{1}{2} \\ \frac{1}{2} & i \end{matrix}]$

для всех возможных падающих поляризаций. Диапазон значений угла эллиптичности и наклона охватывает весь возможный диапазон поляризаций.

Построение Поляризационных Сигнатур

Скрипт Open Live Script

Построение сигнатур сополяризации и кросс-поляризации матрицы рассеяния

$[\begin{array}{cc} 2 i & 0.5 \\ 0.5 & - i \end{array}] .$

Задайте матрицу рассеяния. и укажите диапазон углов эллиптичности и ориентации (наклон) углы, которые задают виды поляризации. Эти углы покрывают все возможные состояния падающей поляризации.

rscmat = [1i*2,0.5;0.5,-1i];
el = [-45:45];
tilt = [-90:90];

Постройте сигнатуры сополяризации для всех падающих поляризаций.

polsignature(rscmat,'c',el,tilt)

Постройте подписи перекрестной поляризации для всех падающих поляризаций.

polsignature(rscmat,'x',el,tilt)

Потеря поляризации из-за несоответствия поля и приемника

Антенна, которая используется для приема поляризованных электромагнитных волн, достигает своей максимальной выходной мощности, когда поляризация антенны согласована с поляризацией падающего электромагнитного поля. В противном случае происходит потеря поляризации:

Потеря поляризации вычисляется из проекции (или скалярное произведение) вектора электрического поля переданного поля на вектор поляризации приемника.
Потеря происходит, когда существует несоответствие в направлении этих двух векторов, не в их величинах.
Коэффициент потерь поляризации описывает долю падающей мощности, которая имеет правильную поляризацию для приема.

Используя сферический базис передатчика в положении приемника, можно представлять падающее электрическое поле, _{(EiH, EiV)},

$E = E_{i H} {\hat{e}}_{H} + E_{i V} {\hat{e}}_{V} = E_{m} P_{i}$

Можно представлять вектор поляризации приемника, _{(PH, PV)}, в локальном сферическом базисе приемника:

$P = P_{H} {\hat{e}}^{'}_{H} + P_{V} {\hat{e}}^{'}_{V}$

Следующий рисунок показывает конструкцию векторов сферического базиса передатчика и приемника.

Потеря поляризации задана:

$ρ = \frac{| E_{i} \cdot P |^{2}}{| E_{i} |^{2} | P |^{2}}$

и находится в интервале между 0 и 1. Поскольку векторы заданы относительно различных систем координат, они должны быть преобразованы в глобальную систему координат, чтобы сформировать проекцию. Функция тулбокса polloss вычисляет несоответствие поляризации между падающим полем и поляризованной антенной.

Чтобы достигнуть максимальной выходной мощности от антенны получения, совпадающий вектор поляризации антенны должен быть сопряженным комплексным числом вектора поляризации входящего поля. Как пример, если входящее поле является RHCP с вектором поляризации, данным $e_{r} = \frac{1}{\sqrt{2}} (e_{x} - i e_{y})$ , оптимальная поляризация антенны приемника является LHCP. В представлении сопряженного комплексного числа нуждаются, потому что полевая поляризация описана относительно его направления распространения, тогда как поляризация получить антенны обычно задается в терминах направления распространения к антенне. Сопряженное комплексное число корректирует для противоположного смысла поляризации при получении.

Как пример, если передающая антенна передает поле RHCP, коэффициенты потерь поляризации для различной полученной поляризации антенны

Получите поляризацию антенны	Получите вектор поляризации антенны	Коэффициент потерь поляризации	Коэффициент потерь поляризации (дБ)
Линейная горизонталь	e _H	1/2	3 дБ
Вертикальный линейный	e _V	1/2	3
RHCP	$e_{r} = \frac{1}{\sqrt{2}} (e_{x} - i e_{y})$	0	∞
LHCP	$e_{l} = \frac{1}{\sqrt{2}} (e_{x} + i e_{y})$	1	0

Радар модели, передающий поляризованное излучение

Скрипт Open Live Script

Этот пример демонстрирует радар отслеживания на основе 31 31 универсального прямоугольного массива (URA) (с 961 элементом). Радар спроектирован, чтобы следовать за движущейся целью. В каждый раз момент радар указывает в известном направлении цели. Основные радарные требования являются вероятностью обнаружения, pd, вероятность ложного предупреждения, pfa, максимальная однозначная область значений, max_range, и разрешение области значений, range_res, (все единицы расстояния исчисляются в метрах). range_gate параметр ограничивает необходимую область областью значений, меньшей, чем максимальная область значений. Рабочая частота установлена в fc. Симуляция длится numpulses импульсы.

Радарное определение

Настройте радарные рабочие параметры. Существующий радарный проект выполняет следующим техническим требованиям.

pd = 0.9;            % Probability of detection
pfa = 1e-6;          % Probability of false alarm
max_range = 1500*1000; % Maximum unambiguous range
range_res = 50.0;    % Range resolution
rangegate = 5*1000;  % Assume all objects are in this range
numpulses = 200;     % Number of pulses to integrate
fc = 8e9;            % Center frequency of pulse
c = physconst('LightSpeed');
tmax = 2*rangegate/c; % Time of  echo from object at rangegate

Импульсный интервал повторения

Установите импульсный интервал повторения, PRI, и импульсная частота повторения, PRF, на основе максимальной однозначной области значений.

PRI = 2*max_range/c;
PRF = 1/PRI;

Переданный сигнал

Настройте передаваемую прямоугольную форму сигнала с помощью phased.RectangularWaveform System object(TM). Ширина импульса формы волны, pulse_width, и ширина полосы пропускания импульса, pulse_bw, определяются разрешением области значений, range_res, который вы выбираете. Задайте частоту дискретизации, fs, быть дважды шириной полосы пропускания импульса. Частота дискретизации должна быть целочисленным кратным PRF. Поэтому измените частоту дискретизации, чтобы удовлетворить требованию.

pulse_bw = c/(2*range_res);    % Pulse bandwidth
pulse_width = 1/pulse_bw;               % Pulse width
fs = 2*pulse_bw;                        % Sampling rate
n = ceil(fs/PRF);
fs = n*PRF;
waveform = phased.RectangularWaveform('PulseWidth',pulse_width,'PRF',PRF,...
    'SampleRate',fs);

Антенны и массив URA

Массив состоит из антенных элементов короткого диполя. Используйте phased.ShortDipoleAntennaElement Системный объект, чтобы создать антенну короткого диполя, ориентированную вдоль оси z.

antenna = phased.ShortDipoleAntennaElement(...
    'FrequencyRange',[5e9,10e9],'AxisDirection','Z');

Задайте 31 31, Тейлор заострился универсальный прямоугольный массив с помощью phased.URA Системный объект. Установите размер массива с помощью количества строк, numRows, и количество столбцов, numCols. Расстояние между элементами, d, немного меньше, чем половина длины волны, lambda. Вычислите заострение массивов, tw, использование отдельных окон Тейлора для направлений строки и столбца. Получите веса Тейлора с помощью taylorwin функция. Постройте ответ трехмерного массива с помощью массива pattern метод.

numCols = 31;
numRows = 31;
lambda = c/fc;
d = 0.9*lambda/2; % Nominal spacing
wc = taylorwin(numCols);
wr = taylorwin(numRows);
tw = wr*wc';
array = phased.URA('Element',antenna,'Size',[numCols,numRows],...
    'ElementSpacing',[d,d],'Taper',tw);
pattern(array,fc,[-180:180],[-90:90],'CoordinateSystem','polar','Type','powerdb',...
    'Polarization','V');

Радарное движение платформы

Затем установите положение и движение радарной платформы в phased.Platform Системный объект. Радар принят, чтобы быть стационарным и расположен в источник. Установите Velocity свойство к [0,0,0] и InitialPosition свойство к [0,0,0]. Установите InitialOrientationAxes свойство к единичной матрице, чтобы выровнять радарные оси координат платформы с глобальной системой координат.

radarPlatformAxes = [1 0 0;0 1 0;0 0 1];
radarplatform = phased.Platform('InitialPosition',[0;0;0],...
    'Velocity',[0;0;0],'OrientationAxes',radarPlatformAxes);

Передатчики и приемники

В радаре сигнал распространяет в форме электромагнитной волны. Сигнал излучен и собран антеннами, используемыми в радиолокационной системе. Сопоставьте массив с Системным объектом теплоотвода, phased.Radiator, и два коллектора System objects, phased.Collector. Установите WeightsInputPort свойство теплоотвода к true включить динамическое регулирование переданного сигнала при каждом выполнении теплоотвода. Создание этих двух коллекторов допускает набор и горизонтальных и вертикальных компонентов поляризации.

radiator = phased.Radiator('Sensor',array,'OperatingFrequency',fc,...
    'PropagationSpeed',c,'CombineRadiatedSignals',true,...
    'Polarization','Combined','WeightsInputPort',true);
collector1 = phased.Collector('Sensor',array,'OperatingFrequency',fc,...
    'PropagationSpeed',c,'Wavefront','Plane','Polarization','Combined',...
    'WeightsInputPort',false);
collector2 = phased.Collector('Sensor',array,'OperatingFrequency',fc,...
    'PropagationSpeed',c,'Wavefront','Plane','Polarization','Combined',...
    'WeightsInputPort',false);

Оцените пиковую мощность, необходимую в phased.Transmitter Системный объект, чтобы вычислить желаемые излученные уровни мощности. Переданная пиковая мощность является степенью, требуемой достигнуть ОСШ минимального обнаружения, snr_min. Можно определить минимальный ОСШ из вероятности обнаружения, |pd |, и вероятности ложного предупреждения, pfa, использование albersheim функция. Затем вычислите пиковую мощность из основного уравнения радиолокации с помощью radareqpow функция. Среди входных параметров к этой функции полное усиление сигнала, которое является суммой усиления элемента передачи, TransmitterGain и усиление массивов, AG. Другой вход является максимальной областью значений обнаружения, rangegate. Наконец, необходимо предоставить эффективную площадь рассеяния цели, tgt_rcs. Скалярное поперечное сечение радара используется в этой секции кода в качестве приближения даже при том, что полное вычисление поляризации более позднее использование матрица рассеяния поперечного сечения радара 2 на 2.

Оцените общую переданную степень достигнуть необходимого ОСШ обнаружения с помощью всех импульсов.

ОСШ имеет вклады от усиления элемента передачи, а также усиления массивов. Вычислите сначала оценку усиления массивов, затем добавьте усиление массивов в усиление передатчика, чтобы получить пиковую мощность, которая достигает желаемого ОСШ.

Используйте аппроксимированное целевое сечение 1,0 для основного уравнения радиолокации даже при том, что анализ призывает к полной матрице рассеяния.
Установите максимальную область значений быть равной значению 'rangegate', поскольку цели вне той области значений неинтересны.
Вычислите усиление массивов как 10*log10 (число элементов)
Примите, что каждый элемент имеет усиление 20 дБ.

snr_min = albersheim(pd, pfa, numpulses);
AG = 10*log10(numCols*numRows);
tgt_rcs = 1;
TransmitterGain = 20;
peak_power = radareqpow(lambda,rangegate,snr_min,waveform.PulseWidth,...
    'RCS',tgt_rcs,'Gain',TransmitterGain + AG);
transmitter = phased.Transmitter('PeakPower',peak_power,'Gain',TransmitterGain,...
    'LossFactor',0,'InUseOutputPort',true,'CoherentOnTransmit',true);

Задайте цель

Мы хотим симулировать импульс, возвращается из цели, которая вращается так, чтобы матрица поперечного сечения рассеяния изменилась от импульса до импульса. Создайте вращающийся целевой объект и движущуюся целевую платформу. Вращающаяся цель представлена позже как зависимая углом матрица рассеяния. Вращение в градусах в секунду.

targetSpeed = 1000;
targetVec = [-1;1;0]/sqrt(2);
target = phased.RadarTarget('EnablePolarization',true,...
    'Mode','Monostatic','ScatteringMatrixSource','Input port',...
    'OperatingFrequency',fc);
targetPlatformAxes = [1 0 0;0 1 0;0 0 1];
targetRotRate = 45;
targetplatform = phased.Platform('InitialPosition',[3500.0; 0; 0],...
    'Velocity', targetSpeed*targetVec);

Другие Системные объекты

Регулирование вектора задано phased.SteeringVector Системный объект.
Формирователь луча задан phased.PhaseShiftBeamformer Системный объект. DirectionSource свойство установлено в 'Input Port' включить формирователь луча к всегда точкам к известному целевому направлению при каждом выполнении.
Распространитель свободного пространства, использующий phased.FreeSpace Системный объект.
Модель предусилителя приемника использование phased.ReceiverPreamp системный объект.

Распространение сигнала

Поскольку отраженные сигналы получены массивом, используйте формирователь луча, указывающий на держащееся направление, чтобы получить объединенный сигнал.

steeringvector = phased.SteeringVector('SensorArray',array,'PropagationSpeed',c,...
    'IncludeElementResponse',false);
beamformer = phased.PhaseShiftBeamformer('SensorArray',array,...
    'OperatingFrequency',fc,'PropagationSpeed',c,...
    'DirectionSource','Input port');
channel = phased.FreeSpace('SampleRate',fs,...
    'TwoWayPropagation',true,'OperatingFrequency',fc);
% Define a receiver with receiver noise
amplifier = phased.ReceiverPreamp('Gain',20,'LossFactor',0,'NoiseFigure',1,...
    'ReferenceTemperature',290,'SampleRate',fs,'EnableInputPort',true,...
    'PhaseNoiseInputPort',false,'SeedSource','Auto');

Для такого большого PRI и частоты дискретизации, будет слишком много выборок на элемент. Это вызовет проблемы с коллектором, который имеет 961 канал. Чтобы сохранить количество выборок управляемым, установите максимальную область значений 5 км. Мы знаем, что цель в этой области значений.

Этот набор осей задает направление осей локальной координаты относительно глобальной системы координат. Это - ориентация цели.

Обработка цикла

Предварительно выделите массивы для сбора данных, которые будут построены.

sig_max_V  = zeros(1,numpulses);
sig_max_H  = zeros(1,numpulses);
tm_V = zeros(1,numpulses);
tm_H = zeros(1,numpulses);

После того, как все Системные объекты создаются, цикл по количеству импульсов, чтобы создать отраженные сигналы.

maxsamp = ceil(tmax*fs);
fast_time_grid = [0:(maxsamp-1)]/fs;
rotangle = 0.0;
for m = 1:numpulses
    x = waveform(); % Generate pulse
    % Capture only samples within range gated
    x = x(1:maxsamp);
    [s, tx_status] = transmitter(x);   % Create transmitted pulse
    % Move the radar platform and target platform.
    [radarPos,radarVel] = radarplatform(1/PRF);
    [targetPos,targetVel] = targetplatform(1/PRF);    
    % Compute the known target angle
    [targetRng,targetAng] = rangeangle(targetPos,...
        radarPos,...
        radarPlatformAxes);
    % Compute the radar angle with respect to the target axes.
    [radarRng,radarAng] = rangeangle(radarPos,...
        targetPos,...
        targetPlatformAxes);    
    % Calculate the steering vector designed to track the target
    sv = steeringvector(fc,targetAng);
    % Radiate the polarized signal toward the targat
    tsig1 = radiator(s,targetAng,radarPlatformAxes,conj(sv));
    % Compute the two-way propagation loss (4*pi*R/lambda)^2
    tsig2 = channel(tsig1,radarPos,targetPos,radarVel,targetVel);
    % Create a very simple model of a changing scattering matrix
    scatteringMatrix = [cosd(rotangle),0.5*sind(rotangle);...
        0.5*sind(rotangle),cosd(rotangle)];
    rsig1 = target(tsig2,radarAng,targetPlatformAxes,scatteringMatrix);  % Reflect off target
    % Collect the vertical component of the radiation.
    rsig3V = collector1(rsig1,targetAng,radarPlatformAxes);   
    % Collect the horizontal component of the radiation. This
    % second collector is rotated around the x-axis to be more
    % sensitive to horizontal polarization
    rsig3H = collector2(rsig1,targetAng,rotx(90)*radarPlatformAxes);  
    % Add receiver noise to both sets of signals
    rsig4V = amplifier(rsig3V,~(tx_status>0)); % Receive signal
    rsig4H = amplifier(rsig3H,~(tx_status>0)); % Receive signal
    % Beamform the signal
    rsigV = beamformer(rsig4V,targetAng); % Beamforming
    rsigH = beamformer(rsig4H,targetAng); % Beamforming   
    % Find the maximum returns for each pulse and store them in
    % a vector. Store the pulse received time as well.
    [sigmaxV,imaxV] = max(abs(rsigV));
    [sigmaxH,imaxH] = max(abs(rsigH));
    sig_max_V(m) = sigmaxV;
    sig_max_H(m) = sigmaxH;
    tm_V(m) = fast_time_grid(imaxV) + (m-1)*PRI;
    tm_H(m) = fast_time_grid(imaxH) + (m-1)*PRI;
    
    % Update the orientation of the target platform axes
    targetPlatformAxes = ...
        rotx(PRI*targetRotRate)*targetPlatformAxes;
    rotangle = rotangle + PRI*targetRotRate;
end
% Plot the vertical and horizontal polarization for each pulse as a
% function of time.
plot(tm_V,sig_max_V,'.')
hold on
plot(tm_H,sig_max_H,'r.')
hold off
xlabel('Time (sec)')
ylabel('Amplitude')
title('Vertical and Horizontal Polarization Components')
legend('Vertical','Horizontal')
grid on

Документация