Формирование цикла смешанной чувствительности

Формирование цикла смешанной чувствительности позволяет вам спроектировать H _∞ контроллер путем одновременного формирования частотных характеристик для отслеживания и подавления помех, шумоподавления и робастности и усилия контроллера. Этот метод является полезным способом сбалансировать необходимый компромисс между эффективностью и робастностью. Чтобы использовать этот метод, вы преобразуете свои желаемые ответы максимум в три функции взвешивания что mixsyn использование команды, чтобы синтезировать контроллер.

Setup задач

mixsyn проектирует контроллер K для вашего объекта G, принимая стандартную настройку управления следующей схемы.

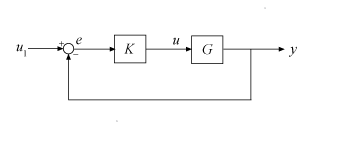
Для этого функция добавляет функции взвешивания, которые вы обеспечиваете, W ₁ (s), W ₂ (s) и W ₃ (s), к системе управления, как показано в следующей схеме.

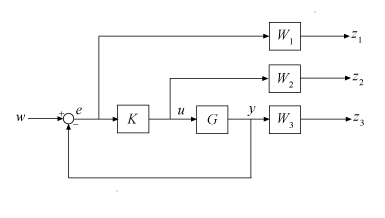
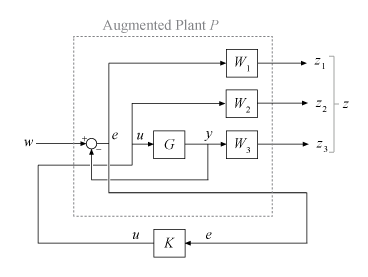
mixsyn обрабатывает проблему как H _∞ проблема синтеза (см. hinfsyn). Это анализирует взвешенную систему управления как LFT (P, K), где P является увеличенным объектом P, таким образом что {z; e} = P {w; u}, как показано в следующей схеме.

Передаточная функция от w до z может быть описана как

$M (s) = [\begin{matrix} W_{1} S \\ W_{2} K S \\ W_{3} T \end{matrix}],$

где

S = (I + GK) ^–1 является функцией чувствительности.
KS является передаточной функцией от w до u (усилие по управлению).
T = (I – S) = GK (I + GK) ^–1 является дополнительной функцией чувствительности.

mixsyn ищет контроллер K, который минимизирует || M (s) || _∞, H _∞ норма (пиковое усиление) M. Для этого это вызывает hinfsyn на увеличенном объекте P = augw(G,W1,W2,W3).

Выберите Weighting Functions

Усиление цикла for L = GK, чтобы достигнуть хорошего отслеживания уставки и подавления помех, вы обычно хотите высокое усиление цикла в низкой частоте. Чтобы достигнуть робастности и затухания шума измерения, вы обычно хотите, чтобы L прокрутился прочь на высокой частоте. Эта форма цикла эквивалентна маленькому S в низкой частоте и маленькому T на высокой частоте.

Для формирования цикла смешанной чувствительности вы выбираете функции взвешивания, чтобы задать те целевые формы для S и T, а также усилия по управлению KS. H _∞ конструктивное ограничение,

${‖ M (s) ‖}_{\infty} = {‖ [\begin{matrix} W_{1} S \\ W_{2} K S \\ W_{3} T \end{matrix}] ‖}_{\infty} \leq 1,$

средние значения это

$\begin{matrix} {‖ S ‖}_{\infty} \leq | W_{1}^{- 1} | \\ {‖ K S ‖}_{\infty} \leq | W_{2}^{- 1} | \\ {‖ T ‖}_{\infty} \leq | W_{3}^{- 1} | . \end{matrix}$

Поэтому вы устанавливаете веса, равные обратным величинам желаемых форм для S, KS и T. В частности,

Для хорошего отслеживания уставки и эффективности подавления помех, выберите W₁, большой в пропускной способности управления, чтобы получить маленький S.
Для робастности и шумового затухания, выберите W₃, большой вне пропускной способности управления, чтобы получить маленький T.
Чтобы ограничить усилие по управлению в конкретном диапазоне частот, увеличьте величину W ₂ в этом диапазоне частот, чтобы получить маленький KS.

mixsyn возвращает минимум || M (s) || _∞ в выходном аргументе gamma. Для возвращенного контроллера K, затем,

$\begin{matrix} {‖ S ‖}_{\infty} \leq γ | W_{1}^{- 1} | \\ {‖ K S ‖}_{\infty} \leq γ | W_{2}^{- 1} | \\ {‖ T ‖}_{\infty} \leq γ | W_{3}^{- 1} | . \end{matrix}$

Если вы не хотите ограничивать усилие по управлению, можно не использовать W ₂. В этом случае, mixsyn минимизирует H _∞ норма

$M (s) = [\begin{matrix} W_{1} S \\ W_{3} T \end{matrix}] .$

Можно использовать makeweight создать функции взвешивания с желаемыми профилями усиления. Следующий пример иллюстрирует, как выбрать и создать функции взвешивания для проектирования контроллера с mixsyn.

Числовые факторы

Не выбирайте функции взвешивания с полюсами очень близко к s = 0 (z = 1 для систем дискретного времени). Например, несмотря на то, что может казаться разумным выбрать W₁ = 1/s, чтобы осуществить нулевую установившуюся ошибку, делание так вводит нестабильный полюс, который не может быть стабилизирован, заставив синтез перестать работать. Вместо этого выберите W₁ = 1 / (s + δ). Значение δ должно быть малым, но не очень маленькое по сравнению с системной динамикой. Например, для лучших числовых результатов, если ваша целевая частота среза составляет приблизительно 1 рад/с, выбирают δ = 0.0001 или 0.001. Точно так же в дискретное время, выберите шаги расчета, таким образом, что система и динамика взвешивания составляют не больше чем десятилетие или два ниже частоты Найквиста.

Проектирование контроллера формирования цикла смешанной чувствительности

Скрипт Open Live Script

Загрузите модель объекта управления для смешанной чувствительности $H_{\infty}$ проектирование контроллера. Этот 2D вход, 2D выход, модель с шестью состояниями описана в Формировании Цикла в качестве примера Контроллера Оси Подачи HIMAT.

load mixsynExampleData G
size(G)

State-space model with 2 outputs, 2 inputs, and 6 states.

Чтобы спроектировать контроллер для эффективности и робастности, сформируйте чувствительность и дополнительные функции чувствительности. Выберите веса, которые являются инверсией желаемых форм.

Чтобы достигнуть хорошего отслеживания уставки и эффективности подавления помех, сформируйте S, чтобы быть малыми в пропускной способности управления, что означает выбор W1 большой в низкой частоте, прокручивающейся прочь на высокой частоте. В данном примере задайте W1 с:

Низкочастотное усиление приблизительно 30 дБ (33 в абсолютных единицах)
Высокочастотное усиление приблизительно-6 дБ (0.5 в абсолютных единицах)
Перекрестное соединение на 0 дБ на уровне приблизительно 5 рад/с.

W1 = makeweight(33,5,0.5);

Для робастности и шумового затухания, сформируйте T быть малыми вне пропускной способности управления, что означает выбор W3 большой на высокой частоте.

W3 = makeweight(0.5,20,20);

Исследуйте обе функции взвешивания. Их инверсии являются целевыми формами для S и T.

bodemag(W1,W3)
yline(0,'--');
legend('W1','W3','0 dB')
grid on

Поскольку S + T = I, mixsyn не может сделать оба S и T маленький (меньше чем 0 дБ) в том же частотном диапазоне. Поэтому, когда вы задаете веса, должен быть диапазон частот в который оба W1 и W3 ниже 0 дБ.

Используйте mixsyn вычислять оптимальный контроллер смешанной чувствительности с этими весами. В данном примере не наложите штраф на усилие контроллера установки W2 к [].

[K,CL,gamma] = mixsyn(G,W1,[],W3);
gamma

gamma = 0.7331

Получившийся gamma, то, которое является пиковым сингулярным значением через все частоты, значительно ниже 1, указывая, что система с обратной связью соответствует конструктивным требованиям. Исследуйте получившиеся отклики системы. Во-первых, сравните получившуюся чувствительность S и дополнительная чувствительность T к соответствующим функциям взвешивания W1 и W3.

L = G*K;
I = eye(size(L));
S = feedback(I,L); 
T= I-S;

sigma(S,'b',W1,'b--',T,'r',W3,'r--',{0.1,1000})
legend('S','W1','T','W3')

График показывает тот S и T достигните желаемой формы цикла, где S является большим в пропускной способности управления, и мал вне пропускной способности управления.

Чтобы видеть, как формирование цикла смешанной чувствительности достигает целей классического формирования цикла, сравните ответ разомкнутого контура L к функциям взвешивания. L ~ W1 где W1 является большим, и L ~ 1/W3 где W3 является большим.

sigma(L,'b',W1,'r--',1/W3,'g--',{0.1,1000})
legend('L','W1','1/W3')

Смотрите также

augw | mixsyn

Документация