Подбирайте неопределенную модель к набору ответов LTI
usys = ucover(Parray,Pnom,ord)usys с номинальной стоимостью Pnom и чья область значений поведений включает все ответы в массив LTI Parray. Неопределенная структура модели имеет форму , где
Δ ultidyn объект, который представляет неопределенную динамику модульным усилением пика.
W является устойчивым, формирующий фильтром минимальной фазы порядка ord это настраивает сумму неопределенности на каждой частоте. Для MIMO Pnom, W является диагональным с порядками диагональных элементов, данных ord.
usys = ucover(Parray,Pnom,ord1,ord2,utype)utype.
utype = 'InputMult' — Введите мультипликативную форму, в который usys = Pnom*(I + W1*Delta*W2)
utype = 'OutputMult' — Выведите мультипликативную форму, в который usys = (I + W1*Delta*W2)*Pnom
utype = 'Additive' — Аддитивная форма, в который usys = Pnom + W1*Delta*W2
Delta представляет неопределенную динамику модульным усилением пика и W1 и W2 являются диагональными, устойчивыми, формирующий фильтры минимальной фазы с порядками, заданными ord1 и ord2, соответственно.
[ улучшает подгонку с помощью начальных значений фильтра в usys,info] = ucover(Pnom,info_in,ord1,ord2)info результат. Предоставьте новые порядки ord1 и ord2 для W1 и W2. Когда вы пробуете различных порядка фильтра, чтобы улучшить результат, этот синтаксис ускоряет итерацию путем разрешения вам, повторное использование ранее вычислило информацию.
Подбирайте неопределенную модель к массиву ответов LTI. Ответы могут быть, например, результатами нескольких запусков приобретения данных о частотной характеристике из физической системы.
В целях этого примера сгенерируйте данные о частотной характеристике путем создания массива моделей LTI и выборки частотной характеристики тех моделей.
Pnom = tf(2,[1 -2]); p1 = Pnom*tf(1,[.06 1]); p2 = Pnom*tf([-.02 1],[.02 1]); p3 = Pnom*tf(50^2,[1 2*.1*50 50^2]); array = stack(1,p1,p2,p3); Parray = frd(array,logspace(-1,3,60));
Данные о частотной характеристике в Parray представляет три отдельных эксперимента сбора данных в системе.
Постройте относительные погрешности между номинальным ответом объекта и этими тремя моделями в массиве LTI.
relerr = (Pnom-Parray)/Pnom; bodemag(relerr)
Если вы используете мультипликативную структуру модели неопределенности, величина формирующий фильтра должна соответствовать максимальным относительным погрешностям в каждой частоте.
Попробуйте формирующий фильтр 1-го порядка, чтобы соответствовать максимальным относительным погрешностям.
[P,Info] = ucover(Parray,Pnom,1);
P неопределенное пространство состояний (uss) модель, которая получает неопределенность как ultidyn неопределенный блок динамики.
P.Uncertainty
ans = struct with fields:
Parray_InputMultDelta: [1x1 ultidyn]
Info структура содержит другую информацию о подгонке, включая формирующий фильтр. Постройте ответ, чтобы видеть, как хорошо формирующий фильтр соответствует относительным погрешностям.
bodemag(relerr,'b--',Info.W1,'r',{0.1,1000});
График показывает что фильтр W1 слишком консервативно и превышает максимальную относительную погрешность в большинстве частот. Чтобы получить более плотно прилегающее, повторно выполните функцию с помощью фильтра 4-го порядка.
[P,Info] = ucover(Parray,Pnom,4);
Оцените подгонку путем графического вывода Предвещать графика величины.
bodemag(relerr,'b--',Info.W1,'r',{0.1,1000});
Этот график показывает это для фильтра 4-го порядка, величины W1 тесно совпадает с минимальной суммой неопределенности.
ucover приспосабливает ответы моделей LTI в Parray путем моделирования разрывов между Parray и номинальный ответ Pnom как неопределенность на системной динамике. Смоделировать плотность распределения этих несмоделированных движущих сил, ucover измеряет разрыв между Pnom и Parray на каждой частоте на сетке, и выбирает формирующий фильтры, величина которых аппроксимирует максимальный разрыв.
Спроектировать формирующий фильтры минимальной фазы W1 и W2, ucover команда выполняет два шага:
Вычисляет оптимальные значения W1 и W2 на сетке частоты.
Подгонки W1 и W2 значения с динамическими фильтрами заданного использования порядков fitmagfrd.
Структура модели то, что вы получаете использование usys = ucover(Parray,Pnom,ord), соответствует W1 = W и W2 = 1.
Например, следующий рисунок показывает относительный промежуток между номинальным ответом и шестью ответами LTI, окутанным использованием формирующий фильтра второго порядка и фильтра четвертого порядка.
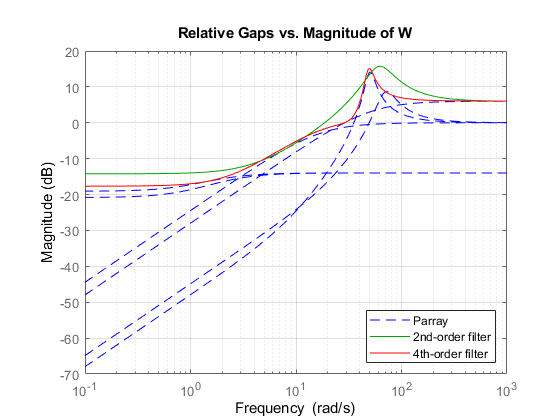
Если вы используете синтаксис одно фильтра usys = ucover(Parray,Pnom,ord), программное обеспечение устанавливает неопределенность на W*Delta, где Delta ultidyn объект, который представляет модульное усиление неопределенная динамика. Это гарантирует, что сумма неопределенности на каждой частоте задана величиной W и поэтому тесно отслеживает разрыв между Pnom и Parray. На вышеупомянутом рисунке фильтр четвертого порядка отслеживает максимальный разрыв более тесно и поэтому дает к менее осторожной оценке неопределенности.