Создание КИХ-фильтра линейной фазы наименьших квадратов
firls проектирует КИХ-фильтр линейной фазы, который минимизирует взвешенную интегрированную квадратичную невязку между идеальной кусочной линейной функцией и ответом величины фильтра по набору желаемых диапазонов частот.
Ссылка [2] описывает теоретический подход позади firls. Функция решает систему линейных уравнений, включающих матрицу скалярного произведения примерно размера n\2 использование MATLAB®
\ оператор.
Это тип I (n является нечетным) и тип II (n является четным), фильтры линейной фазы. Векторы f и a задайте амплитудные частотой характеристики фильтра:
f вектор из пар точек частоты, заданных в области значений от 0 до 1, где 1 соответствует частоте Найквиста. Частоты должны быть в увеличивающемся порядке. Дублирующиеся точки частоты позволены и, на самом деле, могут использоваться, чтобы спроектировать фильтр, который является точно тем же самым как фильтрами, возвращенными fir1 и fir2 функции с прямоугольным (rectwin) окно.
a вектор, содержащий желаемые амплитуды в точках, заданных в f.
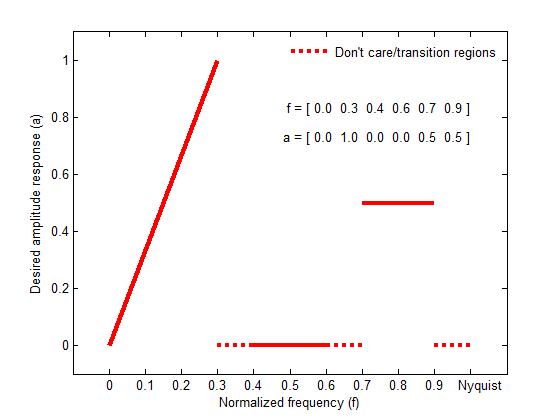
Желаемая амплитудная функция на частотах между парами точек (f (k), f (k +1)) для нечетного k является линейным сегментом, соединяющим точки (f (k), a (k)) и (f (k +1), a (k +1)).
Желаемая амплитудная функция на частотах между парами точек (f (k), f (k +1)) для k даже не задана. Это переход (“не заботятся”), области.
f и a та же длина. Эта длина должна быть четным числом.
Этот рисунок иллюстрирует отношение между f и a векторы в определении желаемого амплитудного ответа.
Эта функция проектирует тип I, II, III и фильтры линейной фазы IV. Тип I и II является фильтрами по умолчанию, когда n четен и нечетен, соответственно, в то время как 'hilbert' и 'differentiator' флаги производят тип III (n, является четным), и IV (n является нечетным), фильтры. Различные типы фильтра имеют различные симметрии и ограничения на их частотные характеристики (см. [1] для деталей).
| Линейный тип фильтра фазы | Порядок фильтра | Симметрия коэффициентов | Ответ H (f), f = 0 | Ответ H (f), f = 1 (Найквист) |
|---|---|---|---|---|
Тип I | Даже | Никакое ограничение | Никакое ограничение | |
Тип II | Нечетный | Никакое ограничение | H (1) = 0 | |
Тип III | Даже | H (0) = 0 | H (1) = 0 | |
Введите IV | Нечетный | H (0) = 0 | Никакое ограничение |
[1] Оппенхейм, Алан V, Рональд В. Шафер и Джон Р. Бак. Обработка сигналов дискретного времени. Верхний Сэддл-Ривер, NJ: Prentice Hall, 1999.
[2] Парки, Томас В. и К. Сидни Беррус. Создание цифровых фильтров. Хобокен, NJ: John Wiley & Sons, 1987, стр 54–83.
fir1 | fir2 | firpm | rcosdesign