Кратковременное преобразование Фурье
s = stft(___,Name,Value)
stft(___) без выходных аргументов строит величину STFT в окне текущей фигуры.
Сгенерируйте две секунды управляемого напряжением генератора выход, которым управляет синусоида, произведенная на уровне 10 кГц.
fs = 10e3; t = 0:1/fs:2; x = vco(sin(2*pi*t),[0.1 0.4]*fs,fs);
Вычислите и постройте STFT сигнала. Используйте окно Кайзера длины 256 и сформируйте параметр . Задайте длину перекрытия как 220 выборок и длина ДПФ как 512 точек. Постройте STFT с палитрой по умолчанию и представлением.
stft(x,fs,'Window',kaiser(256,5),'OverlapLength',220,'FFTLength',512);

Измените представление, чтобы отобразить STFT как график водопада. Установите палитру на jet.
view(-45,65)
colormap jet
Сгенерируйте квадратичный щебет, произведенный на уровне 1 кГц в течение 2 секунд. Мгновенная частота составляет 100 Гц в и кресты 200 Гц в второй.
ts = 0:1/1e3:2; f0 = 100; f1 = 200; x = chirp(ts,f0,1,f1,'quadratic',[],'concave');
Вычислите и отобразите STFT квадратичного щебета с длительностью 1 мс.
d = seconds(1e-3); win = hamming(100,'periodic'); stft(x,d,'Window',win,'OverlapLength',98,'FFTLength',128);

Сгенерируйте сигнал, произведенный на уровне 5 кГц в течение 4 секунд. Сигнал состоит из набора импульсов уменьшающейся длительности, разделенной областями колеблющейся амплитуды и колеблющейся частоты с увеличивающимся трендом. Постройте сигнал.
fs = 5000; t = 0:1/fs:4-1/fs; x = besselj(0,600*(sin(2*pi*(t+1).^3/30).^5)); plot(t,x)

Вычислите одностороннее, двухстороннее, и сосредоточил кратковременные преобразования Фурье сигнала. Во всех случаях используйте окно Кайзера с 202 выборками с масштабным фактором к окну сегменты сигнала. Отобразитесь частотный диапазон использовался для расчета каждого преобразования.
rngs = ["onesided" "twosided" "centered"]; for kj = 1:length(rngs) opts = {'Window',kaiser(202,10),'FrequencyRange',rngs(kj)}; [~,f] = stft(x,fs,opts{:}); subplot(length(rngs),1,kj) stft(x,fs,opts{:}) title(sprintf('''%s'': [%5.3f, %5.3f] kHz',rngs(kj),[f(1) f(end)]/1000)) end

Повторите расчет, но теперь измените длину окна Кайзера к 203, нечетное число. 'twosided' интервал частоты не изменяется. Другие два интервала частоты становятся открытыми на более верхнем уровне.
for kj = 1:length(rngs) opts = {'Window',kaiser(203,10),'FrequencyRange',rngs(kj)}; [~,f] = stft(x,fs,opts{:}); subplot(length(rngs),1,kj) stft(x,fs,opts{:}) title(sprintf('''%s'': [%5.3f, %5.3f] kHz',rngs(kj),[f(1) f(end)]/1000)) end

Сгенерируйте сигнал с тремя каналами, состоящий из трех различных щебетов, произведенных на уровне 1 кГц в течение одной секунды.
Первый канал состоит из вогнутого квадратичного щебета с мгновенной частотой 100 Гц в t = 0 и пересекает 300 Гц в t = 1 секунда. Это имеет начальную фазу, равную 45 градусам.
Второй канал состоит из выпуклого квадратичного щебета с мгновенной частотой 200 Гц в t = 0 и пересекает 600 Гц в t = 1 секунда.
Третий канал состоит из логарифмического щебета с мгновенной частотой 300 Гц в t = 0 и пересекает 500 Гц в t = 1 секунда.
Вычислите STFT многоканального сигнала с помощью периодического Окна Хэмминга длины 128 и продолжительности перекрытия 50 выборок.
fs = 1e3; t = 0:1/fs:1-1/fs; x = [chirp(t,100,1,300,'quadratic',45,'concave'); chirp(t,200,1,600,'quadratic',[],'convex'); chirp(t,300,1,500,'logarithmic')]'; [S,F,T] = stft(x,fs,'Window',hamming(128,'periodic'),'OverlapLength',50);
Визуализируйте STFT каждого канала как график водопада. Управляйте поведением осей с помощью функции помощника helperGraphicsOpt.
waterfall(F,T,abs(S(:,:,1))') helperGraphicsOpt(1)

waterfall(F,T,abs(S(:,:,2))') helperGraphicsOpt(2)

waterfall(F,T,abs(S(:,:,3))') helperGraphicsOpt(3)

Эта функция помощника устанавливает внешний вид и поведение текущей системы координат.
function helperGraphicsOpt(ChannelId) ax = gca; ax.XDir = 'reverse'; ax.ZLim = [0 30]; ax.Title.String = ['Input Channel: ' num2str(ChannelId)]; ax.XLabel.String = 'Frequency (Hz)'; ax.YLabel.String = 'Time (seconds)'; ax.View = [30 45]; end
x — Входной сигналВходной сигнал в виде вектора, матрицы или MATLAB®
timetable.
Примечание
Если вы инвертируете s использование istft и хочу результат быть той же длиной как x, значение (length(x)-noverlap)/(length(window)-noverlap) должно быть целое число.
Если вход имеет несколько каналов, задайте x как матрица, где каждый столбец соответствует каналу.
Для входа расписания, x должен содержать однородно увеличивающиеся конечные времена строки. Если расписание имеет пропавших без вести или дублирующиеся моменты времени, можно зафиксировать его с помощью советов в Чистом Расписании с Пропавшими без вести, Копией, или Неоднородные Времена.
Для многоканального входа расписания задайте x как расписание с одной переменной, содержащей матрицу или расписание с несколькими переменными каждый содержащий вектор-столбец. Все переменные должны иметь ту же точность.
Каждый канал x должен иметь длину, больше, чем длина окна.
Пример: chirp(0:1/4e3:2,250,1,500,'quadratic') задает одноканальный щебет.
Пример: timetable(rand(5,2),'SampleRate',1) задает двухканальную случайную переменную, произведенную на уровне 1 Гц в течение 4 секунд.
Пример: timetable(rand(5,1),rand(5,1),'SampleRate',1) задает двухканальную случайную переменную, произведенную на уровне 1 Гц в течение 4 секунд.
Типы данных: double | single
Поддержка комплексного числа: Да
fs — Частота дискретизацииЧастота дискретизации в виде положительной скалярной величины. Этот аргумент применяется только когда x вектор или матрица.
Типы данных: double | single
Задайте дополнительные разделенные запятой пары Name,Value аргументы. Name имя аргумента и Value соответствующее значение. Name должен появиться в кавычках. Вы можете задать несколько аргументов в виде пар имен и значений в любом порядке, например: Name1, Value1, ..., NameN, ValueN.
stft('Window',win,'OverlapLength',50,'FFTLength',128) окна данные с помощью окна win, с 50 выборками перекрываются между смежными сегментами и БПФ с 128 точками.'Window' — Спектральное окноhann(128,'periodic') (значение по умолчанию) | векторСпектральное окно в виде разделенной запятой пары, состоящей из 'Window' и вектор. Если вы не задаете окно или задаете его как пустой, функция использует окно Hann длины 128. Длина 'Window' должен быть больше или быть равен 2.
Для списка доступных окон смотрите Windows.
Пример: hann(N+1) и (1-cos(2*pi*(0:N)'/N))/2 оба задают окно Hann длины N + 1.
Типы данных: double | single
'OverlapLength' — Количество перекрытых выборокКоличество перекрытых выборок в виде разделенной запятой пары, состоящей из 'OverlapLength' и положительное целое число, меньшее, чем длина 'Window'. Если вы не используете 'OverlapLength' или задайте его как пустой, это установлено в самое большое целое число меньше чем 75% длины окна, которая является 96 выборками для окна Hann по умолчанию.
Типы данных: double | single
'FFTLength' — Количество точек ДПФКоличество ДПФ указывает в виде разделенной запятой пары, состоящей из 'FFTLength' и положительное целое число. Значение должно быть больше или быть равно длине окна. Если длина входного сигнала меньше длины ДПФ, данные дополнены нулями.
Типы данных: double | single
'FrequencyRange' — Частотный диапазон STFT'centered' (значение по умолчанию) | 'twosided' | 'onesided'Частотный диапазон STFT в виде разделенной запятой пары, состоящей из 'FrequencyRange' и 'centered', 'twosided', или 'onesided'.
'centered' — Вычислите двухсторонний, сосредоточенный STFT. Если nfft является четным, затем s вычисляется на интервале (–π, π] рад/выборка. Если nfft является нечетным, затем s вычисляется на интервале (–π, π) рад/выборка. Если вы указываете информацию времени, то интервалы (–fs, f s/2] циклы/единица времени и (–fs, f s/2) циклы/единица времени, соответственно, где f s является частотой дискретизации.
'twosided' — Вычислите двухсторонний STFT на интервале [0, 2π), рад/выборка. Если вы указываете информацию времени, то интервал [0, f s), циклы/единица времени.
'onesided' — Вычислите односторонний STFT. Если nfft является четным, затем s вычисляется на интервале [0, π] рад/выборка. Если nfft является нечетным, затем s вычисляется на интервале [0, π), рад/выборка. Если вы указываете информацию времени, то интервалы являются [0, f s/2] циклами/единицей времени и [0, f s/2), циклы/единица времени, соответственно, где f s является частотой дискретизации. Эта опция допустима только для действительных сигналов.
Примечание
Когда этот аргумент установлен в 'onesided', stft выводит значения в положительной области значений Найквиста и не сохраняет общую степень.
Для примера см. Частотные диапазоны STFT.
Типы данных: char | string
'OutputTimeDimension' — Выведите измерение времени'acrosscolumns' (значение по умолчанию) | 'downrows'Выведите измерение времени в виде разделенной запятой пары, состоящей из 'OutputTimeDimension' и 'acrosscolumns' или 'downrows'. Установите это значение к 'downrows' если вы хотите измерение времени s вниз строки и размерность частоты через столбцы. Установите это значение к 'acrosscolumns' если вы хотите измерение времени s через столбцы и размерность частоты вниз строки. Этот вход проигнорирован, если функция вызвана без выходных аргументов.
s — Кратковременное преобразование ФурьеКратковременное преобразование Фурье, возвращенное как матрица или трехмерный массив. Время увеличивается через столбцы s и частота увеличивает вниз строки. Третья размерность, если есть соответствует входным каналам.
Если x сигнала имеет выборки времени Nx, затем s имеет столбцы k, где k = ⌊ (Nx –L) / (M –L) ⌋, M является длиной 'Window', L является 'OverlapLength', и ⌊ ⌋ символы обозначают функцию пола.
Количество строк в s равно значению, заданному в 'FFTLength'.
Типы данных: double | single
f — ЧастотыЧастоты, на которых оценен STFT, возвратились как вектор.
Типы данных: double | single
t — Моменты времениМоменты времени, возвращенные как вектор. t содержит временные стоимости, соответствующие центрам использованных для расчета кратковременных оценок спектра мощности сегментов данных.
Если частота дискретизации fs обеспечивается, затем вектор содержит временные стоимости в секундах.
Если шаг расчета ts обеспечивается, затем вектор является массивом длительности с тем же форматом времени как вход.
Если никакая информация времени не предоставляется, то вектор содержит демонстрационные числа.
Типы данных: double | single
Кратковременное преобразование Фурье (STFT) используется, чтобы анализировать, как содержимое частоты неустановившегося сигнала изменяется в зависимости от времени.
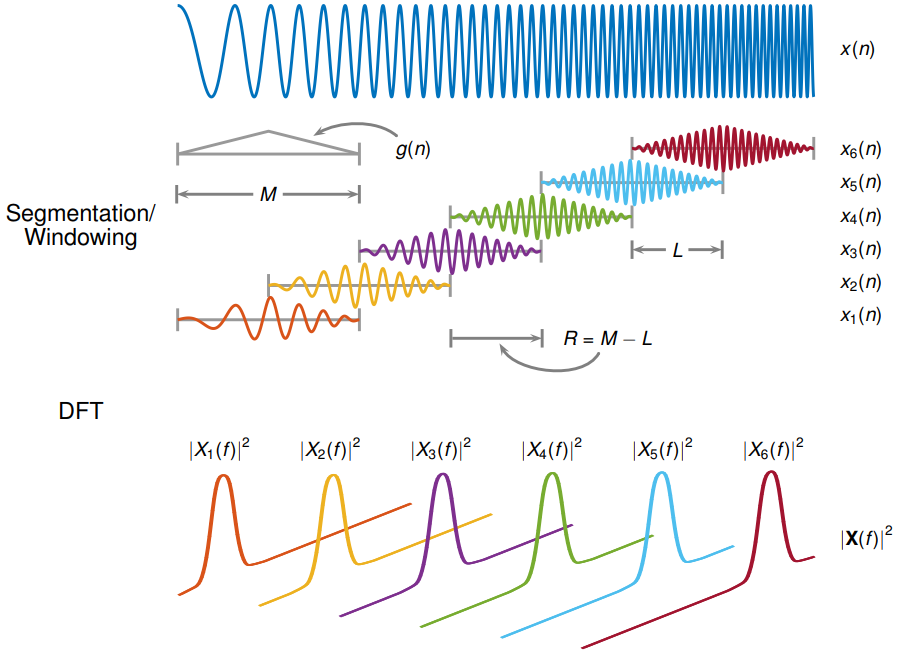
STFT сигнала вычисляется путем скольжения analysis window длины по сигналу и вычислению дискретного преобразования Фурье оконных данных. Окно скачкообразно двигается по исходному сигналу с промежутками в выборки. Функции окна Most сужаются в ребрах, чтобы избежать спектрального вызова. Если ненулевая длина перекрытия задан, добавление перекрытия, которое оконные сегменты компенсируют затухание сигнала в ребрах окна. ДПФ каждого оконного сегмента добавляется к матрице, которая содержит величину и фазу для каждого момента времени и частоты. Количество строк в матрице STFT равняется количеству точек ДПФ, и количеством столбцов дают
где длина исходного сигнала и ⌊⌋ символы обозначают функцию пола.
Матрицей STFT дают таким образом, что элемент th этой матрицы
где
— Функция окна длины .
— ДПФ оконных данных сосредоточен во время .
— Скачкообразно переместите размер между последовательными ДПФ, размер транзитного участка является различием между длиной окна и длина перекрытия .
Величина, в квадрате из STFT, уступает spectrogram представление степени спектральная плотность функции.
В общем случае вычисление STFT входного сигнала и инвертирование его не приводят к совершенной реконструкции. Если вы хотите, чтобы выход ISTFT совпадал с исходным входным сигналом максимально тесно, сигнал и окно должны удовлетворить следующим условиям:
Введите размер — Если вы инвертируете выход stft использование istft и хочу результат быть той же длиной как входной сигнал x, значение должно быть целое число.
Податливость COLA — Использование совместимые КОЛОЙ окна, принимая, что вы не изменили кратковременное преобразование Фурье сигнала.
Дополнение — Если длина входного сигнала такова, что значение k не является целым числом, нулевая клавиатура сигнал прежде, чем вычислить кратковременное преобразование Фурье. Удалите дополнительные нули после инвертирования сигнала.
[1] Mitra, цифровая обработка сигналов Сэнджита К.: компьютерный подход. 2-й Эд. Нью-Йорк: McGraw-Hill, 2001.
[2] Шарп, Брюс. Обратимость Перекрытия - Добавляет Обработку. https://gauss256.github.io/blog/cola.html, получил доступ к июлю 2019.
[3] Смит, Джулиус Орайон. Спектральная Обработка Звукового сигнала. https://ccrma.stanford.edu / ~ jos/sasp/, онлайновая книга, 2 011 выпусков, получил доступ к ноябрю 2018.
Указания и ограничения по применению:
'OutputTimeDimension' должен всегда задаваться и устанавливаться в 'downrows'.
Для получения дополнительной информации см. Раздел "Высокие массивы".
Указания и ограничения по применению:
Расписания не поддерживаются для генерации кода.
Указания и ограничения по применению:
Расписания не поддерживаются для генерации кода.
Эта функция полностью поддерживает массивы графического процессора. Для получения дополнительной информации смотрите функции MATLAB Запуска на графическом процессоре (Parallel Computing Toolbox).
У вас есть модифицированная версия этого примера. Вы хотите открыть этот пример со своими редактированиями?
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.