Exponenta Banner

resubLoss

Потеря k - самый близкий соседний классификатор перезаменой

свернуть все на странице

Синтаксис

L = resubLoss(mdl)
L = resubLoss(mdl,'LossFun',lossfun)

Описание

пример

L = resubLoss(mdl) возвращает ущерб классификации от перезамены, которая является потерей, вычисленной для данных, используемых fitcknn создать mdl.

Потеря классификации (L) числовой скаляр, интерпретация которого зависит от функции потерь и весов наблюдения в mdl.

L = resubLoss(mdl,'LossFun',lossfun) возвращает потерю перезамены для функции потерь lossfunВ виде аргумента пары "имя-значение".

Примеры

свернуть все

Скрипт Open Live Script

Создайте классификатор k - ближайших соседей для ирисовых данных Фишера, где k = 5.

Загрузите ирисовый набор данных Фишера. 

load fisheriris

Создайте классификатор для пяти самых близких соседей. 

mdl = fitcknn(meas,species,'NumNeighbors',5);

Исследуйте потерю перезамены классификатора. 

L = resubLoss(mdl)
L = 0.0333

Классификатор предсказывает неправильные классификации для 1/30 его обучающих данных.

Входные параметры

свернуть все

модель классификатора k - ближайших соседей в виде ClassificationKNN объект.

Функция потерь в виде встроенного имени функции потерь или указателя на функцию.

  • В следующей таблице перечислены доступные функции потерь.

    ЗначениеОписание
    'binodeviance'Биномиальное отклонение
    'classiferror'Ошибка классификации
    'exponential'Экспоненциал
    'hinge'Стержень
    'logit'Логистический
    'mincost'Минимальный ожидал стоимость misclassification (для классификационных оценок, которые являются апостериорными вероятностями),
    'quadratic'Квадратичный

    'mincost' подходит для классификационных оценок, которые являются апостериорными вероятностями. По умолчанию k - самые близкие соседние модели возвращают апостериорные вероятности как классификационные оценки (см. predict).

  • Можно задать указатель на функцию для пользовательской функции потерь с помощью @ (например, @lossfun). Позвольте n быть количеством наблюдений в X и K быть количеством отличных классов (numel(mdl.ClassNames)). Ваша пользовательская функция потерь должна иметь эту форму:

    function lossvalue = lossfun(C,S,W,Cost)

    • C n-by-K логическая матрица со строками, указывающими на класс, которому принадлежит соответствующее наблюдение. Порядок следования столбцов соответствует порядку класса в mdl.ClassNames. Создайте C установкой C(p,q) = 1, если наблюдение p находится в классе q, для каждой строки. Установите все другие элементы строки p к 0.

    • S n-by-K числовая матрица классификационных оценок. Порядок следования столбцов соответствует порядку класса в mdl.ClassNames. Аргумент S матрица классификационных оценок, похожих на выход predict.

    • W n-by-1 числовой вектор из весов наблюдения. Если вы передаете W, программное обеспечение нормирует веса, чтобы суммировать к 1.

    • Cost K-by-K числовая матрица затрат misclassification. Например, Cost = ones(K) – eye(K) задает стоимость 0 для правильной классификации и 1 для misclassification.

    • Выходной аргумент lossvalue скаляр.

Для получения дополнительной информации о функциях потерь смотрите Потерю Классификации.

Типы данных: char | string | function_handle

Алгоритмы

свернуть все

Потеря классификации

Функции Classification loss измеряют прогнозирующую погрешность моделей классификации. Когда вы сравниваете тот же тип потери среди многих моделей, более низкая потеря указывает на лучшую прогнозную модель.

Рассмотрите следующий сценарий.

  • L является средневзвешенной потерей классификации.

  • n является объемом выборки.

  • Для бинарной классификации:

    • yj является наблюдаемой меткой класса. Программные коды это как –1 или 1, указывая на отрицательный или положительный класс, соответственно.

    • f (Xj) является необработанной классификационной оценкой для наблюдения (строка) j данных о предикторе X.

    • mj = yj f (Xj) является классификационной оценкой для классификации наблюдения j в класс, соответствующий yj. Положительные значения mj указывают на правильную классификацию и не способствуют очень средней потере. Отрицательные величины mj указывают на неправильную классификацию и значительно способствуют средней потере.

  • Для алгоритмов, которые поддерживают классификацию мультиклассов (то есть, K ≥ 3):

    • yj* является вектором из K – 1 нуль, с 1 в положении, соответствующем истинному, наблюдаемому классу yj. Например, если истинный класс второго наблюдения является третьим классом и K = 4, то y 2* = [0 0 1 0] ′. Порядок классов соответствует порядку в ClassNames свойство входной модели.

    • f (Xj) является длиной вектор K из музыки класса к наблюдению j данных о предикторе X. Порядок баллов соответствует порядку классов в ClassNames свойство входной модели.

    • mj = yj* ′ f (Xj). Поэтому mj является скалярной классификационной оценкой, которую модель предсказывает для истинного, наблюдаемого класса.

  • Весом для наблюдения j является wj. Программное обеспечение нормирует веса наблюдения так, чтобы они суммировали к соответствующей предшествующей вероятности класса. Программное обеспечение также нормирует априорные вероятности, таким образом, они суммируют к 1. Поэтому

    ∑j=1nwj=1.

Учитывая этот сценарий, следующая таблица описывает поддерживаемые функции потерь, которые можно задать при помощи 'LossFun' аргумент пары "имя-значение".

Функция потерьЗначение LossFunУравнение
Биномиальное отклонение'binodeviance'L=∑j=1nwjlog{1+exp[−2mj]}.
Экспоненциальная потеря'exponential'L=∑j=1nwjexp(−mj).
Ошибка классификации'classiferror'

L=∑j=1nwjI{y^j≠yj}.

Ошибка классификации является взвешенной частью неправильно классифицированных наблюдений где y^j метка класса, соответствующая классу с максимальной апостериорной вероятностью. I {x} является функцией индикатора.

Потеря стержня'hinge'L=∑j=1nwjmax{0,1−mj}.
Потеря логита'logit'L=∑j=1nwjlog(1+exp(−mj)).
Минимальная стоимость'mincost'

Программное обеспечение вычисляет взвешенную минимальную стоимость с помощью этой процедуры для наблюдений j = 1..., n.

  1. Оцените 1 K вектором из ожидаемых затрат классификации для наблюдения j:

    γj=f(Xj)′C.

    f (Xj) является вектор-столбцом апостериорных вероятностей класса для классификации мультиклассов и двоичного файла. C является матрицей стоимости, сохраненной входной моделью в Cost свойство.

  2. Для наблюдения j предскажите метку класса, соответствующую минимальной ожидаемой стоимости классификации:

    y^j=minj=1,...,K(γj).

  3. Используя C, идентифицируйте, что стоимость подверглась (cj) для того, чтобы сделать предсказание.

Взвешенная, средняя, минимальная потеря стоимости

L=∑j=1nwjcj.

Квадратичная потеря'quadratic'L=∑j=1nwj(1−mj)2.

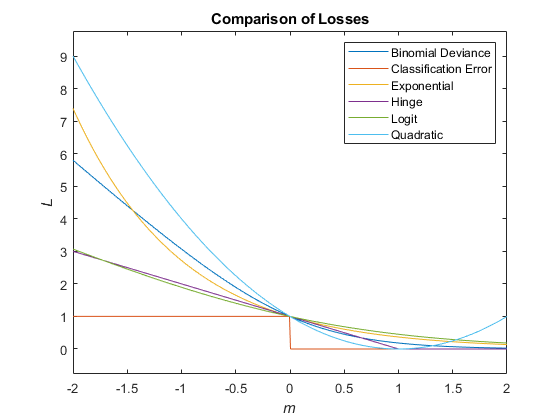
Этот рисунок сравнивает функции потерь (кроме 'mincost') для одного наблюдения по m. Некоторые функции нормированы, чтобы пройти [0,1].

Comparison of classification losses for different loss functions

Истинная стоимость Misclassification

Два затрат сопоставлены с классификацией KNN: истинная стоимость misclassification в классе и ожидаемом misclassification стоится на наблюдение.

Можно установить истинную стоимость misclassification в классе при помощи 'Cost' аргумент пары "имя-значение", когда вы запускаетесь fitcknn. Значение Cost(i,j) стоимость классификации наблюдения в класс j если его истинным классом является i. По умолчанию, Cost(i,j) = 1 если i ~= j, и Cost(i,j) = 0 если i = j. Другими словами, стоимостью является 0 для правильной классификации и 1 для неправильной классификации.

Ожидаемая стоимость

Два затрат сопоставлены с классификацией KNN: истинная стоимость misclassification в классе и ожидаемом misclassification стоится на наблюдение. Третий выход resubPredict ожидаемая стоимость misclassification на наблюдение.

Предположим, что у вас есть Nobs наблюдения, что вы классифицировали с обученным классификатором mdl, и у вас есть K классы. Команда

[label,score,cost] = resubPredict(mdl)

возвращает матричный cost из размера Nobs- K, среди других выходных параметров. Каждая строка cost матрица содержит ожидаемую (среднюю) стоимость классификации наблюдения в каждый K классы. cost(n,j)

∑i=1KP^(i|X(n))C(j|i),

где

  • K является количеством классов.

  • P^(i|X(n)) апостериорная вероятность класса i для наблюдения X (n).

  • C(j|i) истинная misclassification стоимость классификации наблюдения как j, когда его истинным классом является i.

Смотрите также

| | | |

Темы

Представленный в R2012a

Документация Statistics and Machine Learning Toolbox

Поддержка