Чтобы проиллюстрировать, как взять производные с помощью программного обеспечения Symbolic Math Toolbox™, сначала создайте символьное выражение:
syms x f = sin(5*x);
Команда
diff(f)
дифференцирует f относительно x:
ans = 5*cos(5*x)
Как другой пример, позволить
g = exp(x)*cos(x);
где exp(x) обозначает ex, и дифференцируют g:
y = diff(g)
y = exp(x)*cos(x) - exp(x)*sin(x)
Найти производную g для данного значения x, замените x для использования значения subs и возвратите использование численного значения vpa. Найдите производную g в x = 2.
vpa(subs(y,x,2))
ans = -9.7937820180676088383807818261614
Взять вторую производную g, войти
diff(g,2)
ans = -2*exp(x)*sin(x)
Можно получить тот же результат путем взятия производной дважды:
diff(diff(g))
ans = -2*exp(x)*sin(x)
В этом примере MATLAB автоматически упрощает ответ. Однако в некоторых случаях MATLAB не может упростить ответ, в этом случае можно использовать simplify команда. Для примера такого упрощения смотрите Больше Примеров.
Обратите внимание на то, что, чтобы взять производную константы, необходимо сначала задать константу как символьное выражение. Например, ввод
c = sym('5');
diff(c)возвращается
ans = 0
Если вы только входите
diff(5)
MATLAB возвращается
ans =
[]потому что 5 не символьное выражение.
Чтобы дифференцировать выражение, которое содержит больше чем одну символьную переменную, задайте переменную, относительно которой вы хотите дифференцироваться. diff команда затем вычисляет частную производную выражения относительно той переменной. Например, учитывая символьное выражение
syms s t f = sin(s*t);
команда
diff(f,t)
вычисляет частную производную . Результат
ans = s*cos(s*t)
Дифференцировать f относительно переменной s, войти
diff(f,s)
который возвращается:
ans = t*cos(s*t)
Если вы не задаете переменную, чтобы дифференцироваться относительно, MATLAB выбирает переменную по умолчанию. В основном переменная по умолчанию является буквой, самой близкой к x в алфавите. Смотрите полный набор правил в Находке Символьная Переменная По умолчанию. В предыдущем примере, diff(f) берет производную f относительно t потому что буква t ближе к x в алфавите, чем буква s . Чтобы определить переменную по умолчанию, относительно которой дифференцируется MATLAB, использовать symvar:
symvar(f, 1)
ans = t
Вычислите вторую производную f относительно t:
diff(f, t, 2)
Эта команда возвращается
ans = -s^2*sin(s*t)
Обратите внимание на то, что diff(f, 2) дает тот же ответ потому что t переменная по умолчанию.
Далее проиллюстрировать diff команда, задайте aBXNT, и theta в рабочем пространстве MATLAB путем ввода
syms a b x n t theta
Эта таблица иллюстрирует результаты ввода diff(f).
f | diff (f) |
|---|---|
syms x n f = x^n; | diff(f) ans = n*x^(n - 1) |
syms a b t f = sin(a*t + b); | diff(f) ans = a*cos(b + a*t) |
syms theta f = exp(i*theta); | diff(f) ans = exp(theta*1i)*1i |
Дифференцировать функцию Бесселя первого рода, besselj(nu,z), относительно zВвод
syms nu z b = besselj(nu,z); db = diff(b)
который возвращается
db = (nu*besselj(nu, z))/z - besselj(nu + 1, z)
diff функция может также взять символьную матрицу в качестве своего входа. В этом случае дифференцирование сделано поэлементно. Рассмотрите пример
syms a x A = [cos(a*x),sin(a*x);-sin(a*x),cos(a*x)]
который возвращается
A = [ cos(a*x), sin(a*x)] [ -sin(a*x), cos(a*x)]
Команда
diff(A)
возвращается
ans = [ -a*sin(a*x), a*cos(a*x)] [ -a*cos(a*x), -a*sin(a*x)]
Можно также выполнить дифференцирование вектор-функции относительно аргумента вектора. Рассмотрите преобразование от Евклидова (x, y, z) к сферическому координаты, как дано , , и . Обратите внимание на то, что соответствует вертикальному изменению или широте в то время как обозначает азимут или долготу.
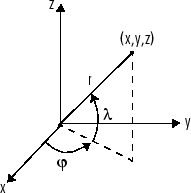
Чтобы вычислить якобиевскую матрицу, J, этого преобразования, использует jacobian функция. Математическое обозначение for J
В целях синтаксиса тулбокса используйте l для и f для . Команды
syms r l f x = r*cos(l)*cos(f); y = r*cos(l)*sin(f); z = r*sin(l); J = jacobian([x; y; z], [r l f])
возвратите якобиан
J = [ cos(f)*cos(l), -r*cos(f)*sin(l), -r*cos(l)*sin(f)] [ cos(l)*sin(f), -r*sin(f)*sin(l), r*cos(f)*cos(l)] [ sin(l), r*cos(l), 0]
и команда
detJ = simplify(det(J))
возвращается
detJ = -r^2*cos(l)
Аргументы jacobian функция может быть вектор-столбцами или векторами-строками. Кроме того, поскольку определитель якобиана является довольно сложным тригонометрическим выражением, можно использовать simplify сделать тригонометрические замены и сокращения (упрощения).
Таблица, обобщающая diff и jacobian следует.
Математический оператор | Команда MATLAB |
|---|---|
| |
| |
| |
|