Постройте символьное выражение или функцию
fplot( графики f,[xmin xmax])f на интервале [xmin xmax].
fplot( графики xt = x (t) и yt = y (t) по заданной области xt,yt,[tmin
tmax])[tmin tmax].
fplot(___, использование LineSpec)LineSpec установить стиль линии, символ маркера и цвет линии.
fplot(___, задает свойства линии с помощью одного или нескольких Name,Value)Name,Value парные аргументы. Используйте эту опцию с любыми комбинациями входных аргументов в предыдущих синтаксисах. Name,Value парные настройки применяются ко всем построенным графикам. Чтобы установить опции для отдельных линий, используйте объекты, возвращенные fplot.
fplot( графики в оси заданы ax,___)ax вместо текущей системы координат gca.
fp = fplot(___)
Постройте tan(x) в области значений по умолчанию [-5 5]fplot показывает полюса по умолчанию. Для получения дополнительной информации смотрите ShowPoles аргумент в Аргументах в виде пар имя-значение.
syms x
fplot(tan(x))
Постройте символьную функцию в области значений по умолчанию [-5 5].
syms f(x)
f(x) = cos(x);
fplot(f)
Постройте параметрическую кривую и .
syms t
x = cos(3*t);
y = sin(2*t);
fplot(x,y)
График путем определения интервала графического вывода как второго входа к fplot.
syms x
fplot(sin(x),[-pi/2 pi/2])
Можно построить несколько графиков или путем передачи входных параметров как вектора или при помощи hold on последовательно построить на той же фигуре. Если вы задаете LineSpec и аргументы Name-Value, они применяются ко всем линиям. Чтобы установить опции для отдельных участков, используйте указатели на функцию, возвращенные fplot.
Разделите фигуру на два подграфика с помощью subplot. На первом подграфике, графике и использование векторного входа. На втором подграфике, графике и использование hold on.
syms x subplot(2,1,1) fplot([sin(x) cos(x)]) title('Multiple Lines Using Vector Inputs') subplot(2,1,2) fplot(sin(x)) hold on fplot(cos(x)) title('Multiple Lines Using hold on Command') hold off

Постройте три синусоиды со сдвигом фазы между каждой линией. Для первой линии используйте linewidth 2. Для второго задайте пунктирный стиль красной линии с круговыми маркерами. Для третьего задайте голубой стиль штрихпунктирной линии с маркерами звездочки. Отобразите легенду.
syms x fplot(sin(x+pi/5),'Linewidth',2) hold on fplot(sin(x-pi/5),'--or') fplot(sin(x),'-.*c') legend('show','Location','best') hold off

Управляйте разрешением графика при помощи MeshDensity опция. Увеличение MeshDensity может сделать более сглаженные, более точные графики, в то время как уменьшение его может увеличить скорость графического вывода.
Разделите фигуру на два при помощи subplot. В первом подграфике постройте ступенчатую функцию от x = 2.1 к x = 2.15. Разрешение графика является слишком низким, чтобы обнаружить ступенчатую функцию. Устраните эту проблему путем увеличения MeshDensity к 39 во втором подграфике. График теперь обнаруживает ступенчатую функцию и показывает это путем увеличения MeshDensity вы увеличили разрешение графика.
syms x stepFn = rectangularPulse(2.1, 2.15, x); subplot(2,1,1) fplot(stepFn); title('Default MeshDensity = 23') subplot(2,1,2) fplot(stepFn,'MeshDensity',39); title('Increased MeshDensity = 39')

Постройте sin(x). Задайте выход, чтобы сделать fplot возвратите объект графика.
syms x
h = fplot(sin(x))
h =
FunctionLine with properties:
Function: [1x1 sym]
Color: [0 0.4470 0.7410]
LineStyle: '-'
LineWidth: 0.5000
Show all properties
Измените синюю линию по умолчанию в пунктирную красную линию при помощи записи через точку, чтобы установить свойства. Точно так же добавьте 'x' маркеры и набор цвет маркера к синему.
h.LineStyle = '--'; h.Color = 'r'; h.Marker = 'x'; h.MarkerEdgeColor = 'b';

Для от к график . Добавьте заголовок и подписи по осям. Создайте метки деления оси X путем охвата пределов оси X с промежутками в pi/2. Отобразите эти метки деления при помощи XTick свойство. Создайте метки оси X при помощи arrayfun применять texlabel к S. Отобразите эти метки при помощи XTickLabel свойство.
Чтобы использовать LaTeX в графиках, смотрите latex.
syms x fplot(sin(x),[-2*pi 2*pi]) grid on title('sin(x) from -2\pi to 2\pi') xlabel('x') ylabel('y') ax = gca; S = sym(ax.XLim(1):pi/2:ax.XLim(2)); ax.XTick = double(S); ax.XTickLabel = arrayfun(@texlabel,S,'UniformOutput',false);

Когда вы масштабируете в график, fplot переоценивает график автоматически. Эта переоценка на изменении масштаба показывает скрытую деталь в меньших масштабах.
Постройте x^3*sin(1/x) для -2 < x < 2 и -0.02 < y < 0.02. Увеличьте масштаб использования графика zoom и перерисуйте использование графика drawnow. Из-за переоценки на изменении масштаба, fplot показывает деталь меньшего масштаба. Повторите изменение масштаба 6 раз, чтобы посмотреть детали меньшего масштаба. Чтобы проигрывать анимацию, нажмите на изображение.
syms x fplot(x^3*sin(1/x)); axis([-2 2 -0.02 0.02]); for i=1:6 zoom(1.7) pause(0.5) end
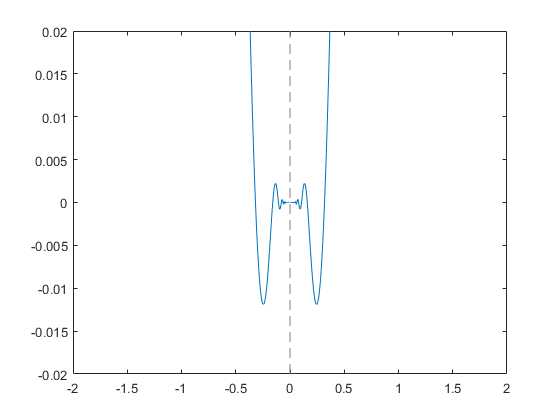
Создайте анимации путем изменения отображенного выражения с помощью FunctionXFunction , и YFunction свойства и затем при помощи drawnow обновить график. Чтобы экспортировать в GIF, смотрите imwrite.
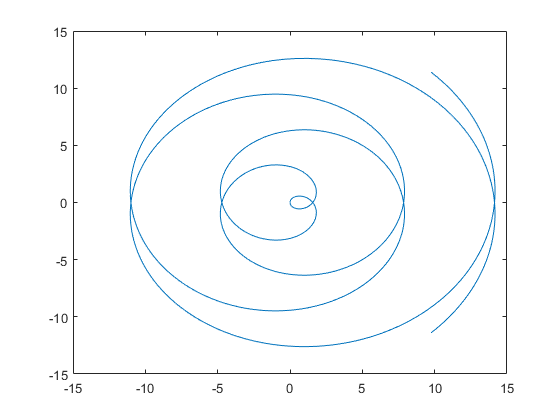
Путем варьирования переменной i от 0,1 до 3, анимируйте параметрическую кривую
Чтобы проигрывать анимацию, нажмите на изображение.
syms t fp = fplot(t, t); axis([-15 15 -15 15]) for i=0.1:0.05:3 fp.XFunction = i.*t.*sin(i*t); fp.YFunction = i.*t.*cos(i*t); drawnow end
Если fplot обнаруживает конечное число разрывов в fто fplot расширяет область значений, чтобы показать им.