idwt2
Одноуровневый обратный дискретный 2D вейвлет преобразовывает
Синтаксис
Описание
x = idwt2(cA,cH,cV,cD,wname)cA и матрицы деталей cH, cV, и cD (горизонталь, вертикальная, и диагональная, соответственно), использование вейвлета задано wname. Для получения дополнительной информации смотрите dwt2.
Позвольте sa = размер (, и позвольте cA) = размер (cH) = размер (cV) = размер (cD)lf равняйтесь длине фильтров реконструкции, сопоставленных с wname. Если дополнительный режим DWT установлен в periodization, размер x, sx равно 2*sa. Для других дополнительных режимов, sx = 2*sa-lf+2. Для получения дополнительной информации смотрите dwtmode.
x = idwt2(___,s)s центральный фрагмент реконструкции с помощью любого из предыдущих синтаксисов.
x = idwt2(cA,[],[],[],___)x на основе содействующей матрицы приближения cA.
x = idwt2([],cH,[],[],___)x на основе горизонтальной содействующей матрицы детали cH.
x = idwt2([],[],cV,[],___)x на основе вертикальной содействующей матрицы детали cV.
Примеры
Одноуровневая 2D реконструкция вейвлета
Загрузите изображение.
load woman whos X
Name Size Bytes Class Attributes X 256x256 524288 double
Переменная X рабочей области содержит изображение. Выполните одноуровневое разложение вейвлета X используйте db4 вейвлет.
[cA1,cH1,cV1,cD1] = dwt2(X,'db4');Инвертируйте разложение X использование коэффициентов на уровне 1.
A0 = idwt2(cA1,cH1,cV1,cD1,'db4');Проверяйте на совершенную реконструкцию.
max(abs(X(:)-A0(:)))
ans = 3.4174e-10
Реконструкция вейвлета коэффициентов детали
Загрузите изображение.
load tartan
imagesc(X)
colormap(gray)
Выполните одноуровневое разложение вейвлета с помощью db4 вейвлет.
[cA,cH,cV,cD] = dwt2(X,'db4');Получите реконструкцию вейвлета с помощью только диагональные коэффициенты детали.
xrecD = idwt2([],[],[],cD,'db4');Получите вторую реконструкцию вейвлета, на этот раз с помощью горизонтальных и диагональных коэффициентов детали.
xrecHD = idwt2([],cH,[],cD,'db4');Отобразите обе реконструкции.
subplot(1,2,1) imagesc(xrecD) title('Diagonal') subplot(1,2,2) imagesc(xrecHD) title('Horizontal-Diagonal') colormap(gray)
Входные параметры
Советы
Алгоритмы
2D алгоритм реконструкции вейвлета для изображений похож на одномерный случай. Двумерный вейвлет и масштабирующиеся функции получены путем взятия продуктов тензора одномерного вейвлета и масштабирования функций. Этот вид двумерного обратного DWT приводит к реконструкции коэффициентов приближения на уровне j от четырех компонентов: приближение на уровне j +1 и детали в трех ориентациях (горизонталь, вертикальная, и диагональная). Следующий график описывает основные шаги реконструкции для изображений.
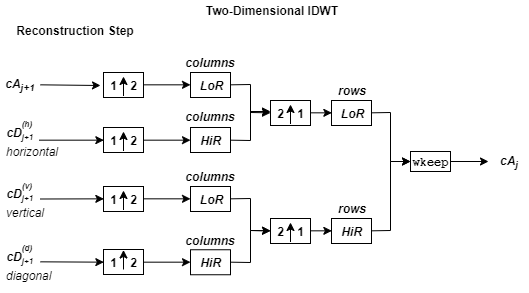
где
— Сверхдискретизируйте столбцы: вставьте нули в нечетных индексированных столбцах
— Сверхдискретизируйте строки: вставьте нули в нечетно индексированных строках
— Примените операцию свертки с фильтром X строки записи
— Примените операцию свертки с фильтром X столбцы записи
Ссылки
[1] Daubechies, Ингрид. Десять лекций по вейвлетам. CBMS-NSF региональный ряд конференции в прикладной математике 61. Филадельфия, Па: общество промышленной и прикладной математики, 1992.
[2] Mallat, S.G. “Теория для Разложения Сигнала Мультиразрешения: Представление Вейвлета”. Транзакции IEEE согласно Анализу Шаблона и Искусственному интеллекту 11, № 7 (июль 1989): 674–93. https://doi.org/10.1109/34.192463.
[3] Мейер, Y. Вейвлеты и операторы. Переведенный Д. Х. Сэлинджером. Кембридж, Великобритания: Издательство Кембриджского университета, 1995.