Дискретный стационарный вейвлет преобразовывает 1D
Учитывая s сигнала длины N, первый шаг стационарного вейвлета преобразовывает (SWT) производит, начинающий с s, двух наборов коэффициентов: коэффициенты приближения cA1 и коэффициенты детали cD1. Эти векторы получены путем свертки к s с фильтром lowpass LoD для приближения, и с highpass фильтруют HiD для детали.
Более точно первый шаг
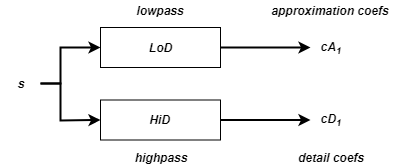
где![]() обозначает свертку с фильтром X.
обозначает свертку с фильтром X.
Примечание
cA1 и cD1 имеют длину N вместо N/2 как в случае DWT.
Следующий шаг разделяет коэффициенты приближения cA1 в двух частях с помощью той же схемы, но с модифицированными фильтрами, полученными путем повышающей дискретизации фильтров, используемых для предыдущего шага и заменяющий s cA1. Затем SWT производит cA2 и cD2. В более общем плане,
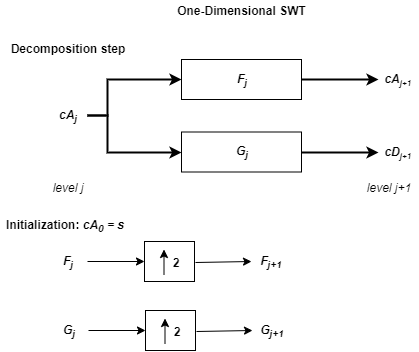
где
F 0 = LoD
G 0 = HiD
![]() — Сверхдискретизируйте (вставьте нули между элементами),
— Сверхдискретизируйте (вставьте нули между элементами),
[1] Нэзон, G. P. и Б. В. Сильверман. “Стационарное Преобразование Вейвлета и Некоторые Статистические Приложения”. В Вейвлетах и Статистике, отредактированной Анестисом Антониэдисом и Жоржем Оппенхеймом, 103:281–99. Нью-Йорк, Нью-Йорк: Спрингер Нью-Йорк, 1995. https://doi.org/10.1007/978-1-4612-2544-7_17.
[2] Койфман, R. R. и Д. Л. Донохо. “Инвариантное переводом Шумоподавление”. В Вейвлетах и Статистике, отредактированной Анестисом Антониэдисом и Жоржем Оппенхеймом, 103:125–50. Нью-Йорк, Нью-Йорк: Спрингер Нью-Йорк, 1995. https://doi.org/10.1007/978-1-4612-2544-7_9.
[3] Pesquet, J.-C., Х. Крим и Х. Карфэнтэн. “Независимые от времени Ортонормированные Представления Вейвлета”. Транзакции IEEE на Обработке сигналов 44, № 8 (август 1996): 1964–70. https://doi.org/10.1109/78.533717.