Скалярное квантование является процессом, который сопоставляет все входные параметры в заданной области к общему значению. Это карты процессов вводит в различной области значений значений к различному общему значению. В действительности скалярное квантование оцифровывает аналоговый сигнал. Два параметра определяют квантование: раздел и книга шифров.
Раздел квантования задает несколько непрерывных, неперекрывающихся областей значений значений в наборе вещественных чисел. Чтобы задать раздел в среде MATLAB®, перечислите отличные конечные точки различных областей значений в векторе.
Например, если раздел разделяет линию вещественного числа на четыре набора
X: x ≤ 0}
X: 0 <x ≤ 1}
X: 1 <x ≤ 3}
X: 3 <x}
затем можно представлять раздел как трехэлементный вектор
partition = [0,1,3];
Длина вектора раздела является той меньше, чем количество интервалов раздела.
Книга шифров говорит квантизатор, какое общее значение присвоить входным параметрам, которые попадают в каждую область значений раздела. Представляйте книгу шифров как вектор, длина которого совпадает с количеством интервалов раздела. Например, вектор
codebook = [-1, 0.5, 2, 3];
одна возможная книга шифров для раздела [0,1,3].
quantiz функционируйте также возвращает вектор, который говорит, в каком интервале каждый вход находится. Например, выход ниже говорит, что входные записи лежат в интервалах, помеченных 0, 6, и 5, соответственно. Здесь, 0th интервал состоит из вещественных чисел, меньше чем или равных 3; 6-й интервал состоит из вещественных чисел, больше, чем 8, но меньше чем или равный 9; и 5-й интервал состоит из вещественных чисел, больше, чем 7, но меньше чем или равный 8.
partition = [3,4,5,6,7,8,9]; index = quantiz([2 9 8],partition)
Выход
index =
0
6
5
Если вы продолжаете этот пример путем определения вектора книги шифров такой как
codebook = [3,3,4,5,6,7,8,9];
затем уравнение ниже связывает векторный index к квантованному quants сигнала.
quants = codebook(index+1);
Эта формула для quants точно что quantiz функционируйте использование, если вы вместо этого формулируете пример более кратко как ниже.
partition = [3,4,5,6,7,8,9]; codebook = [3,3,4,5,6,7,8,9]; [index,quants] = quantiz([2 9 8],partition,codebook);
Квантование искажает сигнал. Можно уменьшать искажение путем выбора соответствующего раздела и параметров книги шифров. Однако тестирование и выбор параметров для больших наборов сигнала с прекрасной схемой квантования могут быть утомительными. Один способ произвести раздел и параметры книги шифров легко состоит в том, чтобы оптимизировать их согласно набору так называемых обучающих данных.
Примечание
Обучающие данные, которые вы используете, должны быть типичны для видов сигналов, которые вы будете на самом деле квантовать.
lloyds функция оптимизирует раздел и книгу шифров согласно алгоритму Ллойда. Код ниже оптимизирует раздел и книгу шифров в течение одного периода синусоидального сигнала, начинающего с грубого исходного предположения. Затем это использует эти параметры, чтобы квантовать исходный сигнал с помощью параметров исходного предположения, а также оптимизированных параметров. Выход показывает, что среднеквадратическое искажение после квантования намного меньше для оптимизированных параметров. quantiz функция автоматически вычисляет среднеквадратическое искажение и возвращает его как третий выходной параметр.
% Start with the setup from 2nd example in "Quantizing a Signal." t = [0:.1:2*pi]; sig = sin(t); partition = [-1:.2:1]; codebook = [-1.2:.2:1]; % Now optimize, using codebook as an initial guess. [partition2,codebook2] = lloyds(sig,codebook); [index,quants,distor] = quantiz(sig,partition,codebook); [index2,quant2,distor2] = quantiz(sig,partition2,codebook2); % Compare mean square distortions from initial and optimized [distor, distor2] % parameters.
Выход
ans =
0.0148 0.0024Квантование в разделе Quantize a Signal не требует никакого априорного знания о переданном сигнале. На практике можно часто высказывать образованные предположения о существующем сигнале на основе прошлых передач сигнала. Используя такие образованные предположения, чтобы помочь квантовать сигнал известен как прогнозирующее квантование. Наиболее распространенный прогнозирующий метод квантования является дифференциальной импульсной модуляцией кода (DPCM).
Функции dpcmenco, dpcmdeco, и dpcmopt может помочь вам реализовать прогнозирующий квантизатор DPCM с линейным предиктором.
Чтобы определить энкодер для такого квантизатора, необходимо предоставить не, только раздел и книга шифров как описано в Представляют Разделы и Представляют Книги шифров, но также и предиктор. Предиктор является функцией, что использование энкодера DPCM, чтобы произвести образованное предполагает каждый шаг. Линейный предиктор имеет форму
y(k) = p(1)x(k-1) + p(2)x(k-2) + ... + p(m-1)x(k-m+1) + p(m)x(k-m)
где x является исходным сигналом, y(k) попытки предсказать значение x(k), и p m- кортеж вещественных чисел. Вместо того, чтобы квантовать x самостоятельно, энкодер DPCM квантует прогнозирующую ошибку, x-y. Целочисленный m выше называется прогнозирующим порядком. Особый случай, когда m = 1 называется модуляцией дельты.
Если предположение для kзначение th x сигнала, на основе более ранних значений x,
y(k) = p(1)x(k-1) + p(2)x(k-2) +...+ p(m-1)x(k-m+1) + p(m)x(k-m)
затем соответствующий вектор предиктора для функций тулбокса
predictor = [0, p(1), p(2), p(3),..., p(m-1), p(m)]
Примечание
Начальный нуль в векторе предиктора целесообразен, если вы просматриваете вектор как полиномиальную передаточную функцию фильтра конечной импульсной характеристики (FIR).
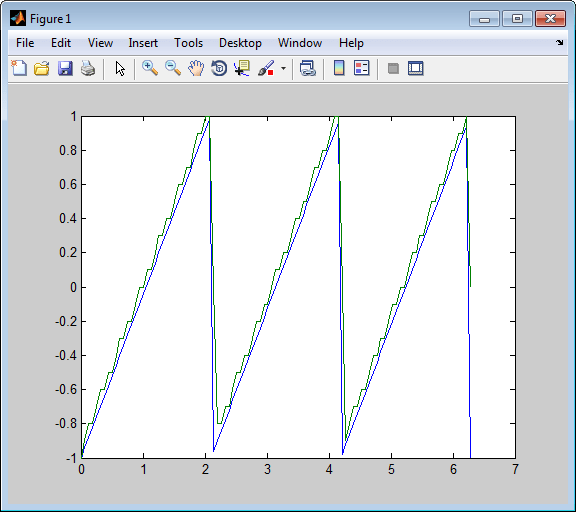
Простой особый случай DPCM квантует различие между текущим значением сигнала и его значением на предыдущем шаге. Таким образом предиктором является только y(k) = x (k - 1). Код ниже реализует эту схему. Это кодирует пилообразное сообщение, декодирует его и строит обоих исходные и декодируемые сигналы. Сплошная линия является исходным сигналом, в то время как пунктирная линия является восстановленными сигналами. Пример также вычисляет среднеквадратичную погрешность между исходными и декодируемыми сигналами.
predictor = [0 1]; % y(k)=x(k-1) partition = [-1:.1:.9]; codebook = [-1:.1:1]; t = [0:pi/50:2*pi]; x = sawtooth(3*t); % Original signal % Quantize x using DPCM. encodedx = dpcmenco(x,codebook,partition,predictor); % Try to recover x from the modulated signal. decodedx = dpcmdeco(encodedx,codebook,predictor); plot(t,x,t,decodedx,'--') legend('Original signal','Decoded signal','Location','NorthOutside'); distor = sum((x-decodedx).^2)/length(x) % Mean square error
Выход
distor =
0.0327
Раздел Optimize Quantization Parameters описывает, как использовать обучающие данные с lloyds функционируйте, чтобы помочь найти параметры квантования, которые минимизируют искажение сигнала.
В этом разделе описываются подобные процедуры для использования dpcmopt функция в сочетании с двумя функциями dpcmenco и dpcmdeco, которые сначала появляются в предыдущем разделе.
Примечание
Обучающие данные вы используете с dpcmopt должно быть типично для видов сигналов, с которыми вы будете на самом деле квантовать dpcmenco.
Этот пример похож на тот в последнем разделе. Однако, где последний пример создал predictorраздел, и codebook прямым, но случайным способом этот пример использует ту же книгу шифров (теперь названный initcodebook) как исходное предположение для нового оптимизированного параметра книги шифров. Этот пример также использует прогнозирующий порядок, 1, как желаемый порядок нового оптимизированного предиктора. dpcmopt функция создает эти оптимизированные параметры, с помощью пилообразного x сигнала как обучающие данные. Пример продолжает квантовать обучающие данные сам; в теории оптимизированные параметры подходят для квантования других данных, которые похожи на x. Заметьте, что среднеквадратическое искажение здесь очень меньше искажения в предыдущем примере.
t = [0:pi/50:2*pi]; x = sawtooth(3*t); % Original signal initcodebook = [-1:.1:1]; % Initial guess at codebook % Optimize parameters, using initial codebook and order 1. [predictor,codebook,partition] = dpcmopt(x,1,initcodebook); % Quantize x using DPCM. encodedx = dpcmenco(x,codebook,partition,predictor); % Try to recover x from the modulated signal. decodedx = dpcmdeco(encodedx,codebook,predictor); distor = sum((x-decodedx).^2)/length(x) % Mean square error
Выход
distor =
0.0063
Сожмите и расширьте последовательность данных Используя Mu-закон
Сожмите и расширьте последовательность данных Используя A-закон
В определенных приложениях, таких как речевая обработка, распространено использовать расчет логарифма, названный компрессором, перед квантованием. Обратная работа компрессора называется расширителем. Комбинация компрессора и расширителя называется компандером.
Для получения дополнительной информации смотрите quantiz и compand.
Сгенерируйте последовательность данных.
data = 2:2:12
data = 1×6
2 4 6 8 10 12
Сожмите последовательность данных при помощи компрессора mu-закона. Установите значение для mu к 255. Сжатая последовательность данных теперь располагается между 8,1 и 12.
compressed = compand(data,255,max(data),'mu/compressor')compressed = 1×6
8.1644 9.6394 10.5084 11.1268 11.6071 12.0000
Расширьте сжатую последовательность данных при помощи расширителя mu-закона. Расширенная последовательность данных почти идентична исходной последовательности данных.
expanded = compand(compressed,255,max(data),'mu/expander')expanded = 1×6
2.0000 4.0000 6.0000 8.0000 10.0000 12.0000
Вычислите разность между исходной последовательностью данных и расширенной последовательностью.
diffvalue = expanded - data
diffvalue = 1×6
10-14 ×
-0.0444 0.1776 0.0888 0.1776 0.1776 -0.3553
Сгенерируйте последовательность данных.
data = 1:5;
Сожмите последовательность данных при помощи компрессора A-закона. Установите значение для к 87,6. Сжатая последовательность данных теперь располагается между 3,5 и 5.
compressed = compand(data,87.6,max(data),'A/compressor')compressed = 1×5
3.5296 4.1629 4.5333 4.7961 5.0000
Расширьте сжатую последовательность данных при помощи расширителя A-закона. Расширенная последовательность данных почти идентична исходной последовательности данных.
expanded = compand(compressed,87.6,max(data),'A/expander')expanded = 1×5
1.0000 2.0000 3.0000 4.0000 5.0000
Вычислите разность между исходной последовательностью данных и расширенной последовательностью.
diffvalue = expanded - data
diffvalue = 1×5
10-14 ×
0 0 0.1332 0.0888 0.0888
Кодирование методом Хаффмана предлагает способ сжать данные. Средняя длина Кода Хаффмана зависит от статистической частоты, с которой источник производит каждый символ из своего алфавита. Словарь Кода Хаффмана, который сопоставляет каждый символ данных с кодовой комбинацией, имеет свойство, что никакая кодовая комбинация в словаре не является префиксом никакой другой кодовой комбинации в словаре.
huffmandict, huffmanenco, и huffmandeco функции поддерживают Кодирование методом Хаффмана и декодирование.
Примечание
Для длинных последовательностей из источников, скашивавших распределения и маленькие алфавиты, кодирование арифметики сжимается лучше, чем Кодирование методом Хаффмана. Чтобы изучить, как использовать арифметическое кодирование, смотрите Арифметическое Кодирование.
Кодирование методом Хаффмана запрашивает статистическую информацию об источнике закодированных данных. В частности, p входной параметр в huffmandict функционируйте перечисляет вероятность, с которой источник производит каждый символ в своем алфавите.
Например, рассмотрите источник данных, который производит 1 с с вероятностью 0.1, 2 с с вероятностью 0.1 и 3 с с вероятностью 0.8. Основной вычислительный шаг в кодировании данных из этого источника с помощью Кода Хаффмана должен создать словарь, который сопоставляет каждый символ данных с кодовой комбинацией. Пример здесь создает такой словарь и затем показывает вектор кодовой комбинации, сопоставленный с особым значением от источника данных.
В этом примере показано, как создать словарь Кода Хаффмана с помощью huffmandict функция.
Создайте вектор из символов данных и определите вероятность каждому.
symbols = [1 2 3]; prob = [0.1 0.1 0.8];
Создайте словарь Кода Хаффмана. Самый вероятный символ данных, 3, сопоставлен с одноразрядной кодовой комбинацией, в то время как менее вероятные символы данных сопоставлены с кодовыми комбинациями 2D цифры.
dict = huffmandict(symbols,prob)
dict=3×2 cell array
{[1]} {[1 1]}
{[2]} {[1 0]}
{[3]} {[ 0]}
Отобразите вторую строку словаря. Выход также показывает что энкодер Хафмана, получающий символ данных 2 заменяет последовательностью 1 0.
dict{2,:}ans = 2
ans = 1×2
1 0
Пример выполняет Кодирование методом Хаффмана и декодирующий использование источника, алфавит которого имеет три символа. Заметьте, что huffmanenco и huffmandeco функции используют словарь, созданный huffmandict.
Сгенерируйте последовательность данных, чтобы закодировать.
sig = repmat([3 3 1 3 3 3 3 3 2 3],1,50);
Задайте набор символов данных и вероятности, сопоставленной с каждым элементом.
symbols = [1 2 3]; p = [0.1 0.1 0.8];
Создайте словарь Кода Хаффмана.
dict = huffmandict(symbols,p);
Закодируйте и декодируйте данные. Проверьте что исходные данные, sig, и декодируемые данные, dhsig, идентичны.
hcode = huffmanenco(sig,dict); dhsig = huffmandeco(hcode,dict); isequal(sig,dhsig)
ans = logical
1
Кодирование арифметики предлагает способ сжать данные и может быть полезно для источников данных, имеющих маленький алфавит. Длина арифметического кода, вместо того, чтобы быть зафиксированной относительно количества закодированных символов, зависит от статистической частоты, с которой источник производит каждый символ из своего алфавита. Для длинных последовательностей из источников, скашивавших распределения и маленькие алфавиты, кодирование арифметики сжимается лучше, чем Кодирование методом Хаффмана.
arithenco и arithdeco функции поддерживают арифметическое кодирование и декодирование.
Арифметическое кодирование запрашивает статистическую информацию об источнике закодированных данных. В частности, counts входной параметр в arithenco и arithdeco функции перечисляют частоту, с которой источник производит каждый символ в своем алфавите. Можно определить частоты путем изучения набора тестовых данных из источника. Набор тестовых данных может иметь любой размер, который вы выбираете, пока каждый символ в алфавите имеет ненулевую частоту.
Например, прежде, чем закодировать данные из источника, который производит 10 x's, 10 лет и 80 z's в типичном 100 наборах символов тестовых данных, задают
counts = [10 10 80];
В качестве альтернативы, если больший набор тестовых данных из источника содержит 22 x's, 23 года и 185 z's, то задают
counts = [22 23 185];
Закодируйте и декодируйте последовательность из источника, имеющего три символа.
Создайте вектор последовательности, содержащий символы от набора {1,2,3}.
seq = [3 3 1 3 3 3 3 3 2 3];
Установите counts вектор, чтобы задать энкодер, который производит 10 единиц, 20 пар и 70 троек от типичного 100 наборов символов тестовых данных.
counts = [10 20 70];
Примените арифметические функции энкодера и декодера.
code = arithenco(seq,counts); dseq = arithdeco(code,counts,length(seq));
Проверьте, что декодер выводил соответствия исходная входная последовательность.
isequal(seq,dseq)
ans = logical
1
Код ниже показов, как quantiz функционируйте использует partition и codebook сопоставлять вектор действительных чисел, samp, к новому вектору, quantized, чьи записи или-1, 0.5, 2, или 3.
partition = [0,1,3]; codebook = [-1, 0.5, 2, 3]; samp = [-2.4, -1, -.2, 0, .2, 1, 1.2, 1.9, 2, 2.9, 3, 3.5, 5]; [index,quantized] = quantiz(samp,partition,codebook); quantized
Выход ниже.
quantized =
Columns 1 through 6
-1.0000 -1.0000 -1.0000 -1.0000 0.5000 0.5000
Columns 7 through 12
2.0000 2.0000 2.0000 2.0000 2.0000 3.0000
Column 13
3.0000
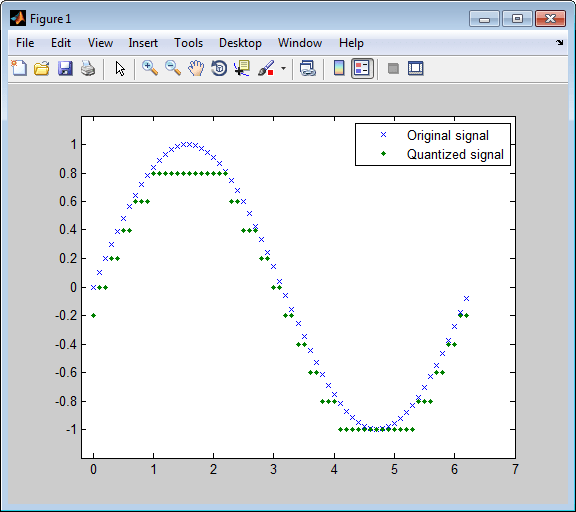
Этот пример иллюстрирует природу скалярного квантования более ясно. После квантования произведенной синусоиды это строит исходные и квантованные сигналы. График контрастирует xэто составляет синусоиду с точками, которые составляют квантованный сигнал. Вертикальная координата каждой точки является значением в векторном codebook.
t = [0:.1:2*pi]; % Times at which to sample the sine function sig = sin(t); % Original signal, a sine wave partition = [-1:.2:1]; % Length 11, to represent 12 intervals codebook = [-1.2:.2:1]; % Length 12, one entry for each interval [index,quants] = quantiz(sig,partition,codebook); % Quantize. plot(t,sig,'x',t,quants,'.') legend('Original signal','Quantized signal'); axis([-.2 7 -1.2 1.2])