Диаграмма нулей и полюсов динамической системы
pzmap( создает диаграмму нулей и полюсов модели
sys)sys динамической системы непрерывного или дискретного времениX и o указывает на полюса и нули соответственно, как показано в следующем рисунке.
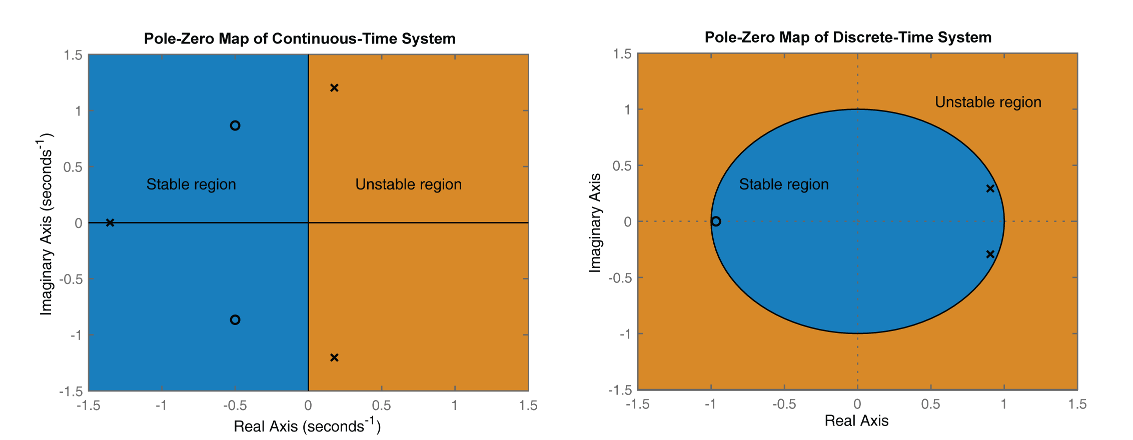
От фигуры выше, разомкнутый контур линейная независимая от времени система устойчива если:
В непрерывное время все полюса на комплексной s-плоскости должны быть в левой полуплоскости (синяя область), чтобы гарантировать устойчивость. Система незначительно устойчива, если отличные полюса лежат на мнимой оси, то есть, действительные части полюсов являются нулем.
В дискретное время все полюса в комплексной z-плоскости должны лечь в модульном кругу (синяя область). Система незначительно устойчива, если она имеет один или несколько полюсов, лежащих на модульном круге.
pzmap( создает диаграмму нулей и полюсов многоуровневых моделей на одной фигуре. Модели могут иметь различные количества вводов и выводов и могут быть соединением непрерывных и дискретных систем. Для систем SISO, sys1,sys2,...,sysN)pzmap строит системные полюса и нули. Для систем MIMO, pzmap строит системные полюса и нули передачи.
Используйте функции sgrid или zgrid к сюжетным линиям постоянного коэффициента затухания и собственной частоты в s - или z - плоскость на диаграмме нулей и полюсов.
Для моделей MIMO, pzmap отображения все системные полюса и нули передачи на одном графике. Чтобы сопоставить полюса и нули для отдельных пар ввода-вывода, использовать iopzmap.
Для дополнительных опций настроить внешний вид диаграммы нулей и полюсов, использовать pzplot.