Движение платформы модели Используя объекты траектории

Эта тема вводит, как использовать три различных объекта траектории смоделировать траектории платформы, и как выбрать между ними.

Введение

Sensor Fusion and Tracking Toolbox™ обеспечивает три Системных объекта, которые можно использовать для траекторий модели платформ включая наземные транспортные средства, поставки, самолет и космический корабль. Можно выбрать между этими объектами траектории на основе доступной информации о траектории и промежутка расстояния траектории.

waypointTrajectory — Задает траекторию с помощью нескольких waypoints в Декартовых координатах, через которые должна пройти траектория. Траектория принимает, что система координат является фиксированным Северо-востоком вниз (NED) или системой координат "восточного севера" (ENU). Поскольку интерполяция траектории принимает, что гравитационное ускорение, описанное в системе координат траектории, является постоянным, waypointTrajectory обычно используется для траектории, заданной в области, которая охватывает только десятки или сотни километров.
geoTrajectory — Задает траекторию с помощью нескольких waypoints в геодезических координатах (широта, долгота и высота), через который должна пройти траектория. Поскольку waypoints описываются в геодезических координатах, geoTrajectory обычно используется для траектории от сотен до тысяч километров промежутка расстояния.
kinematicTrajectory — Задает траекторию с помощью кинематических свойств, таких как ускорение и угловое ускорение, описанное в системе координат тела платформы. Можно использовать kinematicTrajectory чтобы сгенерировать траекторию любого промежутка расстояния пока, кинематическая информация траектории доступна. Объект принимает систему координат Декартовой координаты.

Два находящихся в waypoint объекта траектории (waypointTrajectory и geoTrajectory) может автоматически вычислить линейную информацию о скорости платформы, но можно также явным образом задать линейную скорость с помощью Velocity свойство или комбинация Course, GroundSpeed, и ClimbRate свойства.

Траектория платформы состоит из вращательного движения и поступательного движения. По умолчанию, два находящихся в waypoint объекта траектории (waypointTrajectory и geoTrajectory) автоматически сгенерируйте ориентацию платформы в каждом waypoint путем выравнивания угла рыскания с путем траектории, но можно явным образом задать ориентацию с помощью Orientation свойство. Альтернативно, можно использовать AutoPitch и AutoBank свойства включить автоматические углы продольного и поперечного крена, соответственно. Для kinematicTrajectory, необходимо использовать Orientation свойство и вход скорости вращения, чтобы задать вращательное движение траектории.

`waypointTrajectory`

waypointTrajectory Системный объект задает траекторию, которая гладко проходит через waypoints, описанный в Декартовых координатах. Обычно можно использовать waypointTrajectory к транспортным средствам модели, перемещающимся в сотнях километров. Эти транспортные средства включают автомобили, появляются морское ремесло и коммерческий самолет (вертолеты, плоскости и quadcopters). Можно выбрать систему координат в качестве фиксированного ENU или системы координат NED с помощью ReferenceFrame свойство. Для получения дополнительной информации о том, как объект генерирует траекторию, смотрите раздел Algorithms waypointTrajectory.

`waypointTrajectory` Пример для приземления самолета

Скрипт Open Live Script

Задайте траекторию приземляющегося самолета с помощью waypointTrajectory объект.

waypoints = [-421 -384 2000;
    47 -294 1600;
    1368 174 1300;
    995 1037 900;
    -285 293 600;
    -1274 84 350;
    -2328 101 150;
    -3209 83 0];
timeOfArrival =  [0; 16.71; 76.00; 121.8; 204.3; 280.31; 404.33; 624.6];
aircraftTraj = waypointTrajectory(waypoints,timeOfArrival);

Создайте theaterPlot объект визуализировать траекторию и самолет.

minCoords = min(waypoints);
maxCoords = max(waypoints);
tp = theaterPlot('XLimits',1.2*[minCoords(1) maxCoords(1)], ...
    'YLimits',1.2*[minCoords(2) maxCoords(2)], ...
    'ZLimits',1.2*[minCoords(3) maxCoords(3)]);

% Create a trajectory plotter and a platform plotter
tPlotter = trajectoryPlotter(tp,'DisplayName','Trajectory');
pPlotter = platformPlotter(tp,'DisplayName','Aircraft');

Получите Декартов waypoints траектории с помощью lookupPose объектная функция.

sampleTimes = timeOfArrival(1):timeOfArrival(end);
numSteps = length(sampleTimes);
[positions,orientations] = lookupPose(aircraftTraj,sampleTimes);
plotTrajectory(tPlotter,{positions})
axis equal

Постройте движение платформы с помощью объекта ячейки самолета.

mesh = scale(rotate(tracking.scenario.airplaneMesh,[0 0 180]),15); % Exaggerated scale for better visualization
view(20.545,-20.6978)
for i = 1:numSteps
    plotPlatform(pPlotter,positions(i,:),mesh,orientations(i))
    % Uncomment the next line to slow the aircraft motion animation
    % pause(1e-7)
end

В анимации угол рыскания самолета выравнивается с траекторией по умолчанию.

Создайте вторую траекторию самолета с тем же waypoints как первая траектория самолета, но установите ее AutoPitch и AutoBank свойства к true. Это генерирует траекторию, более представительную для возможных маневров самолета.

aircraftTraj2 = waypointTrajectory(waypoints,timeOfArrival, ...
    'AutoPitch',true, ...
    'AutoBank',true);

Постройте вторую траекторию и наблюдайте изменение в ориентации самолета.

[positions2,orientations2] = lookupPose(aircraftTraj2,sampleTimes);
for i = 1:numSteps
    plotPlatform(pPlotter,positions2(i,:),mesh,orientations2(i));
    % Uncomment the next line to slow the aircraft motion animation
    % pause(1e-7)
end

Figure contains an axes. The axes contains 2 objects of type line. These objects represent Trajectory, Aircraft.

Визуализируйте различия в ориентации между этими двумя траекториями в углах.

distance = dist(orientations2,orientations);
figure
plot(sampleTimes,distance*180/pi)
xlabel('Time (sec)')
ylabel('Angular Ditance (dge)')
title('Orientation Difference Between Two Waypoint Trajectories')

Figure contains an axes. The axes with title Orientation Difference Between Two Waypoint Trajectories contains an object of type line.

`geoTrajectory`

geoTrajectory Системный объект генерирует траекторию с помощью waypoints подобным способом как waypointTrajectory объект, но это имеет два существенных различия в том, как задать скоростные входные параметры и waypoints.

При определении waypoints для geoTrajectory, опишите каждый waypoint в геодезических координатах широты, долготы и высоты выше модели эллипсоида WG84. Используя геодезические координаты, можно удобно задать траектории дальние, такие как траектория рейса самолета на реалистической модели Earth.
При определении ориентации и информации о скорости для каждого waypoint, система координат для ориентации и скорости является локальным NED или системой координат ENU, заданной под текущей траекторией waypoint. Например, показанная на рисунке система координат _1-E1-D1 N является локальной системой координат NED.

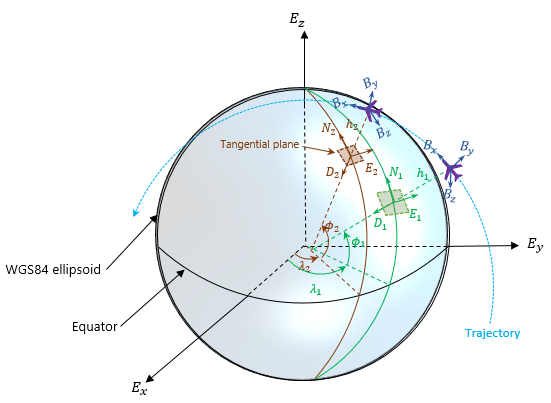
На рисунке,

_x E, E _y и E_{, z} является тремя осями системы координат Сосредоточенного землей зафиксированного землей (ECEF), которая закрепляется на Земле.
(λ ₁, ϕ ₁, h ₁), и (λ ₂, ϕ ₂, h ₂) геодезические координаты плоскости в двух waypoints.
(N ₁, E ₁, D ₁), и (N ₂, E ₂, D ₂) две локальных системы координат NED, соответствующие двум траекториям waypoints.
_x B, B _y и B_{, z}является тремя осями системы координат тела платформы, которая закрепляется на платформе.

geo`Trajectory` Пример для траектории рейса

Скрипт Open Live Script

Загрузите полетные данные траектории рейса от Лос-Анджелеса до Бостона. Данные содержат информацию о рейсе включая время полета, геодезические координаты для каждого waypoint, курса и скорости относительно земли.

load flightData.mat

Создайте geoTrajectory основанный на объектах на полетных данных.

planeTraj = geoTrajectory([latitudes longitudes heights],timeOfArrival, ...
    'Course',courses,'GroundSpeed',speeds);

Ищите Декартовы координаты waypoints в системе координат ECEF.

sampleTimes = 0:1000:3600*10;
positionsCart = lookupPose(planeTraj,sampleTimes,'ECEF');

Покажите траекторию с помощью helperGlobeView класс, который аппроксимирует Наземную сферу.

viewer = helperGlobeView;
plot3(positionsCart(:,1),positionsCart(:,2),positionsCart(:,3),'r')

Можно далее исследовать траекторию путем запроса других выходных параметров траектории.

`kinematicTrajectory`

В отличие от двух waypoint объектов траектории, kinematicTrajectory Системный объект использует кинематические атрибуты, чтобы задать траекторию. Думайте о траектории как о численном интегрировании положения (положение и ориентация) и линейная скорость платформы, на основе линейного ускорения и угловой информации об ускорении. Положение и линейная скорость заданы с уважаемым выбранной, зафиксированной системе координат сценария, тогда как линейное ускорение и скорость вращения заданы с уважаемым системе координат тела платформы.

`kinematicTrajectory` Пример для пути UAV

Скрипт Open Live Script

Создайте kinematicTrajectory объект для симуляции пути UAV. Задайте отрезок времени траектории как 120 секунд.

traj = kinematicTrajectory('SampleRate',1, ...
    'AngularVelocitySource','Property');

tStart = 0;
tFinal = 120;
tspan = tStart:tFinal;

numSteps = length(tspan);
positions = NaN(3,numSteps);
velocities = NaN(3,numSteps);
vel = NaN(1,numSteps);

Чтобы сформировать квадратный путь, покрывающий небольшую область, разделите траекторию UAV на шесть сегментов:

Взлетание и возрастание в z-направлении
Перемещение в положительное направление X
Перемещение в положительное направление Y
Перемещение в отрицательное направление X
Перемещение в отрицательное направление Y
Убывание в z-направлении и приземлении

В каждом сегменте UAV ускоряется в одном направлении и затем замедляется в том направлении с той же ускоряющей величиной. В результате в конце каждого сегмента, скорость UAV является нулем.

segSteps = floor(numSteps/12);
accelerations = zeros(3,numSteps);
acc = 1;
% Acceleration for taking off and ascending in the z-direction
accelerations(3,1:segSteps) = acc;
accelerations(3,segSteps+1:2*segSteps) = -acc;

% Acceleration for moving in the positive x-direction
accelerations(1,2*segSteps+1:3*segSteps) = acc;
accelerations(1,3*segSteps+1:4*segSteps) = -acc;

% Acceleration for moving in the positive y-direction
accelerations(2,4*segSteps+1:5*segSteps) = acc;
accelerations(2,5*segSteps+1:6*segSteps) = -acc;

% Acceleration for moving in the negative x-direction
accelerations(1,6*segSteps+1:7*segSteps) = -acc;
accelerations(1,7*segSteps+1:8*segSteps) = acc;

% Acceleration for moving in the negative y-direction 
accelerations(2,8*segSteps+1:9*segSteps) = -acc;
accelerations(2,9*segSteps+1:10*segSteps) = acc;

% Descending in the z-direction and landing
accelerations(3,10*segSteps+1:11*segSteps) =-acc;
accelerations(3,11*segSteps+1:end) = acc;

Симулируйте траекторию путем вызова kinematicTrajectory объект с заданным ускорением.

for i = 1:numSteps
    [positions(:,i),~,velocities(:,i)] = traj(accelerations(:,i)');  
     vel(i) = norm(velocities(:,i));
end

Визуализируйте траекторию с помощью theaterPlot.

% Create a theaterPlot object and create plotters for the trajectory and the
% UAV Platform.
figure
tp = theaterPlot('XLimits',[-30 130],'YLimits',[-30 130],'ZLimits',[-30 130]);
tPlotter = trajectoryPlotter(tp,'DisplayName','UAV trajectory');
pPlotter = platformPlotter(tp,'DisplayName','UAV','MarkerFaceColor','g');

% Plot the trajectory.
plotTrajectory(tPlotter,{positions'})
view(-43.18,56.49)

% Use a cube to represent the UAV platform.
dims = struct('Length',10, ...
    'Width',5, ...
    'Height',3, ...
    'OriginOffset',[0 0 0]);

% Animate the UAV platform position.
for i = 1:numSteps
    plotPlatform(pPlotter,positions(:,i)',dims,eye(3))
    pause(0.01)
end

Figure contains an axes. The axes contains 2 objects of type line. These objects represent UAV trajectory, UAV.

Покажите величину скорости платформы UAV.

figure
plot(tspan,vel)
xlabel('Time (s)')
ylabel('Velocity (m/s)')
title('Magnitude of the UAV Velocity')

Figure contains an axes. The axes with title Magnitude of the UAV Velocity contains an object of type line.

`kinematicTrajectory` Пример для относящейся к космическому кораблю траектории

Скрипт Open Live Script

Используйте kinematicTrajetory задавать круговую относящуюся к космическому кораблю траекторию. Орбита имеет эти элементы:

Орбитальный радиус ( $r$ ) — 7 000 км
Наклон ( $i$ ) — 60 градусов
Аргумент возрастающего узла ( $Ω$ ) — 90 градусов. Возрастающее направление узла выравнивается с $Y$ - направление.
Истинная аномалия ( $ν$ ) — –90 градусов

На рисунке, $X$ - $Y$ - $Z$ система координат Сосредоточенного землей инерционного (ECI), которая имеет фиксированную позицию и ориентацию на пробеле. $x$ - $y$ - $z$ относящаяся к космическому кораблю система координат тела, закрепленная на космическом корабле. $\vec{r}$ и $\vec{v}$ исходное положение и скорость космического корабля.

Задавать круговую орбиту с помощью kinematicTrajectory, необходимо обеспечить исходное положение, начальную скорость и начальную ориентацию космического корабля относительно системы координат ECI. Для выбранной истинной аномалии ( $v$ = – $90^{\circ}$ ), относящаяся к космическому кораблю скорость выравнивается с $Y$ - направление.

inclination = 60; % degrees
mu = 3.986e14; % standard earth gravitational parameter
radius = 7000e3;% meters
v = sqrt(mu/radius); % speed
initialPosition = [radius*cosd(inclination),0,-radius*sind(inclination)]';
initialVelocity = [0 v 0]';

Примите, что направление X относящейся к космическому кораблю системы координат тела является радиальным направлением, z-направление является нормальным направлением орбитальной плоскости, и направление Y завершает правило правой руки. Используйте предположения, чтобы задать ориентацию системы координат тела в исходном положении.

orientation = quaternion([0 inclination 0],'eulerd','zyx','frame');

Опишите скорость вращения и угловое ускорение траектории в системе координат тела платформы.

omega = v/radius;
angularVelocity = [0 0 omega]';
a = v^2/radius;
acceleration = [-a 0 0]';

Установите время симуляции одного орбитального периода. Задайте шаг симуляции как 2 секунды.

tFinal = 2*pi/omega;
dt = 2;
sampleRate = 1/dt;
tspan = 0:dt:tFinal;
numSteps = length(tspan);

Создайте относящуюся к космическому кораблю траекторию. Поскольку ускорение и скорость вращения космического корабля остаются постоянными относительно относящейся к космическому кораблю системы координат тела, задают их как константы. Сгенерируйте положение и ориентацию выходные параметры вдоль траектории при помощи kinematicTrajectory объект.

traj = kinematicTrajectory('SampleRate',sampleRate, ...
    'Position',initialPosition, ...
    'Velocity',initialVelocity, ...
    'Orientation',orientation, ...
    'AngularVelocity',angularVelocity, ...
    'Acceleration',acceleration, ...
    'AccelerationSource','Property', ...
    'AngularVelocitySource','Property');

% Generate position and orientation outputs.
positions = NaN(3,numSteps);
orientations = zeros(numSteps,1,'quaternion');
for i = 1:numSteps    
   [positions(:,i),orientations(i)] = traj();     
end

Используйте helperGlobeView класс и theaterPlot показать траекторию.

viewer = helperGlobeView(0,[60 0]);
tp = theaterPlot('Parent',gca,...
    'XLimits',1.2*[-radius radius],...
    'YLimits',1.2*[-radius radius],...
    'ZLimits',1.2*[-radius radius]);
tPlotter = trajectoryPlotter(tp,'LineWidth',2);
pPlotter = platformPlotter(tp,'MarkerFaceColor','m');
legend(gca,'off')

plotTrajectory(tPlotter,{positions'})
% Use a cube with exaggerated dimensions to represent the spacecraft.
dims = struct('Length',8e5,'Width',4e5,'Height',2e5,'OriginOffset',[0 0 0]);

for i = 1:numSteps    
   plotPlatform(pPlotter,positions(:,i)',dims,orientations(i))
   % Since the reference frame is the ECI frame, earth rotates with respect to it.
   rotate(viewer,dt)
end

Сводные данные

В этой теме вы изучили, как использовать три объекта траектории настроить ваши собственные траектории на основе доступной информации. Кроме того, вы изучили принципиальные различия в применении их. Эта таблица подсвечивает основные атрибуты этих объектов траектории.

Объект траектории	Входные параметры положения	Линейные скоростные входные параметры	Ориентация	Ускорение и входные параметры скорости вращения	Рекомендуемый промежуток расстояния
`waypointTrajectory`	Декартов waypoints описывается в фиксированной системе координат (NED или ENU)	Одна из этих опций: Автоматически сгенерируйте скорость для сглаженной траектории по умолчанию Задайте скорость в фиксированной системе координат в каждом waypoint Задайте курс, скорость относительно земли и скороподъемность в фиксированной системе координат в каждом waypoint	Одна из этих опций: Автоматическое рыскание по умолчанию, автоматический тангаж выбором и автоматический банк выбором Задайте ориентацию в фиксированной системе координат	Не может задать	Из десятков к сотням километров
`geoTrajectory`	Геодезический waypoints в системе координат ECEF	Одна из этих опций: Автоматически сгенерируйте скорость для сглаженной траектории по умолчанию Задайте скорость в локальной системе координат (NED или ENU) для каждого waypoint Задайте курс, скорость относительно земли и скороподъемность в локальной системе координат (NED или ENU) для каждого waypoint	Одна из этих опций: Автоматическое рыскание по умолчанию, автоматический тангаж выбором и автоматический банк выбором Задайте ориентацию в локальной системе координат	Не может задать	От сотен до тысяч километров
`kinematicTrajectory`	Исходная позиция выражена в выбранной, зафиксированной системе координат	Только начальная скорость в фиксированной системе координат	Только начальная ориентация в фиксированной системе координат	Задайте ускорение и скорость вращения в системе координат тела платформы	Неограниченный промежуток расстояния

Документация