Нелинейные модели ARX расширяют линейные модели ARX к нелинейному случаю. Структура этих моделей позволяет вам смоделировать комплексное нелинейное поведение с помощью гибких нелинейных функций, таких как вейвлет и сигмоидальные сети. Для получения информации о том, когда подбирать нелинейные модели, займитесь Идентифицированными Нелинейными Моделями.
Линейная модель SISO ARX имеет следующую структуру:
Где, u, y и e являются входом, выходом и шумом. Эта структура подразумевает, что текущая производительность y (t) предсказана как взвешенная сумма прошлых выходных значений и текущих и прошлых входных значений. na является количеством прошлых выходных условий, и nb является количеством прошлых входных терминов, использованных, чтобы предсказать текущую производительность. Входная задержка nk обнуляется, чтобы упростить обозначение. При перезаписи уравнения, когда продукт дает:
где задержанные переменные ввода и вывода, названные регрессорами. Содействующий вектор [–a1, ... ,bnb] представляет взвешивание, применился к этим регрессорам. Линейная модель ARX таким образом предсказывает текущую производительность yp как взвешенная сумма его регрессоров.
Структура нелинейной модели ARX позволяет следующую дополнительную гибкость:
Вместо взвешенной суммы регрессоров, которая представляет линейное отображение, нелинейная модель ARX имеет более гибкую нелинейную функцию отображения, F.
Входные параметры к F являются регрессорами модели. Когда вы задаете нелинейную структуру модели ARX, можно выбрать одну из нескольких доступных нелинейных функций. Например, F может представлять взвешенную сумму вейвлетов, которые работают с расстоянием регрессоров от их средних значений. Для получения дополнительной информации смотрите Доступные Функции Отображения для Нелинейных Моделей ARX.
Нелинейные регрессоры ARX могут быть и задержанными переменными ввода - вывода и более комплексными, нелинейными выражениями задержанных переменных ввода и вывода. Примерами таких нелинейных регрессоров является y (t-1) 2, u (t-1) *y (t-2), abs (u (t-1)), и макс. (u (t-1) *y (t-3),-10).
Нелинейная модель ARX состоит из регрессоров модели и выходной функции. Выходная функция включает линейные и нелинейные функции, которые действуют на регрессоры модели, чтобы дать выход модели и фиксированное смещение для того выхода. Эта блок-схема представляет структуру нелинейной модели ARX в сценарии симуляции.
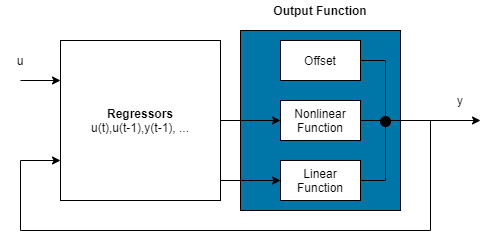
Программное обеспечение вычисляет нелинейную модель ARX выход y на двух этапах:
Это вычисляет значения регрессора из текущих и прошлых входных значений и прошлых выходных данных.
В самом простом случае регрессоры являются задержанными вводами и выводами, такими как u (t –1) и y (t –3). Подобные регрессоры называются linear regressors. Вы задаете линейные регрессоры с помощью linearRegressor объект. Можно также задать линейные регрессоры при помощи линейных порядков модели ARX как входной параметр. Для получения дополнительной информации смотрите Нелинейные Порядки Модели ARX и Задержку. Однако этот второй подход ограничивает ваш набор регрессора к линейным регрессорам с последовательными задержками. Чтобы создать polynomial regressors, используйте polynomialRegressor объект. Можно также задать custom regressors, которые являются нелинейными функциями задержанных вводов и выводов. Например, u (t –1) y (t –3) является пользовательским регрессором, который умножает экземпляры ввода и вывода вместе. Задайте пользовательские регрессоры с помощью customRegressor объект.
Можно присвоить любой из регрессоров как входные параметры с блоком линейной функции выходной функции, нелинейного функционального блока или обоих.
Это сопоставляет регрессоры с выходом модели с помощью блока выходной функции. Блок выходной функции может включать линейные и нелинейные блоки параллельно. Например, рассмотрите следующее уравнение:
Здесь, x является вектором из регрессоров, и r является средним значением x. выход блока линейной функции. представляет выход нелинейного функционального блока. Q является матрицей проекции, которая делает вычисления хорошо подготовленными. d является скалярным смещением, которое добавляется к объединенным выходным параметрам линейных и нелинейных блоков. Точная форма F (x) зависит от вашего выбора выходной функции. Можно выбрать из доступных объектов отображения, таких как сети древовидного раздела, сети вейвлета и многоуровневые нейронные сети. Можно также исключить или линейное или нелинейный функциональный блок от выходной функции.
При оценке нелинейной модели ARX программное обеспечение вычисляет значения параметра модели, такие как L, r, d, Q и другие параметры, задающие g.
Получившиеся нелинейные модели ARX idnlarx объекты, которые хранят все данные модели, включая регрессоры модели и параметры выходной функции. Для получения дополнительной информации об этих объектах, смотрите Нелинейные Структуры модели.
Как правило, вы используете нелинейные модели ARX в качестве структур черного ящика. Нелинейная функция нелинейной модели ARX является гибким средством оценки нелинейности параметрами, которые не должны иметь физического значения. Можно оценить нелинейный ARX в приложении System Identification или в командной строке с помощью nlarx команда. Можно использовать однородно произведенные данные ввода - вывода временного интервала или данные timeseries (никакие входные параметры) для оценки нелинейных моделей ARX. Ваши данные могут иметь один или несколько каналов ввода и вывода. Вы не можете использовать данные частотного диапазона для оценки.
Можно использовать порядки и задержки нелинейной модели ARX, чтобы задать линейные регрессоры модели. Порядки и задержка определяются следующим образом:
нет данных Количество прошлых выходных условий раньше предсказывало текущую производительность.
nb — Количество прошлых входных сроков раньше предсказывало текущую производительность.
nk — Задержитесь от входа до выхода в терминах количества выборок.
Значение na, nb и nk похоже на это для линейных параметров модели ARX. Порядки заданы как скаляры для данных SISO, и как ny-by-nu матрицы для данных MIMO, где ny и nu являются количеством выходных параметров и входных параметров. Если вы не уверены, какие значения использовать для порядков и задержек, можно оценить их как описано в Предварительном Шаге – Оценка Порядков Модели и Входных Задержек. Такая оценка основана на линейных моделях ARX и только обеспечивает начальное руководство. Лучшие порядки для линейной модели ARX не могут быть лучшими порядками для нелинейной модели ARX.
Программное обеспечение System Identification Toolbox™ вычисляет линейные регрессоры с помощью порядков модели и задержек. Например, предположите, что вы задаете na = 2, nb = 3, и nk = 5 для модели SISO с входом u и выходом y. Тулбокс вычисляет линейные регрессоры y (t-2), y (t-1), u( t-5), u (t-6), и u (t-7).
Вместо того, чтобы использовать порядок модели ARX задать задержки регрессора, можно также задать регрессоры непосредственно, чтобы получить более комплексное поведение. Когда вы задаете линейные регрессоры непосредственно, можно включать непоследовательные условия задержки. Можно также задать полиномиальные регрессоры и пользовательские регрессоры. Для получения дополнительной информации смотрите Оценку Нелинейные Модели ARX в Приложении и Оценке Нелинейные Модели ARX в Командной строке.