Оцените параметры нелинейной модели ARX
sys = nlarx(data,orders)
sys = nlarx(data,regressors)regressors. Используйте этот синтаксис, когда у вас есть линейные регрессоры, которые имеют непоследовательные задержки, или когда у вас также есть полиномиальные регрессоры, пользовательские регрессоры или оба.
sys = nlarx(___,output_fcn)
sys = nlarx(data,linmodel,output_fcn)
sys = nlarx(data,sys0)sys0.
Используйте этот синтаксис для:
Оцените, что параметры модели ранее создали использование idnlarx конструктор. До оценки можно сконфигурировать свойства модели с помощью записи через точку.
Обновите параметры ранее предполагаемой модели, чтобы улучшить подгонку к данным об оценке. В этом случае алгоритм оценки использует параметры sys0 как исходные предположения.
Загрузите данные об оценке.
load twotankdata;Создайте iddata объект из данных об оценке с шагом расчета 0,2 секунд.
Ts = 0.2; z = iddata(y,u,Ts);
Оцените нелинейную модель ARX с помощью порядков модели ARX задать регрессоры.
sysNL = nlarx(z,[4 4 1])
sysNL = Nonlinear ARX model with 1 output and 1 input Inputs: u1 Outputs: y1 Regressors: Linear regressors in variables y1, u1 List of all regressors Output function: Wavelet Network with 11 units Sample time: 0.2 seconds Status: Estimated using NLARX on time domain data "z". Fit to estimation data: 96.84% (prediction focus) FPE: 3.482e-05, MSE: 3.431e-05
sys использует wavenet по умолчанию функционируйте как выходную функцию.
Для сравнения вычислите линейную модель ARX с теми же порядками модели.
sysL = arx(z,[4 4 1]);
Сравните выходные параметры модели с исходными данными.
compare(z,sysNL,sysL)

Нелинейная модель имеет намного лучшую подгонку к данным, чем линейная модель.
Задайте линейный регрессор, который эквивалентен матрице порядка модели ARX [4 4 1].
Матрица порядка [4 4 1] указывает, что оба набора регрессора ввода и вывода содержат четыре регрессора с задержками в пределах от 1 - 4. Например, представляет второй входной регрессор.
Задайте выход и введите имена.
output_name = 'y1'; input_name = 'u1'; names = {output_name,input_name};
Задайте выход и введите задержки.
output_lag = [1 2 3 4];
input_lag = [1 2 3 4];
lags = {output_lag,input_lag};Создайте линейный объект регрессора.
lreg = linearRegressor(names,lags)
lreg =
Linear regressors in variables y1, u1
Variables: {'y1' 'u1'}
Lags: {[1 2 3 4] [1 2 3 4]}
UseAbsolute: [0 0]
TimeVariable: 't'
Regressors described by this set
Загрузите данные об оценке и создайте объект iddata.
load twotankdata
z = iddata(y,u,0.2);Оцените нелинейную модель ARX.
sys = nlarx(z,lreg)
sys = Nonlinear ARX model with 1 output and 1 input Inputs: u1 Outputs: y1 Regressors: Linear regressors in variables y1, u1 List of all regressors Output function: Wavelet Network with 11 units Sample time: 0.2 seconds Status: Estimated using NLARX on time domain data "z". Fit to estimation data: 96.84% (prediction focus) FPE: 3.482e-05, MSE: 3.431e-05
Просмотрите регрессоры
getreg(sys)
ans = 8×1 cell
{'y1(t-1)'}
{'y1(t-2)'}
{'y1(t-3)'}
{'y1(t-4)'}
{'u1(t-1)'}
{'u1(t-2)'}
{'u1(t-3)'}
{'u1(t-4)'}
Сравните выход модели с данными об оценке.
compare(z,sys)

Создайте время и массивы данных.
dt = 0.01; t = 0:dt:10; y = 10*sin(2*pi*t)+rand(size(t));
Создайте iddata объект без входного сигнала задан.
z = iddata(y',[],dt);
Оцените нелинейную модель ARX.
sys = nlarx(z,2)
sys = Nonlinear time series model Outputs: y1 Regressors: Linear regressors in variables y1 List of all regressors Output function: Wavelet Network with 8 units Sample time: 0.01 seconds Status: Estimated using NLARX on time domain data "z". Fit to estimation data: 92.92% (prediction focus) FPE: 0.2568, MSE: 0.2507
Оцените нелинейную модель ARX, которая использует функцию отображения sigmoidnet как его выходная функция.
Загрузите данные и разделите их на наборы данных оценки и валидации ze и zv.
load twotankdata.mat u y z = iddata(y,u,'Ts',0.2); ze = z(1:1500); zv = z(1501:end);
Сконфигурируйте sigmoidnet отображение функции. Зафиксируйте смещение к 0,2 и количество модулей к 15.
s = sigmoidnet; s.Offset.Value = 0.2; s. NonlinearFcn.NumberOfUnits = 15;
Создайте линейную спецификацию регрессора модели, которая содержит четыре выходных регрессора и пять входных регрессоров.
reg1 = linearRegressor({'y1','u1'},{1:4,0:4});Создайте полиномиальную спецификацию регрессора модели, которая содержит квадраты двух входных условий и трех выходных условий.
reg2 = polynomialRegressor({'y1','u1'},{1:2,0:2},2);Установите опции оценки для метода поиска и максимального количества итераций.
opt = nlarxOptions('SearchMethod','fmincon')'; opt.SearchOptions.MaxIterations = 40;
Оцените нелинейную модель ARX.
sys = nlarx(ze,[reg1;reg2],s,opt);
Подтвердите sys путем сравнения симулированного ответа модели на набор данных валидации.
compare(zv,sys)

Оцените линейную модель и улучшите модель путем добавления treepartition выходная функция.
Загрузите данные об оценке.
load throttledata ThrottleData
Оцените линейную модель ARX linsys с порядками [2 2 1].
linsys = arx(ThrottleData,[2 2 1]);
Создайте idnlarx обработайте по шаблону модель, которая использует linsys и задает sigmoidnet как выходная функция.
sys0 = idnlarx(linsys,treepartition);
Зафиксируйте линейный компонент sys0 так, чтобы во время оценки, линейного фрагмента sys0 остается идентичным linsys.
sys0.OutputFcn.LinearFcn.Free = false;
Оцените свободные параметры sys0, которые являются нелинейными параметрами функции и смещением.
sys = nlarx(ThrottleData,sys0);
Сравните подходящую точность для линейных и нелинейных моделей.
compare(ThrottleData,linsys,sys)

Генерация пользовательского объекта отображения сети требует определения пользовательской модульной функции.
Задайте модуль, функционируют и сохраняют его как gaussunit.m.
% Copyright 2015 The MathWorks, Inc. function [f, g, a] = gaussunit(x) f = exp(-x.*x); if nargout>1 g = -2*x.*f; a = 0.2; end
Создайте пользовательский объект отображения сети использование указателя на gaussunit функция.
H = @gaussunit; CNet = customnet(H);
Загрузите данные об оценке.
load iddata1;
Оцените нелинейную модель ARX с помощью пользовательской сети.
sys = nlarx(z1,[1 2 1],CNet)
sys = <strong>Nonlinear ARX model with 1 output and 1 input</strong> Inputs: u1 Outputs: y1 Regressors: Linear regressors in variables y1, u1 Output function: Custom Network with 10 units Sample time: 0.1 seconds Status: Estimated using NLARX on time domain data "z1". Fit to estimation data: 64.35% (prediction focus) FPE: 3.58, MSE: 2.465
Загрузите данные об оценке.
load motorizedcamera;Создайте iddata объект.
z = iddata(y,u,0.02,'Name','Motorized Camera','TimeUnit','s');
z iddata объект с шестью входными параметрами и двумя выходными параметрами.
Задайте порядки модели.
Orders = [ones(2,2),2*ones(2,6),ones(2,6)];
Задайте различные функции отображения для каждого выходного канала.
NL = [wavenet('NumberOfUnits',2),linear];Оцените нелинейную модель ARX.
sys = nlarx(z,Orders,NL)
sys = Nonlinear ARX model with 2 outputs and 6 inputs Inputs: u1, u2, u3, u4, u5, u6 Outputs: y1, y2 Regressors: Linear regressors in variables y1, y2, u1, u2, u3, u4, u5, u6 List of all regressors Output functions: Output 1: Wavelet Network with 2 units Output 2: Linear Function Sample time: 0.02 seconds Status: Estimated using NLARX on time domain data "Motorized Camera". Fit to estimation data: [98.72;98.77]% (prediction focus) FPE: 0.5719, MSE: 1.061
Загрузите данные об оценке и создайте iddata объект zZ содержит два выходных канала и шесть входных каналов.
load motorizedcamera;
z = iddata(y,u,0.02);Задайте набор линейных регрессоров, который использует выход и входные имена от z и содержит:
2 выходных регрессора с 1 задержкой.
6 входных пар регрессора с 1 и 2 задержками.
names = [z.OutputName; z.InputName];
lags = {1,1,[1,2],[1,2],[1,2],[1,2],[1,2],[1,2]};
reg = linearRegressor(names,lags);Оцените нелинейную модель ARX с помощью sigmoidnet отображение функции с четырьмя модулями для всех выходных каналов.
sys = nlarx(z,reg,sigmoidnet(4))
sys = Nonlinear ARX model with 2 outputs and 6 inputs Inputs: u1, u2, u3, u4, u5, u6 Outputs: y1, y2 Regressors: Linear regressors in variables y1, y2, u1, u2, u3, u4, u5, u6 List of all regressors Output functions: Output 1: Sigmoid Network with 4 units Output 2: Sigmoid Network with 4 units Sample time: 0.02 seconds Status: Estimated using NLARX on time domain data "z". Fit to estimation data: [98.86;98.79]% (prediction focus) FPE: 2.641, MSE: 0.9233
Загрузите данные об оценке z1, который имеет вход того и один выход, и получите выход и введите имена.
load iddata1 z1; names = [z1.OutputName z1.InputName]
names = 1×2 cell
{'y1'} {'u1'}
Задайте L как набор линейных регрессоров, который представляет , , и .
L = linearRegressor(names,{1,[2 5]});Задайте P как полиномиальный регрессор .
P = polynomialRegressor(names(1),1,2);
Задайте C как пользовательский регрессор . Используйте указатель анонимной функции, чтобы задать эту функцию.
C = customRegressor(names,{2 3},@(x,y)x.*y)C =
Custom regressor: y1(t-2).*u1(t-3)
VariablesToRegressorFcn: @(x,y)x.*y
Variables: {'y1' 'u1'}
Lags: {[2] [3]}
Vectorized: 1
TimeVariable: 't'
Regressors described by this set
Объедините регрессоры в вектор-столбце R.
R = [L;P;C]
R=3×1 object
[3 1] array of linearRegressor, polynomialRegressor, customRegressor objects.
------------------------------------
1. Linear regressors in variables y1, u1
Variables: {'y1' 'u1'}
Lags: {[1] [2 5]}
UseAbsolute: [0 0]
TimeVariable: 't'
------------------------------------
2. Order 2 regressors in variables y1
Order: 2
Variables: {'y1'}
Lags: {[1]}
UseAbsolute: 0
AllowVariableMix: 0
AllowLagMix: 0
TimeVariable: 't'
------------------------------------
3. Custom regressor: y1(t-2).*u1(t-3)
VariablesToRegressorFcn: @(x,y)x.*y
Variables: {'y1' 'u1'}
Lags: {[2] [3]}
Vectorized: 1
TimeVariable: 't'
Regressors described by this set
Оцените нелинейную модель ARX с R.
sys = nlarx(z1,R)
sys = Nonlinear ARX model with 1 output and 1 input Inputs: u1 Outputs: y1 Regressors: 1. Linear regressors in variables y1, u1 2. Order 2 regressors in variables y1 3. Custom regressor: y1(t-2).*u1(t-3) List of all regressors Output function: Wavelet Network with 1 unit Sample time: 0.1 seconds Status: Estimated using NLARX on time domain data "z1". Fit to estimation data: 59.73% (prediction focus) FPE: 3.356, MSE: 3.147
Просмотрите полный набор регрессора.
getreg(sys)
ans = 5×1 cell
{'y1(t-1)' }
{'u1(t-2)' }
{'u1(t-5)' }
{'y1(t-1)^2' }
{'y1(t-2).*u1(t-3)'}
Загрузите данные об оценке.
load iddata1;Создайте сигмоидальный объект отображения сети с 10 модулями и никаким линейным членом.
SN = sigmoidnet(10,false);
Оцените нелинейную модель ARX. Подтвердите, что модель не использует линейную функцию.
sys = nlarx(z1,[2 2 1],SN); sys.OutputFcn.LinearFcn.Use
ans = logical
0
Загрузите данные об оценке.
load throttledata;Детрендируйте данные.
Tr = getTrend(ThrottleData); Tr.OutputOffset = 15; DetrendedData = detrend(ThrottleData,Tr);
Оцените линейную модель ARX.
LinearModel = arx(DetrendedData,[2 1 1]);
Оцените нелинейную модель ARX с помощью линейной модели. Порядки модели, задержки и линейные параметры NonlinearModel выведены из LinearModel.
NonlinearModel = nlarx(ThrottleData,LinearModel)
NonlinearModel = Nonlinear ARX model with 1 output and 1 input Inputs: Step Command Outputs: Throttle Valve Position Regressors: Linear regressors in variables Throttle Valve Position, Step Command List of all regressors Output function: Wavelet Network with 7 units Sample time: 0.01 seconds Status: Estimated using NLARX on time domain data "ThrottleData". Fit to estimation data: 99.03% (prediction focus) FPE: 0.1127, MSE: 0.1039
idnlarx ОбъектЗагрузите данные об оценке.
load iddata1;Создайте idnlarx модель.
sys = idnlarx([2 2 1]);
Сконфигурируйте модель с помощью записи через точку для:
Используйте сигмоидальный объект отображения сети.
Присвойте имя.
sys.Nonlinearity = 'sigmoidnet'; sys.Name = 'Model 1';
Оцените нелинейную модель ARX со структурой и свойствами, заданными в idnlarx объект.
sys = nlarx(z1,sys)
sys = Nonlinear ARX model with 1 output and 1 input Inputs: u1 Outputs: y1 Regressors: Linear regressors in variables y1, u1 List of all regressors Output function: Sigmoid Network with 10 units Name: Model 1 Sample time: 0.1 seconds Status: Estimated using NLARX on time domain data "z1". Fit to estimation data: 69.03% (prediction focus) FPE: 2.918, MSE: 1.86
Если оценка останавливается в локальном минимуме, можно встревожить модель с помощью init и повторно оцените модель.
Загрузите данные об оценке.
load iddata1;Оцените первоначальную нелинейную модель.
sys1 = nlarx(z1,[4 2 1],'sigmoidnet');Случайным образом встревожьте параметры модели, чтобы избежать локальных минимумов.
sys2 = init(sys1);
Оцените новую нелинейную модель со встревоженными значениями.
sys2 = nlarx(z1,sys1);
Загрузите данные об оценке.
load twotankdata;Создайте iddata объект из данных об оценке.
z = iddata(y,u,0.2);
Создайте nlarxOptions набор опции, задающий ошибочную цель минимизации симуляции и максимум 50 итераций оценки.
opt = nlarxOptions;
opt.Focus = 'simulation';
opt.SearchOptions.MaxIterations = 50;Оцените нелинейную модель ARX.
sys = nlarx(z,[4 4 1],'sigmoidnet',opt)sys = Nonlinear ARX model with 1 output and 1 input Inputs: u1 Outputs: y1 Regressors: Linear regressors in variables y1, u1 List of all regressors Output function: Sigmoid Network with 10 units Sample time: 0.2 seconds Status: Estimated using NLARX on time domain data "z". Fit to estimation data: 88.79% (simulation focus) FPE: 3.341e-05, MSE: 0.0004307
Загрузите данные о регуляризации в качестве примера.
load regularizationExampleData.mat nldata;
Создайте sigmoidnet отображение объекта с 30 модулями и задает порядки модели.
MO = sigmoidnet(30); Orders = [1 2 1];
Создайте набор опции оценки и установите метод поиска оценки для lm.
opt = nlarxOptions('SearchMethod','lm');
Оцените неупорядоченную модель.
sys = nlarx(nldata,Orders,MO,opt);
Сконфигурируйте регуляризацию Lambda параметр.
opt.Regularization.Lambda = 1e-8;
Оцените упорядоченную модель.
sysR = nlarx(nldata,Orders,MO,opt);
Сравните эти две модели.
compare(nldata,sys,sysR)

Большой отрицательный результат подгонки для неупорядоченной модели указывает на плохую подгонку к данным. Оценка упорядоченной модели приводит к значительно лучшему результату.
data — Данные об оценке временного интервалаiddata возразите | числовая матрицаДанные об оценке временного интервала в виде iddata возразите или числовая матрица.
Если data iddata объект, затем data может иметь один или несколько выходных каналов и нуля или более входных каналов.
Если data числовая матрица, затем количество столбцов данных должно совпадать с суммой количества входных параметров (nu) и количество выходных параметров (ny.
data должен быть однородно произведен и не может содержать то, чтобы избегать (NaNВыборки.
orders — Порядки модели ARXnlarx порядки [na nb nk]Модель ARX заказывает в виде матричного [na nb nk]нет данных обозначает количество задержанных выходных параметров, nb обозначает количество задержанных входных параметров и nk обозначает минимальную входную задержку. Минимальная выходная задержка фиксируется к 1. Для получения дополнительной информации о том, как создать orders матрица, смотрите arx.
Когда вы задаете orders, программное обеспечение преобразует информацию для заказа в линейную форму регрессора в idnlarx
Regressors свойство. Для примера смотрите, Создают Нелинейную Модель ARX Используя Порядки Модели ARX.
regressors — Спецификация регрессораlinearRegressor возразите | polynomialRegressor возразите | customRegressor возразите | массив столбца объектов спецификации регрессораСпецификация регрессора в виде вектор-столбца, содержащего один или несколько объектов спецификации регрессора, которые являются linearRegressor объекты, polynomialRegressor объекты и customRegressor объекты. Каждый объект задает формулу для генерации регрессоров от изолированных переменных. Например:
L = linearRegressor({'y1','u1'},{1,[2 5]}) генерирует регрессоры y1 (t –1), u1 (t –2), и u2 (t –5).
P = polynomialRegressor('y2',4:7,2) генерирует регрессоры y2 (t –4) 2, y2 (t –5) 2, y2 (t –6) 2, и y2 (t –7) 2.
C = customRegressor({'y1','u1','u2'},{1 2 2},@(x,y,z)sin(x.*y+z)) генерирует один sin регрессора (y1 (t –1) u1 (t –2) +u2 (t –2)).
Когда вы создаете набор регрессора, чтобы поддержать оценку с iddata объект, можно использовать имена ввода и вывода объекта, а не создать имена для функции регрессора. Например, предположите, что вы создаете линейный регрессор для модели, планируете использовать iddata объект z оценить модель. Можно использовать следующую команду, чтобы создать линейный регрессор.
L = linearRegressor([z.outputName;z.inputName],{1,[2 5]})Для примера создания и использования SISO линейный набор регрессора, смотрите Оценку Нелинейная Модель ARX Используя Линейный Набор Регрессора. Для примера создания MIMO линейный набор регрессора, который получает имена переменных из набора данных оценки, видит Оценку MIMO Нелинейная Модель ARX с Той же Функцией Отображения для Всех Выходных параметров.
output_fcn Выходная функция'wavenet' (значение по умолчанию) | 'linear' | [] | '' | 'sigmoidnet' | 'treepartition' | 'neuralnet' | 'customnet' | отображение объекта | массив отображения объектовВыходная функция, которая сопоставляет регрессоры idnlarx модель в выход модели в виде массива столбца, содержащего нуль или больше следующих строк или объектов:
'wavenet' или wavenet объект | Сеть Wavelet |
'linear' или '' или [] или linear объект | Линейная функция |
'sigmoidnet' или sigmoidnet объект | Сигмоидальная сеть |
'treepartition' или treepartition объект | Модель регрессии раздела двоичного дерева |
neuralnet объект | Нейронная сеть — Сеть прямого распространения Deep Learning Toolbox™. |
customnet объект | Пользовательская сеть — Подобно sigmoidnet, но с пользовательской заменой для сигмоидальной функции. |
Используйте строку, такую как 'sigmoidnet', использовать свойства по умолчанию функционального объекта отображения. Используйте сам объект, такой как sigmoidnet, когда это необходимо, сконфигурировать свойства объекта отображения.
wavenet, sigmoidnet, treepartion, и customnet объекты содержат и линейные и нелинейные компоненты. Можно удалить (не, используют), линейные компоненты wavenet, sigmoidnet, и customnet путем установки LinearFcn.Use значение к false.
neuralnet функция имеет только нелинейный компонент, который является network Объект (Deep Learning Toolbox) Deep Learning Toolbox. Линейная функция, когда имя подразумевает, имеет только линейный компонент.
output_fcn является статическим в этом, это зависит только от значений данных в определенное время, но не непосредственно вовремя его. Например, если выходная функция y (t) равна y0 + a1
y (t –1) + a2
y (t –2) + … b1
u (t –1) + b2
u (t –2) + …, то output_fcn линейная функция что linear отображение объекта представляет.
Определение вектора символов, например, 'sigmoidnet', создает объект отображения с настройками по умолчанию. В качестве альтернативы можно задать свойства объектов отображения двумя способами:
Создайте объект отображения использование аргументов, чтобы изменить свойства по умолчанию.
MO = sigmoidnet(15);
Создайте отображение значения по умолчанию, возражают сначала и затем используют запись через точку, чтобы изменить свойства.
MO = sigmoidnet; MO.NumberOfUnits = 15;
Для ny каналы выхода можно задать объекты отображения индивидуально для каждого канала установкой output_fcn к массиву объектов отображения ny. Например, следующий код задает OutputFcn использование записи через точку для системы с двумя входными каналами и двумя выходными каналами.
sys = idnlarx({'y1','y2'},{'u1','u2'});
sys.OutputFcn = [wavenet; sigmoidnet];OutputFcn как вектор символов или один объект отображения.
output_fcn представляет статическую функцию отображения, которая преобразовывает регрессоры нелинейной модели ARX в выход модели. output_fcn является статическим, потому что это не зависит вовремя. Например, если , затем output_fcn линейная функция, представленная linear объект.
Для примера определения выходной функции смотрите, Задают и Настраивают Выходную функцию.
linmodel — Дискретное время линейная модельidpoly объект | idss объект | idtf объект | idproc объектsys0 — Нелинейная модель ARXidnlarx модельНелинейная модель ARX в виде idnlarx модель. sys0 может быть:
Модель ранее оценила использование nlarx. Алгоритм оценки использует параметры sys0 как исходные предположения. В этом случае использовать init немного встревожить свойства модели постараться не захватывать модель в локальных минимумах.
sys = init(sys); sys = nlarx(data,sys);
Модель ранее создала использование idnlarx конструктор и с набором свойств с помощью записи через точку. Например, используйте следующее, чтобы создать объект idnlarx, установить его свойства и оценить модель.
sys1 = idnlarx('y1','u1',Regressors); sys1.OutputFcn = 'treepartition'; sys1.Ts = 0.02; sys1.TimeUnit = 'Minutes'; sys1.InputName = 'My Data'; sys2 = nlarx(data,sys1);
Предыдущий код эквивалентен следующей nlarx команде.
sys2 = nlarx(data,Regressors,'treepartition','Ts',0.02,'TimeUnit','Minutes', ... 'InputName','My Data');
Options — Опции оценкиnlarxOptions опция установленаОпции оценки для нелинейной идентификации модели ARX в виде nlarxOptions опция установлена.
sys — Нелинейная модель ARXidnlarx объектНелинейная модель ARX, которая соответствует данным данным об оценке, возвратилась как idnlarx объект. Эта модель создается с помощью заданных порядков модели, средства оценки нелинейности и опций оценки.
Информация о результатах оценки и используемых опциях хранится в Report свойство модели. Содержимое Report зависьте от выбора нелинейности, и оценка фокусируют вас заданный для nlarx. Report имеет следующие поля:
| Сообщите о поле | Описание | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Status | Сводные данные состояния модели, которое указывает, была ли модель создана конструкцией или получена оценкой. | ||||||||||||||||||
Method | Команда оценки используется. | ||||||||||||||||||
Fit | Количественная оценка оценки, возвращенной как структура. Смотрите Функцию потерь и Метрики качества Модели для получения дополнительной информации об этих метриках качества. Структура имеет следующие поля:
| ||||||||||||||||||
Parameters | Ориентировочные стоимости параметров модели. | ||||||||||||||||||
OptionsUsed | Набор опции используется для оценки. Если никакие пользовательские опции не были сконфигурированы, это - набор опций по умолчанию. Смотрите | ||||||||||||||||||
RandState | Состояние потока случайных чисел в начале оценки. | ||||||||||||||||||
DataUsed | Атрибуты данных используются для оценки, возвращенной как структура со следующими полями:
| ||||||||||||||||||
Termination | Условия завершения для итеративного поиска, используемого для ошибочной минимизации предсказания, возвращенной как структура со следующими полями:
Для методов оценки, которые не требуют числовой оптимизации поиска, |
Для получения дополнительной информации об использовании Report, см. Отчет Оценки.
Нелинейная модель ARX состоит из регрессоров модели и выходной функции. Выходная функция включает линейные и нелинейные функции, которые действуют на регрессоры модели, чтобы дать выход модели и фиксированное смещение для того выхода. Эта блок-схема представляет структуру нелинейной модели ARX в сценарии симуляции.
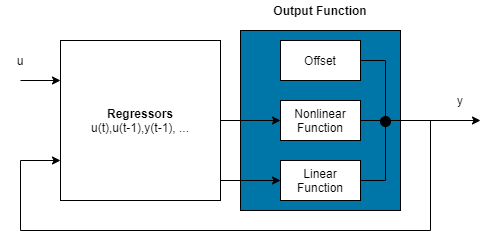
Программное обеспечение вычисляет нелинейную модель ARX выход y на двух этапах:
Это вычисляет значения регрессора из текущих и прошлых входных значений и прошлых выходных данных.
В самом простом случае регрессоры являются задержанными вводами и выводами, такими как u (t –1) и y (t –3). Подобные регрессоры называются linear regressors. Вы задаете линейные регрессоры с помощью linearRegressor объект. Можно также задать линейные регрессоры при помощи линейных порядков модели ARX как входной параметр. Для получения дополнительной информации смотрите Нелинейные Порядки Модели ARX и Задержку. Однако этот второй подход ограничивает ваш набор регрессора к линейным регрессорам с последовательными задержками. Чтобы создать polynomial regressors, используйте polynomialRegressor объект. Можно также задать custom regressors, которые являются нелинейными функциями задержанных вводов и выводов. Например, u (t –1) y (t –3) является пользовательским регрессором, который умножает экземпляры ввода и вывода вместе. Задайте пользовательские регрессоры с помощью customRegressor объект.
Можно присвоить любой из регрессоров как входные параметры с блоком линейной функции выходной функции, нелинейного функционального блока или обоих.
Это сопоставляет регрессоры с выходом модели с помощью блока выходной функции. Блок выходной функции может включать линейные и нелинейные блоки параллельно. Например, рассмотрите следующее уравнение:
Здесь, x является вектором из регрессоров, и r является средним значением x. выход блока линейной функции. представляет выход нелинейного функционального блока. Q является матрицей проекции, которая делает вычисления хорошо подготовленными. d является скалярным смещением, которое добавляется к объединенным выходным параметрам линейных и нелинейных блоков. Точная форма F (x) зависит от вашего выбора выходной функции. Можно выбрать из доступных объектов отображения, таких как сети древовидного раздела, сети вейвлета и многоуровневые нейронные сети. Можно также исключить или линейное или нелинейный функциональный блок от выходной функции.
При оценке нелинейной модели ARX программное обеспечение вычисляет значения параметра модели, такие как L, r, d, Q и другие параметры, задающие g.
Получившиеся нелинейные модели ARX idnlarx объекты, которые хранят все данные модели, включая регрессоры модели и параметры выходной функции. Для получения дополнительной информации об этих объектах, смотрите Нелинейные Структуры модели.
idnlarx свойства не рекомендуются.Не рекомендуемый запуск в R2021a
Запуск в R2021a, нескольких свойствах idnlarx были изменены или заменены.
Эти изменения влияют на синтаксисы в обоих idnlarx и nlarx. Использованию pre-R2021a свойств в следующей таблице препятствуют. Однако программное обеспечение все еще принимает синтаксисы вызова, которые включают эти свойства. Нет никаких планов исключить эти синтаксисы в это время. Синтаксис команд, который использует порядки модели ARX, продолжается быть рекомендуемым синтаксисом.
| Свойство Pre-R2021a | Свойство R2021a | Использование |
|---|---|---|
Модель ARX заказывает na,nb,nk | Regressors, который может включать linearRegressor, polynomialRegressor, и customRegressor объекты. |
Вы можете значения более не заявки на изменение в существующем |
customRegressors | Regressors | Используйте polynomialRegressor или customRegressor создать объекты регрессора и добавить объекты в Regressors массив. |
NonlinearRegressors | RegressorUsage | RegressorUsage таблица, которая содержит присвоения регрессора на линейные и нелинейные выходные компоненты. Измените присвоения путем изменения соответствующего RegressorUsageзаписи таблицы. |
Nonlinearity | OutputFcn | Изменение только номинально. Свойство остается объект или массив или возражает, что регрессор карты вводит к выходу. |
Поддержка параллельных вычислений доступна для оценки с помощью lsqnonlin метод поиска (требует Optimization Toolbox™). Чтобы включить параллельные вычисления, использовать nlarxOptions, установите SearchMethod к 'lsqnonlin', и набор SearchOptions.Advanced.UseParallel к true, как в следующем примере.
opt = nlarxOptions;
opt.SearchMethod = 'lsqnonlin';
opt.SearchOptions.Advanced.UseParallel = true;
aic | fpe | goodnessOfFit | idnlarx | isnlarx | linearRegressor | nlarxOptions | polynomialRegressor
У вас есть модифицированная версия этого примера. Вы хотите открыть этот пример со своими редактированиями?
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.